
- •Лекция 1. Метод математической индукции.
- •Принцип индукции.
- •Неравенство Коши-Буняковского.
- •Лекция 2. Комбинаторика.
- •Принцип умножения.
- •Перестановки.
- •Размещения.
- •Рассмотрим первый набор чисел.
- •Сочетания.
- •Некоторые свойства биномиальных коэффициентов:
- •Перестановки с повторениями.
- •Сочетания с повторениями.
- •Бином Ньютона.
- •1). База индукции.
- •2). Индуктивное предположение.
- •3). Индуктивный переход.
- •Лекция 3. Введение в теорию множеств. Понятия о множестве.
- •Два основных интуитивных принципа наивной теории множеств.
- •Интуитивный принцип объемности.
- •Интуитивный принцип абстракции.
- •Парадокс Рассела.
- •Лекция 4. Операции над множествами. Сравнение множеств.
- •Свойства отношения включения.
- •Операции над множествами.
- •Лекция 5. Свойства операций над множествами.
- •Формула включения и исключения.
- •Лекция 6.
- •Упорядоченные пары.
- •Прямое произведение множеств.
- •Бинарные отношения.
- •Композиция отношений.
- •Теорема о свойствах бинарного отношения.
- •Матрицы конечных бинарных отношений.
- •Свойства матриц конечных бинарных отношений.
- •Матрицы объединения и пересечения двух бинарных отношений.
- •Матрица композиции двух конечных бинарных отношений.
- •Матрица обратного отношения.
- •Матрица рефлексивного бинарного отношения
- •Ядро бинарного отношения.
- •Свойства ядра:
- •Лекция 8. Отношения эквивалентности.
- •Классы эквивалентности.
- •Функции.
- •Инъекции и биекции.
- •Примеры экзаменационных задач.
- •Лекция 9. Композиция функций.
- •Ядро функции).
- •Отношения порядка.
- •Экстремальные элементы в упорядоченном множестве.
- •Лекция 10. Верхняя и нижняя грани частично упорядоченного множества.
- •Решетки.
- •Ограниченные решетки.
- •Решетки с дополнением.
- •Частичный порядок в решетке.
- •Лекция 11. Матроиды.
- •Максимально независимые подмножества.
- •Алгоритм построения базы матроида.
- •Ранг множества.
- •Жадный алгоритм.
Алгоритм построения базы матроида.
Следующий алгоритм строит базу в матроиде М (Е, ).
-
Произвольно упорядочить элементы множества Е, Е = (е1, е2,..., еn);
-
Включить элемент e1 в В;
-
Для i =
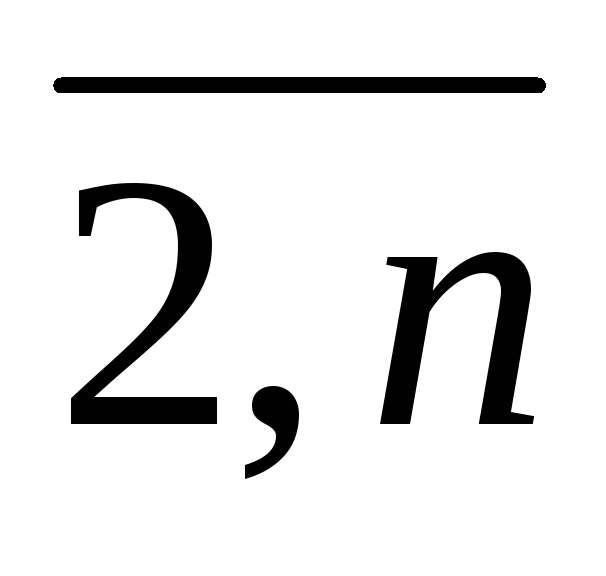 .
Если В{ei},
то положить В = В{ei},
иначе
.
Если В{ei},
то положить В = В{ei},
иначе
пропустить ei.
Обоснование алгоритма.
-
Алгоритм строит независимое множество B. Обозначим |B|=k.
-
Допустим, что построенное независимое множество В, не является базой матроида. Пусть А = {а1, ... , аm} – база матроида
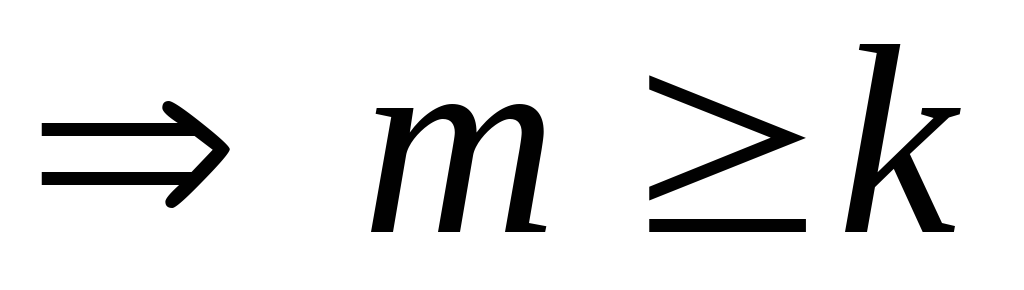 .
По М.3:(
.
По М.3:(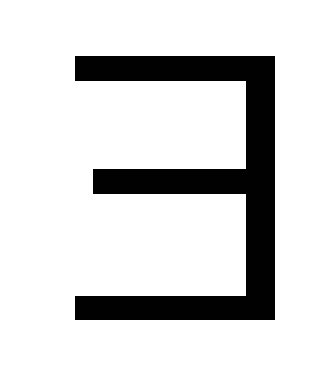 ei
ei
 А\В): В
А\В): В {ei}.
По M.2:{ei}
{ei}.
По M.2:{ei} (любое
подмножество В) .
Но алгоритм просматривает все элементы
ei,
и на некотором этапе он отбросил элемент
ei
, как неподходящий. Противоречие.
(любое
подмножество В) .
Но алгоритм просматривает все элементы
ei,
и на некотором этапе он отбросил элемент
ei
, как неподходящий. Противоречие.
Ранг множества.
Рангом множества X E называется мощность его баз. Определение корректно, так как все базы равномощны.
r(x)
= |A|, A![]() .
.
Теорема.
r(x) = |X| X.
Доказательство.
-
Пусть X r(x) = |X|;
-
Пусть r(x) = |X|, но у всякого множества X есть единственное подмножество (оно само), равномощное X
 .
.
Теорема (о рангах).
Пусть А, В Е и е1, е2 Е.
r.1: 0 r(A) |A|; – очевидно.
r.2: Если В А, то r(B) r(A); – очевидно;
r.3: r(A) r(A{ei}) r(A) + 1; – очевидно;
r.4: r(AB) + r(AB) r(A) + r(B).
Доказательство.
Пусть r(AB) = i и С AB, C = {c1, ... ,ci}.
Дополним множество С, если необходимо, элементами множества А до
базы множества А, обозначим это
множество через D
![]() ,
пусть
,
пусть
D = {c1, c2, ..., ci, d1, d2, ..., dj}, r(A) = i + j.
Дополним множество D, если необходимо, элементами множества B до базы множества А B, обозначим это множество через F, F А B. Пусть
F = {c1, c2, ..., ci, d1, d2, ..., dj, f1, f2, ...,fk}, r(AB) = i + j + k.
Пусть F1 = {c1, c2, ..., ci, f1, f2, ...,fk}, F1F, F1B. Тогда по М.2, F1 F1 либо база множества В, либо F1 можно расширить до базы В r(B) i + k,
r(AB) + r(AB) = (i + j + k) + i = (i + j) + (i + k) r(A) + r(B).
r.5: Если r(A{e1}) = r(A{e2}) = r(A), то r(A{e1 ,e2}) = r(A)
Доказательство.
A{e1, e2} = [A{e1}] [A{e2}] [A{e1}] [A{e2}] = А
r(A{e1, e2}) r(A{e1}) + r(A{e2}) – r(A) = r(A) + r(A) - r(A) = r(A).
С другой стороны, r(A{e1, e2}) r(A) r(A{e1, e2}) = r(A).
Теорема доказана.
Жадный алгоритм.
Пусть имеются конечное множество Е и
семейство
его подмножеств, причем все одноэлементные
подмножества множества Е принадлежат
семейству .
Пусть каждому элементу е из Е
поставлено в соответствие число (е)
> 0, называемое весом
е. Тем самым, задается весовая
функция W: ER+.
Весом подмножества X
называется сумма весов элементов этого
подмножества, W(x)
=
![]() (е),
eX.
(е),
eX.
Задача. Среди всех множеств семейства отыскать множество наибольшего веса.
Жадный алгоритм решает эту задачу следующим образом:
-
Упорядочить элементы Е в порядке убывания их весов:
(е1) (е2) ... (еn).
-
Включить e1 в множество Х, которое строит алгоритм.
-
Для i =
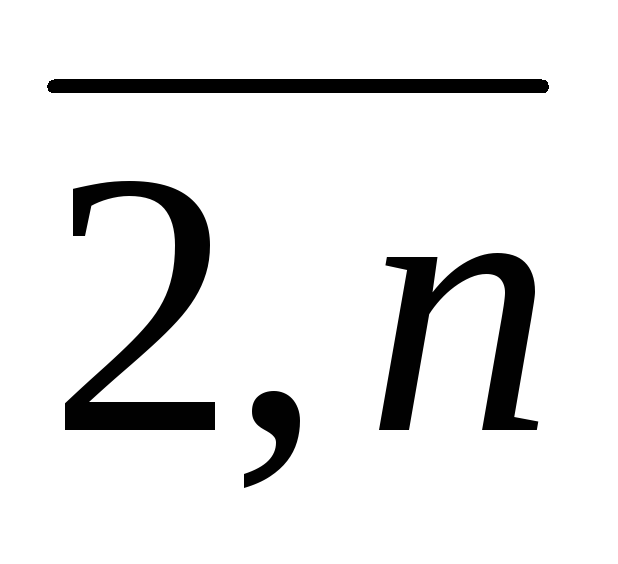 :
если X
{ei},
включить еi
в Х, иначе пропустить ei.
:
если X
{ei},
включить еi
в Х, иначе пропустить ei.
Алгоритм быстрый и эффективный.
Вопрос: Всегда ли построенное множество Х имеет максимальный вес?
Оказывается, что если пара (Е, ) образует матроид, то жадный алгоритм обязательно строит множество Х с максимальным весом, иначе он может ошибаться.
Прежде чем доказать эту теорему, рассмотрим конкретный пример
работы жадного алгоритма. Сразу заметим, что если (Е, ) – матроид, то жадный алгоритм строит его базу, так как он работает в точности как описанный нами ранее алгоритм построения базы матроида.
В качестве примера рассмотрим матрицу:
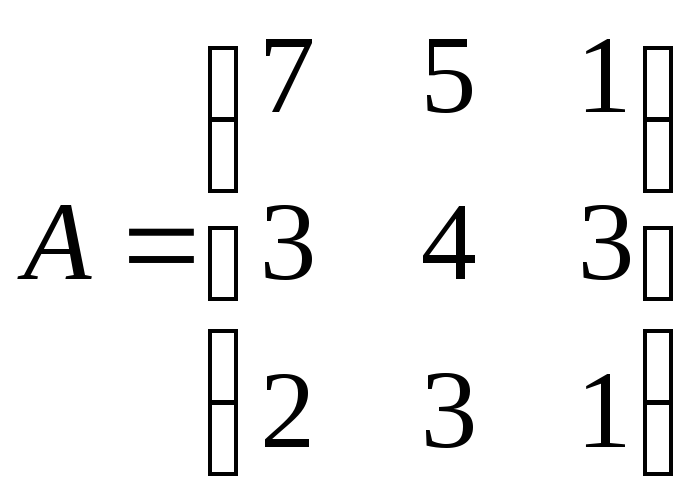
Задача 1. Нужно выбрать 3 числа по одному из каждого столбца, чтобы их сумма была максимальной. Здесь Е – множество из 9 элементов матрицы А. Семейство образуют всевозможные тройки чисел, взятых по одному из каждого столбца матрицы А; различные двойки чисел, выбранных из разных столбцов матрицы А; отдельные элементы матрицы А; пустое множество. Система (Е,) – образует матроид разбиения.
Расположим элементы матрицы А в порядке убывания. Под ними запишем их координаты (номера строки и столбца, в которых они лежат). Обведем в кружок те элементы, которые выберет жадный алгоритм.



4 3 3 2 1 1
(1, 1) (1, 2) (2, 2) (2, 3) (2, 1) (3, 2) (3, 1) (1, 3) (3, 3)
Жадный алгоритм правильно решил поставленную задачу.
Задача 2. Из этой же матрицы А нужно выбрать три числа, по одному из каждой строки и столбца. Тогда система – это тройки чисел, лежащие в разных строках и столбцах матрицы А; двойки чисел, лежащие в разных строках и столбцах матрицы А; отдельные элементы матрицы А; пустое множество. Система (Е,) не образует матроид, вследствие нарушения правила М.3. Действительно, если, например взять А1 = {a13 , a21}, B = {a12, a23, a31}, то А1, B , | B |=| А1| + 1, но (ai j B): А1{ai j }.
Жадный алгоритм выберет такие элементы из А (обведены кружком):
3 3



5 3 2 1
(1 ,1) (1, 2) (2, 2) (2, 3) (2, 1) (3, 2) (3, 1) (1, 3) (3, 3)
Верное решение представлено числами, обведенными в квадрат.
7 + 3 + 3 = 13 > 7 + 4 + 1 = 12.
Теорема.
Если пара (Е, ) образует матроид, то жадный алгоритм строит множество с максимальным весом. В противном случае жадный алгоритм может ошибаться.
Доказательство.
Пусть (Е,) – матроид и Х = {x1, x2, ..., xm} – множество, которое строит алгоритм. Положим, что элементы множества Х упорядочены в порядке убывания весов (заданы в том порядке, в котором их выбирает жадный алгоритм): w(x1) w(x2) ... w(xm).
Множество Х – база матроида,
![]() ,
поэтому мощность любого другого
независимого множества Y
меньше мощности множества Х.
,
поэтому мощность любого другого
независимого множества Y
меньше мощности множества Х.
Пусть Y = {y1, y2, ..., yk} – другое независимое множество. Положим, что его элементы также расположены в порядке убывания весов:
w(y1)
w(y2)
...
w(yk).
При этом k
m. Покажем, что
w(xi)
w(yi),
для всех
![]() .
Заметим, что w(x1)
w(y1).
Пусть i – самый
маленький номер такой, что w(yi)
> w(xi).
.
Заметим, что w(x1)
w(y1).
Пусть i – самый
маленький номер такой, что w(yi)
> w(xi).
Рассмотрим два независимых множества:
А = {x1, x2, ..., xi-1} и В = {y1, y2, ..., yi}
По аксиоме М.2.: |B|=
|A| + 1
(![]() yjB\A):
A1={x1,
x2,
..., xi-1,yj}.
yjB\A):
A1={x1,
x2,
..., xi-1,yj}.
Но j i, тогда w(yj) w(yi) > w(xi).
Поэтому жадный алгоритм должен был включить на i – ом шаге в множество Х элемент yj вместо элемента xi или на шаге с номером, меньшим i, включить элемент yj во множество Х – противоречие.
Покажем, как может ошибаться жадный алгоритм, если нарушены аксиомы М.2. и М.3. матроида.
Случай 1. Нарушена аксиома М.2.
Тогда
![]()
![]() .
Рассмотрим такую весовую функцию
.
Рассмотрим такую весовую функцию
![]()
![]()
Значит, w(B) = w(A) и B.
Жадный алгоритм сначала просмотрит все элементы А, но не сможет целиком включить их в множество Х, которое он строит, так как A. В результате w(Х) < w(B) и алгоритм не найдет множество В с большим весом.
Случай 2. Нарушено условие М.3., аксиому М.2. считаем выполненной.
Тогда
![]() )
)
Заметим, что не может выполняться
включение А В.
Ведь, если А
В, то, в следствие справедливости
М.2.:
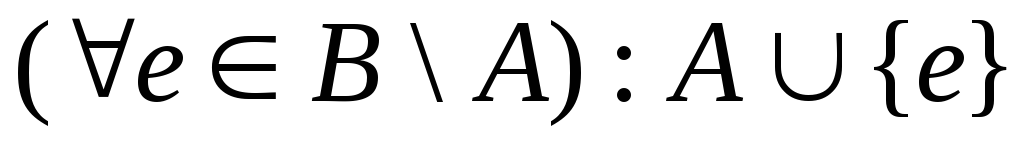 В
В
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Рассмотрим такую весовую функцию:
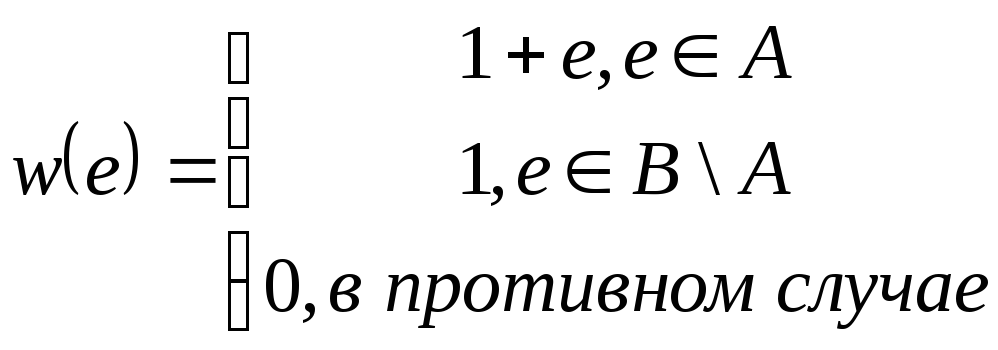
Число выберем
из условия 0 < ![]() .
Жадный алгоритм сначала просмотрит
все элементы множества А и включит
их в множество Х. Затем он просмотрит
все элементы множества В\А и ни один
из них не сможет включить в множество
Х. В результате алгоритм построит
множество Х вес которого равен весу
множества А:
.
Жадный алгоритм сначала просмотрит
все элементы множества А и включит
их в множество Х. Затем он просмотрит
все элементы множества В\А и ни один
из них не сможет включить в множество
Х. В результате алгоритм построит
множество Х вес которого равен весу
множества А:
![]() ).
).
Покажем, что множество В имеет больший вес:
B = (AB) (B\A);
w(B) = w(AB)w(B\A) = p(1+) + (k + 1 – p)1;
w(B) – w(A) = 1– (k – p)>0
Теорема доказана.
