
- •Лекция 1. Метод математической индукции.
- •Принцип индукции.
- •Неравенство Коши-Буняковского.
- •Лекция 2. Комбинаторика.
- •Принцип умножения.
- •Перестановки.
- •Размещения.
- •Рассмотрим первый набор чисел.
- •Сочетания.
- •Некоторые свойства биномиальных коэффициентов:
- •Перестановки с повторениями.
- •Сочетания с повторениями.
- •Бином Ньютона.
- •1). База индукции.
- •2). Индуктивное предположение.
- •3). Индуктивный переход.
- •Лекция 3. Введение в теорию множеств. Понятия о множестве.
- •Два основных интуитивных принципа наивной теории множеств.
- •Интуитивный принцип объемности.
- •Интуитивный принцип абстракции.
- •Парадокс Рассела.
- •Лекция 4. Операции над множествами. Сравнение множеств.
- •Свойства отношения включения.
- •Операции над множествами.
- •Лекция 5. Свойства операций над множествами.
- •Формула включения и исключения.
- •Лекция 6.
- •Упорядоченные пары.
- •Прямое произведение множеств.
- •Бинарные отношения.
- •Композиция отношений.
- •Теорема о свойствах бинарного отношения.
- •Матрицы конечных бинарных отношений.
- •Свойства матриц конечных бинарных отношений.
- •Матрицы объединения и пересечения двух бинарных отношений.
- •Матрица композиции двух конечных бинарных отношений.
- •Матрица обратного отношения.
- •Матрица рефлексивного бинарного отношения
- •Ядро бинарного отношения.
- •Свойства ядра:
- •Лекция 8. Отношения эквивалентности.
- •Классы эквивалентности.
- •Функции.
- •Инъекции и биекции.
- •Примеры экзаменационных задач.
- •Лекция 9. Композиция функций.
- •Ядро функции).
- •Отношения порядка.
- •Экстремальные элементы в упорядоченном множестве.
- •Лекция 10. Верхняя и нижняя грани частично упорядоченного множества.
- •Решетки.
- •Ограниченные решетки.
- •Решетки с дополнением.
- •Частичный порядок в решетке.
- •Лекция 11. Матроиды.
- •Максимально независимые подмножества.
- •Алгоритм построения базы матроида.
- •Ранг множества.
- •Жадный алгоритм.
Примеры экзаменационных задач.
-
Пусть X, Y – два множества, состоящие из n и m элементов соответственно. Какова мощность множества всех тотальных функций, определенных на X, со значением в Y?
Решение.
Чтобы задать любую тотальную функцию нужно выполнить n действий: указать образ каждого элемента множества X, но каждое действие можно выполнить m способами число функций равно mn.
-
Доказать, что
 ,
f : XY,
A, B
X.
,
f : XY,
A, B
X.
Доказательство.
Пусть
![]() или
или
![]() или
или
![]() .
.
Пусть
![]() или
или
![]()
![]() .
.
-
Доказать, что
 ,
y = f(x),
A, B
Y,
,
y = f(x),
A, B
Y,
 – не обязательно функция.
– не обязательно функция.
Доказательство.
-
Пусть
 и
и
 и
и
 .
. -
Пусть
 и
и
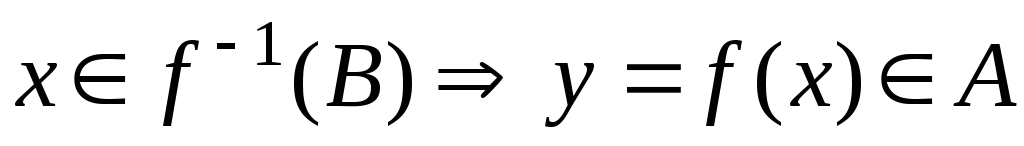 и
и
 .
. -

Лекция 9. Композиция функций.
Т.к. всякая функция – это бинарное отношение, то мы можем строить композицию функций, как композицию бинарных отношений. Если
f: X
Z , то z
= f(x).
Если g: Z
Y, то y
= g(z),
тогда f![]() g:
X
Y .
g:
X
Y .
Композиция функций f![]() g
= {(x, y)|
xX,
yY,
(
g
= {(x, y)|
xX,
yY,
(![]() zZ):
(x, z)
f и
zZ):
(x, z)
f и
(z, y)
g} = {(x,
y)| (![]() z):
z = f(x)
и y = g(z)}
= {(x, y)|
y = g(f(x))}.
z):
z = f(x)
и y = g(z)}
= {(x, y)|
y = g(f(x))}.
Композиция функций – это не просто бинарное отношение, это снова функция. Действительно, если элемент х задан, то z = f(x) определяется однозначно, тогда y = g(z) тоже определяется однозначно.
Пример.
F(x)
= 2x + 1, g(x)
=
![]()
f
![]() g(x)
= g(f(x))
=
g(x)
= g(f(x))
=![]() ,
,![]()
g![]() f(x)
= f(g(x))
= 2
f(x)
= f(g(x))
= 2![]() +1,
+1,![]() .
.
Из примера видно, что композиция некоммутативна:
f
![]() g(x)
≠ g
g(x)
≠ g![]() f(x),
зато ассоциативна: (f
f(x),
зато ассоциативна: (f
![]() g)
g)![]() h
= f
h
= f
![]() (g
(g![]() h).
h).
Предполагается, что области определения и значений функций f, g, h согласованы так, что композицию можно определить:
(f
![]() g)
g)![]() h(x)
= h(f
h(x)
= h(f
![]() g(x))
= h(g(f(x)))
g(x))
= h(g(f(x)))
f![]() (g
(g![]() h)(x)=
(g
h)(x)=
(g![]() h)(f(x))
= h(g(f(x)))
h)(f(x))
= h(g(f(x)))
Закон ассоциативности справедлив для любого числа функций, и та единственная функция, которая получается в результате композиции функций f1, f2, f3, … , fn в указанном порядке, так и обозначается:
f1
![]() f2
f2
![]() f3
f3
![]() …
…
![]() fn.
fn.
Пример.
F1 = x2, f2 = sin(x), f3 = x3 – 1
f1
![]() f2
f2
![]() f3
= (sin(x2))3
– 1,
f3
= (sin(x2))3
– 1,
f1
![]() f3
f3
![]() f2
= sin(x6
– 1),
f2
= sin(x6
– 1),
f2
![]() f1
f1
![]() f3
= sin6(x)
– 1,
f3
= sin6(x)
– 1,
f2
![]() f3
f3
![]() f1
= (sin3(x)-1)2,
f1
= (sin3(x)-1)2,
f3
![]() f1
f1
![]() f2
= sin(x3
– 1)2,
f2
= sin(x3
– 1)2,
f3
![]() f2
f2
![]() f1
= sin2(x3
– 1).
f1
= sin2(x3
– 1).
Пусть теперь функции f и g взаимнооднозначны. Если z = f(x), то
![]() –
взаимнооднозначная функция. Если y
= g(z),
то z = g-1(y)
– взаимнооднозначная функция. Выясним,
какими свойствами обладает композиция
взаимнооднозначных функций.
–
взаимнооднозначная функция. Если y
= g(z),
то z = g-1(y)
– взаимнооднозначная функция. Выясним,
какими свойствами обладает композиция
взаимнооднозначных функций.
Теорема.
Композиция взаимнооднозначных функций
– взаимнооднозначная функция, при этом
(f![]() g)-1
= g -1
g)-1
= g -1![]() f
-1.
f
-1.
Доказательство.
-
Пусть
 .
Тогда g(f(x1))
= g(f(x2))
= y. В силу взаимной
однозначности функции g:
f(x1)
= f(x2).
В силу взаимной однозначности функции
f: x1
= x2.
.
Тогда g(f(x1))
= g(f(x2))
= y. В силу взаимной
однозначности функции g:
f(x1)
= f(x2).
В силу взаимной однозначности функции
f: x1
= x2. -
Пусть
 .
.
Пусть g -1![]() f
-1(y)
=
f
-1(y)
=
![]() ,
тогда
,
тогда
![]()
Отсюда
![]() в силу условия взаимной однозначности
функций
в силу условия взаимной однозначности
функций
![]() и
и
![]() .
.
Таким образом, функции
![]() и
и
![]() отображают элемент y
в один и тот же элемент, т.е. представляют
собой одну и ту же функцию.
отображают элемент y
в один и тот же элемент, т.е. представляют
собой одну и ту же функцию.
Ядро функции).
Определяется обычным образом: Ker
f = f![]() f
-1
XX
(f: XY,
f -1:
YX).
f
-1
XX
(f: XY,
f -1:
YX).
Найдем сначала ядро взаимнооднозначной функции f:
f
![]() f
-1(x)
= f -1(f(x))
= f -1(y)
= x, f
-1
f
-1(x)
= f -1(f(x))
= f -1(y)
= x, f
-1![]() f(y)
= f(f
-1(y))
= f(x)
= y. Таким образом
ядро взаимнооднозначной функции –
тождественное отображение области
определения функции на нее же.
f(y)
= f(f
-1(y))
= f(x)
= y. Таким образом
ядро взаимнооднозначной функции –
тождественное отображение области
определения функции на нее же.
f
![]() f
-1
= Ix, f
-1
f
-1
= Ix, f
-1![]() f
= Iy.
f
= Iy.
В общем случае f -1 уже не функция, а просто бинарное отношение, и тогда справедлива следующая теорема.
Теорема.
Ядро функции является отношением эквивалентности на области определения функции.
Чтобы доказать эту теорему выясним какие упорядоченные пары принадлежат ядру функции f.
Пусть
![]() и
и
![]() и
и
![]() .
Если пара (x1,
x2) принадлежит
ядру, то у этой пары один и тот же образ.
Пусть f(x1)
= f(x2)
= y
(x1, y)f
и (x2,
y)f
(x1,
y)f
и (y, x2)f
-1
(x1,
x2)
f
.
Если пара (x1,
x2) принадлежит
ядру, то у этой пары один и тот же образ.
Пусть f(x1)
= f(x2)
= y
(x1, y)f
и (x2,
y)f
(x1,
y)f
и (y, x2)f
-1
(x1,
x2)
f
![]() f
-1.
f
-1.
Таким образом: (x1,
x2)
f
![]() f
-1
f(x1)
= f(x2).
f
-1
f(x1)
= f(x2).
Доказательство.
-
Рефлексивность: f(x) = f(x) (x, x)Ker f;
-
Симметричность: Если f(x1) = f(x2), то f(x2) = f(x1). Значит, ((x1, x2)Ker f (x2, x1) Ker f);
-
Транзитивность: Если f(x1) = f(x2), f(x2) = f(x3), то f(x1) = f(x3); (x1, x2)Ker f и (x2, x3) Ker f (x1, x3)Ker f.
Теорема доказана.
Всякое отношение эквивалентности определяет разбиение множества, на котором оно задано, на непересекающиеся непустые классы эквивалентности. В случае ядра функции, класс эквивалентности состоит из всех элементов области определения имеющих один и тот же образ.
Пример1.
Y = x2
(1, 1)Ker y, (1, -1)Ker y, (8, -8)Ker y, (0, 0)Ker y, (8, 2)Ker y.
Класс эквивалентности – это множество элементов [x] = {a| a2 = x2}
Например, [2]Ker y = {2; -2}, [0]Ker y = {0}.
Фактормножество области определения
X функции f
по ядру ker f
обозначим через
![]() .
Область значений функции f
обозначим через
.
Область значений функции f
обозначим через
![]() (от англ. Image
образ). Из сказанного следует, что
соответствие
(от англ. Image
образ). Из сказанного следует, что
соответствие
![]()
![]()
![]() по правилу
по правилу
![]()
это тотальная биекция.
это тотальная биекция.
Пример2 (теорема о гомоморфизме).
Определение. Группой
![]() называется произвольное множество, на
элементах которого определена функция
называется произвольное множество, на
элементах которого определена функция
![]() ,
которая называется «групповой
операцией» или «умножением»,
обозначается
,
которая называется «групповой
операцией» или «умножением»,
обозначается
![]() и обладает следующими свойствами.
и обладает следующими свойствами.
-
Ассоциативность.
 .
. -
Существование единицы.
 .
Элемент
.
Элемент
 называется единицей группы
называется единицей группы
 .
. -
Существование обратного элемента.
![]() .
Элемент
.
Элемент
![]() называется обратным элементу
называется обратным элементу
![]() .
.
Пусть
![]() две группы. Тотальная функция
две группы. Тотальная функция
![]() называется гомоморфизмом (от
гр. morphē
форма и гр. homos
равный, одинаковый; в сложных словах
означает сходство, единство), если она
сохраняет групповую операцию:
называется гомоморфизмом (от
гр. morphē
форма и гр. homos
равный, одинаковый; в сложных словах
означает сходство, единство), если она
сохраняет групповую операцию:
![]() .
Множество
.
Множество
Утверждение 1. Область значений
гомоморфизма
![]() множество
множество
![]() это
группа, подгруппа
это
группа, подгруппа
![]() ,
с той же самой групповой операцией.
,
с той же самой групповой операцией.
Доказательство.
Пусть
![]()
![]()
![]() .
Множество
.
Множество
![]() замкнуто относительно групповой
операции, заданной в группе
замкнуто относительно групповой
операции, заданной в группе
![]() ,
поэтому доказывать ассоциативность
операции не нужно.
,
поэтому доказывать ассоциативность
операции не нужно.
Покажем, что
![]() ,
где
,
где
![]() единица группы
единица группы
![]() ,
это единица множества
,
это единица множества
![]() .
Действительно,
.
Действительно,
![]() и
и
![]() .
.
Покажем, что
![]() это элемент, обратный элементу
это элемент, обратный элементу
![]() .
В самом деле:
.
В самом деле:
![]() и
и
![]()
=![]()
![]() .
Утверждение доказано.
.
Утверждение доказано.
Ядро гомомормизма
![]() ,
как ядро всякой функции, определяет
разбиение группы
,
как ядро всякой функции, определяет
разбиение группы
![]() ,
области определения функции
,
области определения функции
![]() ,
на непустые непересекающиеся классы
эквивалентности. Каждый класс
эквивалентности состоит из тех и только
тех аргументов, которые имеют один и
тот же образ.
,
на непустые непересекающиеся классы
эквивалентности. Каждый класс
эквивалентности состоит из тех и только
тех аргументов, которые имеют один и
тот же образ.
Утверждение 2. Множество классов
эквивалентности (фактормножество
![]() )
это группа, если
положить, что
)
это группа, если
положить, что
![]() для всяких
для всяких
![]() .
.
Доказательство. Пусть
![]() и
и
![]() .
Тогда
.
Тогда
![]()
![]() ,
поэтому групповая операция определена
корректно.
,
поэтому групповая операция определена
корректно.
Докажем ассоциативность групповой
операции:
![]()
![]() ,
так как умножение в группе
,
так как умножение в группе
![]() ассоциативно.
ассоциативно.
Докажем, что класс
![]() единица множества
единица множества
![]() .
.
![]() .
.
Докажем, что класс
![]() обратен классу
обратен классу
![]() .
.
![]() .
.
Утверждение доказано
Ранее было показано, что всякое
соответствие вида
![]() по правилу
по правилу
![]() является тотальной биекцией. Покажем,
что если
является тотальной биекцией. Покажем,
что если
![]() гомоморфизм, то
соответствие
гомоморфизм, то
соответствие
![]() тоже гомоморфизм.
тоже гомоморфизм.
![]() ,
что и требовалось.
,
что и требовалось.
Гомоморфизм, который одновременно есть
биекция, называется изоморфизмом
(от гр. isos
равный, одинаковый, подобный). Группы,
между которыми установлено изоморфное
соответствие, называются изоморфными.
Таким образом, нами доказана следующая
теорема об изоморфизме.
Факторгруппа
![]() по ядру произвольного гомоморфизма
по ядру произвольного гомоморфизма
![]() изоморфна группе образов этого
гомоморфизма.
изоморфна группе образов этого
гомоморфизма.
