2.7. Порядок определения ачх, фчх и афк
Передаточная функция системы, как известно, определяется как
Частотная передающая функция может
быть получена заменой p
на
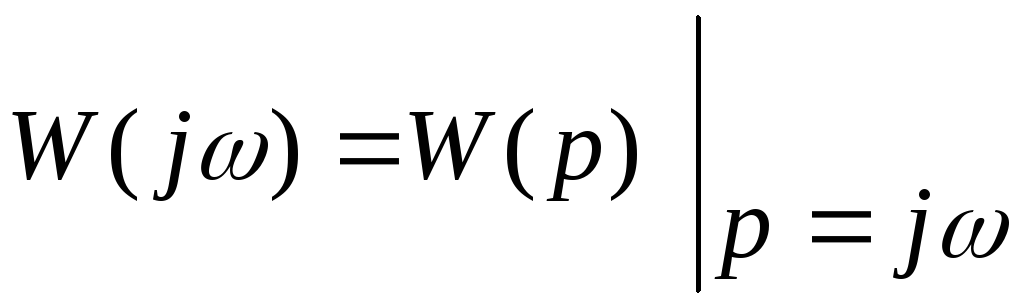
Как комплексное число ЧПФ может быть представлена
При этом
-
всегда четная
-
всегда нечетная, определяет знак
В общем виде ПФ может быть представлена в виде
Следовательно:
В общем виде
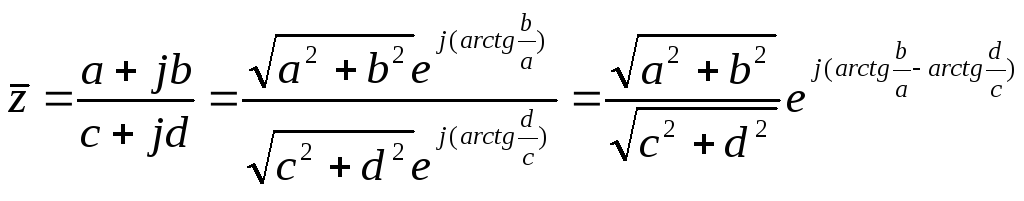
следовательно
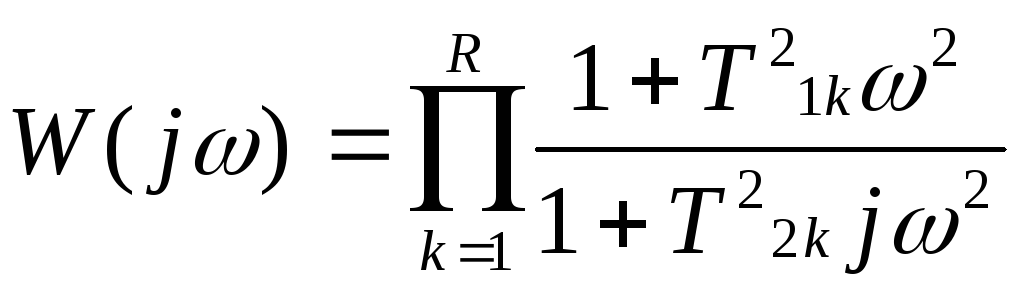
For example
следовательно
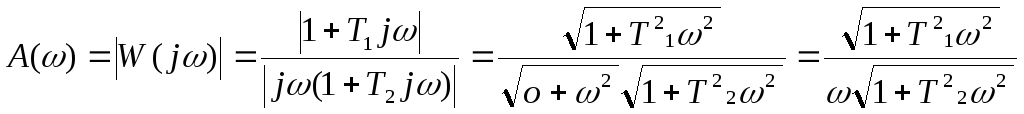
2.8. Логарифмическая амплитудная характеристика и ее построение
Метод построения ЛЧХ состоит в том, что АЧХ и ФЧХ исследуемой динамической системы изображают графически в виде непрерывных кривых, причем эти кривые строят в логарифмическом масштабе.
И называются они логарифмическая амплитудная частотная характеристика (ЛАХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ)
При этом ЛАХ строят приближенно в виде наскольких прямолинейных отрезков, называемых асимптотами ЛАХ, что существенно упрощает построение характеристики.
Такие ЛАХ называются асимптотическими
Как известно, между АЧХ и ФЧХ существует однозначная связь, следовательно можно ограничиться только построением ЛАХ, так как в ней содержится вся информация о САУ.
Если в САУ такая связь существует, такая система называется минимально-фазаовой, мы рассматриваем именно такие звенья.
То есть: корни характеристических уравнений, соответствующих числителю и знаменателю, имеют отрицательные вещественные части.
Пусть имеется некая ЧПФ
ЛАХ определен как
Частота откладывается по оси абсцисс
в логарифмическом масштабе, а по оси
ординат – значение функции
.
Построение асимптотической ЛАХ рассмотрим на примерах.
1.
Пусть
Принято, что постоянные времени нумеруются по убыванию их честленных значений, то есть
Алгоритм нахождения характеристик
Пусть известны ПФ и
замкнутой,
или
разомкнутой
системы
Делаем подстановку
Получаем частотную ПФ
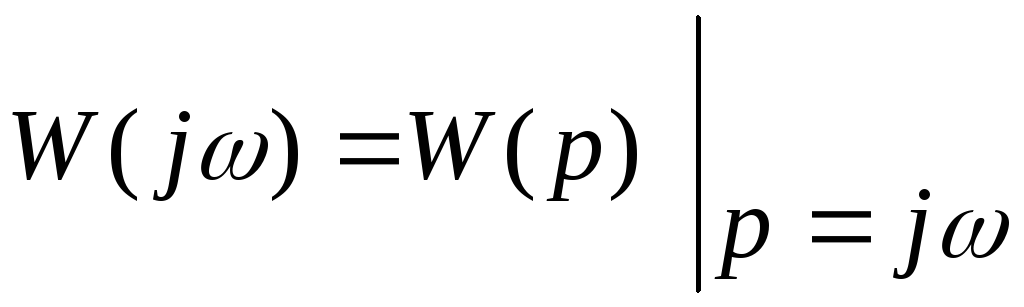
Как известно,
АЧХ:
ФЧХ:
В ЛАХ
Запишем ЧПФ
Выразим
,
,
через частоты
,
,
,
причем
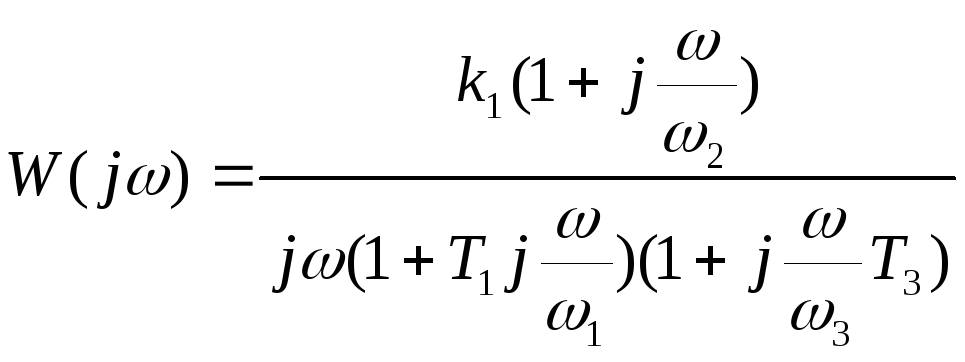
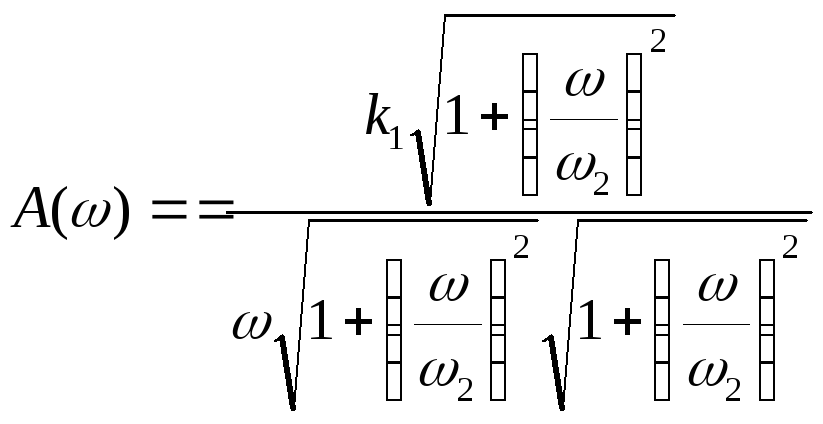
Рассмотрим 4 участка этой характеристики
1.
2.
3.
4.
При построении асимптотических ЛАХ
принято, что выражение
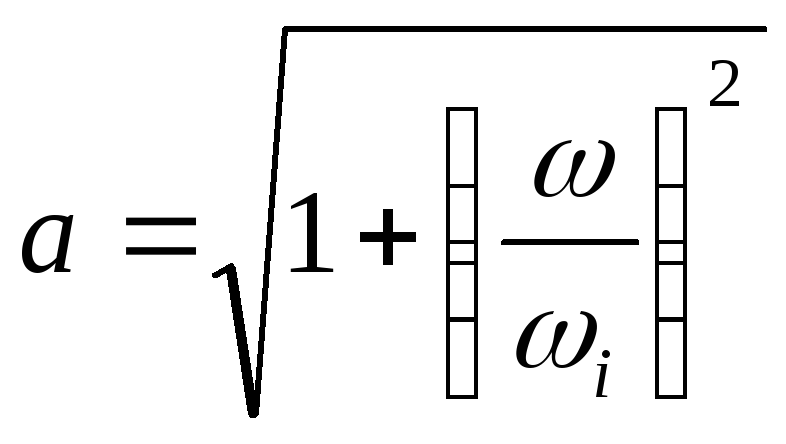может
принимать только два значения
Если
,
то
Если
,
то
Определим ЛАХ:
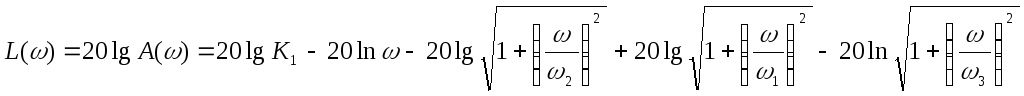
логарифмируются сначала коэффициенты, потом частота, \потом все остальные сомножители в порядке возрастания частот.
Ось абсцисс – частота в логарифмическом масштабы, размерность рад/с или декада
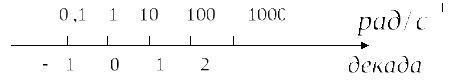
Увеличение частоты в 10 раз, т.е. на одну
декаду, влечет изменение
на 20 децибел.
Существует такое понятие как эталонный
наклон, равный -20дБ/дек, что соответствует
в ПФ.
Рассматриваем участки
1.
При частоте 1рад/с
2.
3.
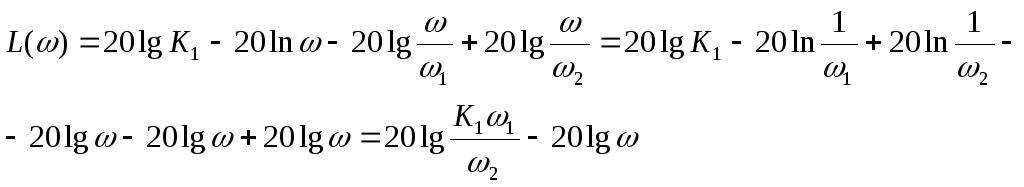
4.
