2.5. Временные характеристики сау

Временная характеристика – это отклик САУ на некоторое типовое входное воздействие.

При известной ПФ системы или и заданном входным воздействием временные характеристики можно определять по стандартным таблицам преобразований Лапласа.

То есть, зная изображения входного воздействия и ПФ, можно получить изображение управляемой величины и затем – сам сигнал

Для получения временных характеристик используются, в основном, 2 типовых входных воздействия: и единичный скачок.

Весовая функция - это отклик САУ на входной сигнал в виде , то есть, если входное воздействие , что на выходе системы имеем

Что такое ?

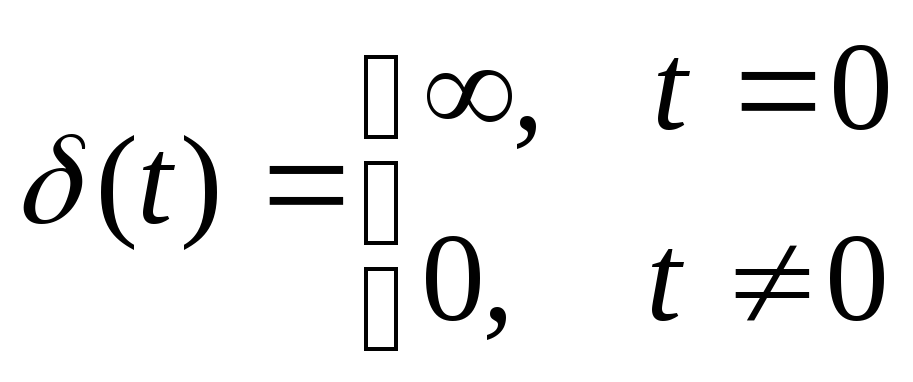
Причем

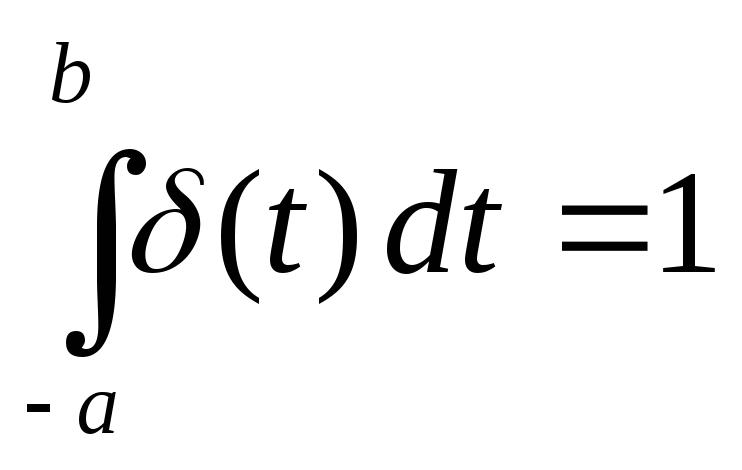, для любых a и b > 0

обладает фильтрующим свойством. Для любой ограниченной функции f(t):

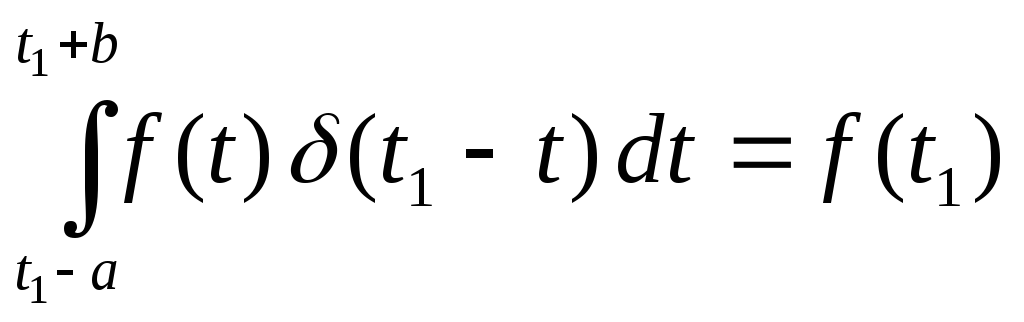
Найдем изображение по Лапласу входной величины

, по таблице

По рассмотренному уже нами алгоритму можно определить отклик звена, т.е. весовую функцию

Т.о. весовая функция и ПФ связаны между собой преобразованием Лапласа.

При известной весовой функцииотклик системы на произвольное входное воздействие может быть найдена с помощью интеграла Дирихле

Для определения показателей качества САУ обычно используется переходная характеристика – отклик системы на единичный скачок

Что такое единичный скачок?

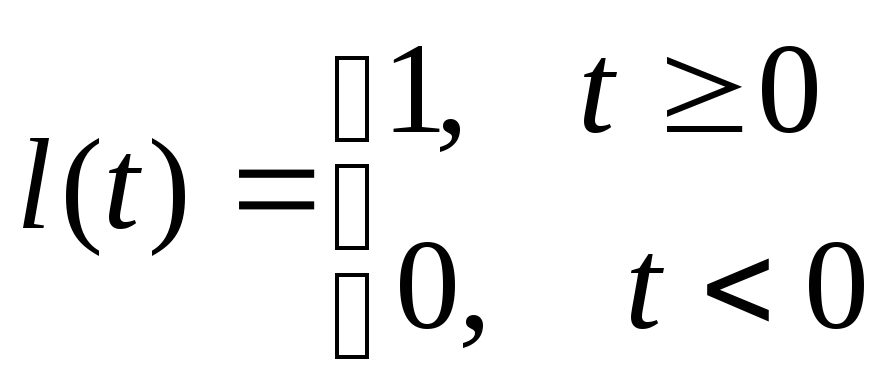
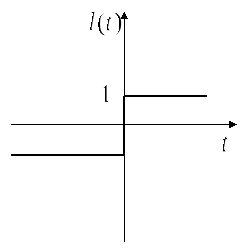
Его изображение по Лапласу:

Отклик САУ на единичный скачок – переходная характеристика системы определяется

По виду переходной характеристики судят об устойчивости системы.

2.6. Частотные характеристики сау

Частотные методы исследования АС основаны на рассмотрении установившейся реакции системы на гармоническое входное воздействие

Используется в задачах анализа АС

(Для задач анализа удобнее использовать метод ЛЧХ)

Рассмотрим, как обычно, САУ, котроая описывается дифференциальным уравнением

Нас интересует установившаяся реакция этой системы на входное гармоническое воздействие.

Его мы представим в комплексном виде

Здесь:

- амплитуда гармонических колебаний

- круговая частота колебаний

-начальная фаза

- комплексная амплитуда колебаний

На выходе линейной САУ будет отклик:

Описание и подставляем в дифференциальное уравнение

Но учтем при этом, что

Подставляем в дифференциальное уравнение, получаем

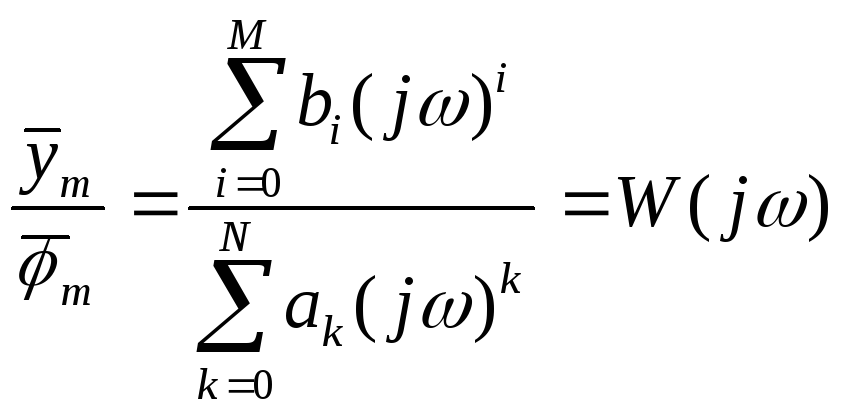
- частотная ПФ системы, описываемой (2.2)

Как видим, формально ЧПФ может быть получена из ПФ, рассмотренной в 2.1, заменой Лапласа на

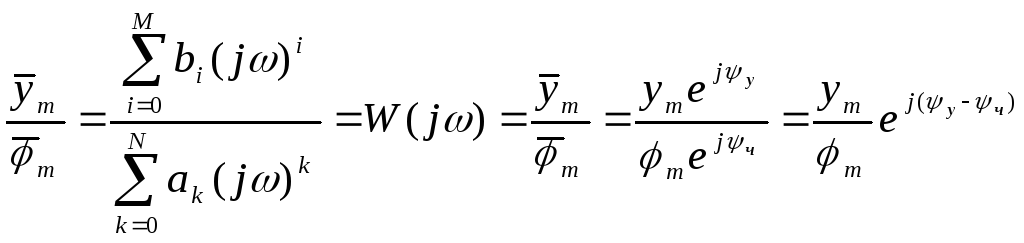
- АЧХ

- ФЧХ

АЧХ:

Отношение амплитуд гармонических колебаний на выходе и входе системы как функция частоты этих колебаний.

ФЧХ:

Разность фар между выходной и входной величинами как функция частоты этих колебаний.

Как и всякая комплексная величина, ЧПФ может быть представлена:

или

При этом

Частотная ПФ графически на комплексной плоскости в виде вектора с координатами или с полярными

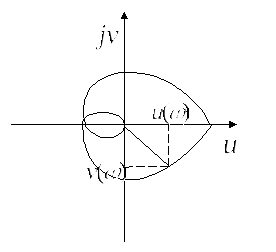
При изменении в пределах , конец вектора описывает кривую, которая называется амплитудно-фазовой характеристикой С АПХ

ЧПФ – полностью описывает прохождение гармонического сигнала через динамическую систему

Если мы имеем произвольное негармоническое входное воздействие, ЧПФ системы равна отношению изображений по Фурье выходного и входного сигналов.