
- •"Комп’ютерні методи дослідження інформаційних процесів та систем"
- •6.170103 "Управління інформаційною безпекою" Затверджено
- •Чисельне інтегрування функцій однієї змінної
- •Похибка методу прямокутників
- •Похибка методу
- •Метод Сімпсона
- •Метод Гаусса
- •Метод Чебишoва
- •2.Завдання до лабораторної роботи
- •2.1. Домашня підготовка до роботи
- •2.2. Робота в лабораторії
- •Контрольні запитання
- •Список літератури
- •"Комп’ютерні методи дослідження інформаційних процесів та систем"
- •6.170103 "Управління інформаційною безпекою"
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ "ЛЬВІВСЬКА ПОЛІТЕХНІКА"
ЧИСЛОВЕ ІНТЕГРУВАННЯ
ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ
Методичні вказівки
до лабораторної роботи № 4
з курсу
"Комп’ютерні методи дослідження інформаційних процесів та систем"
для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації",
6.170103 "Управління інформаційною безпекою" Затверджено
на засіданні кафедри
«Безпека інформаційних
технологій»
Протокол № 12 від 12.05.2011р.
Львів – 2011
Чисельне інтегрування функцій однієї змінної: Методичні вказівки до лабораторної роботи №4 з курсу "Комп’ютерні методи дослідження інформаційних процесів та систем" для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації", 6.170103 "Управління інформаційною безпекою" /Укл.: Л.В. Мороз, А.Я. Горпенюк, Н.М. Лужецька - Львів: Видавництво НУ“ЛП”, 2011.- 14 с.
Укладачі: Л.В. Мороз, к.т.н., доц.
А.Я. Горпенюк, к.т.н., доц.
Н.М. Лужецька, асист.
Відповідальний за випуск: В.М. Максимович, д.т.н., проф.
Рецензент: В.В. Хома, д.т.н., проф.
А.Е. Лагун, к.т.н., доц.,
Мета роботи – ознайомлення з методами наближеного обчислення означених інтегралів.
Чисельне інтегрування функцій однієї змінної
Нехай
задана деяка функція
![]() на відрізку
на відрізку
![]() .
Розглянемо задачу обчислення її
означеного інтеграла
.
Розглянемо задачу обчислення її
означеного інтеграла
![]() .
.
Якщо
для
![]() відома первісна
відома первісна
![]() ,
то інтеграл обчислюється за формулою
Ньютона - Лейбніца
,
то інтеграл обчислюється за формулою
Ньютона - Лейбніца
![]() (1)
(1)
Однак
для великого класу функцій
![]() не можна виразити через елементарні
функції, тому означений інтеграл не
можна обчислити за допомогою формули
Ньютона - Лейбніца. Бувають також випадки,
коли підінтегральна функція задається
таблично. Тоді використовують формули
наближеного інтегрування, які називають
квадратурними. Сам процес чисельного
визначення інтегралу називають
квадратурою.
не можна виразити через елементарні
функції, тому означений інтеграл не
можна обчислити за допомогою формули
Ньютона - Лейбніца. Бувають також випадки,
коли підінтегральна функція задається
таблично. Тоді використовують формули
наближеного інтегрування, які називають
квадратурними. Сам процес чисельного
визначення інтегралу називають
квадратурою.
Ідея чисельних методів інтегрування в наступному. означений інтеграл

![]()
можна
трактувати як площу фігури (Рис.1),
обмеженої ординатами a
і b
, віссю абсцис
![]() і графіком підінтегральної функції
і графіком підінтегральної функції
![]() (криволінійною трапецією).
(криволінійною трапецією).
Рис.
1
Рис.
2

![]() ,
площа якої обчислюється значно простіше.
,
площа якої обчислюється значно простіше.
Найбільш прості формули чисельного інтегрування - формули прямокутників та трапецій.
Розглянемо метод прямокутників.
Відрізок
![]() розбивають на
розбивають на
![]() відрізків
відрізків
![]() ,
де i=
,
де i=![]() . На кожному з відрізків
. На кожному з відрізків
![]() площа криволінійної трапеції заміняється
площею прямокутника з основою
площа криволінійної трапеції заміняється
площею прямокутника з основою
![]() та висотою
та висотою
![]() .
.
Тоді
 (2)
(2)
Якщо
відрізки
![]() рівновеликі :
рівновеликі :
![]()
 (3)
(3)
Формулу
(3) називають також формулою «середніх»
прямокутників. Якщо за висоту прямокутника
взяти
![]() або
або
![]() ,
то можна одержати формули «лівих» та,
відповідно, «правих» прямокутників.
,
то можна одержати формули «лівих» та,
відповідно, «правих» прямокутників.
Формула лівих прямокутників :
![]() .
.
Формула правих прямокутників :
![]() .
.
Похибка методу прямокутників
( гранична абсолютна похибка, похибка квадратурної формули (3) ):
![]() (4)
(4)
де
![]() , x[a;b]
.
, x[a;b]
.
Вираз (4) для похибки показує, що формула (3) є точною для будь-якої лінійної функції, оскільки друга похідна такої функції дорівнює нулю, а отже похибка теж дорівнює нулю.
Рис.
3
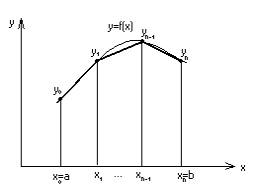
Розіб’ємо
відрізок інтегрування
![]() на n
рівних частин, довжиною
на n
рівних частин, довжиною
![]() .
.
На
кожній такій частині дуга кривої
![]() заміняється стягуючою її хордою. В
точках розбиття проведемо ординати до
перетину з кривою
заміняється стягуючою її хордою. В
точках розбиття проведемо ординати до
перетину з кривою
![]() .
Кінці ординат з’єднаємо прямолінійними
відрізками. Тоді можна замінити кожну
з одержаних криволінійних трапецій
прямолінійною (Рис.3). Площа криволінійної
трапеції
.
Кінці ординат з’єднаємо прямолінійними
відрізками. Тоді можна замінити кожну
з одержаних криволінійних трапецій
прямолінійною (Рис.3). Площа криволінійної
трапеції
![]() наближено дорівнює сумі площ прямолінійних
трапецій.
наближено дорівнює сумі площ прямолінійних
трапецій.
Площа лівої трапеції
![]()
Відповідно
для трапеції, розміщеної над ділянкою
![]() знайдемо:
знайдемо:
![]() (5)
(5)
Звідси
![]()
 (6)
(6)
Або
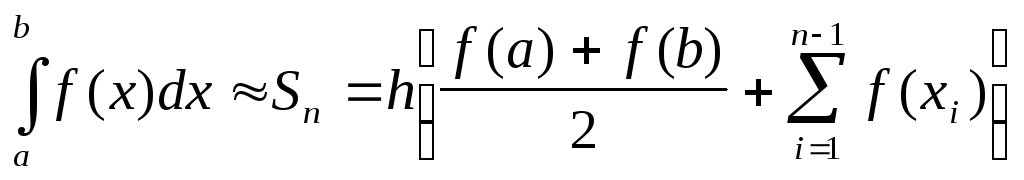 (7)
(7)
