МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ "ЛЬВІВСЬКА ПОЛІТЕХНІКА"
ІТЕРАЦІЙНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ СИСТЕМ
ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
Методичні вказівки
до лабораторної роботи № 3
з курсу
"Комп’ютерні методи дослідження інформаційних процесів та систем"
для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації",
6.170103 "Управління інформаційною безпекою" Затверджено
на засіданні кафедри
«Безпека інформаційних
технологій»
Протокол № 12 від 12.05.2011р.
Львів – 2011
Ітераційні методи розв’язування систем лінійних алгебраїчних рівнянь: Методичні вказівки до лабораторної роботи №3 з курсу "Комп’ютерні методи дослідження інформаційних процесів та систем" для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації", 6.170103 "Управління інформаційною безпекою" / Укл.: Л.В. Мороз, А.Я. Горпенюк, Н.М. Лужецька - Львів: Видавництво НУ“ЛП”, 2011..- 12 с.
Укладачі: Л.В. Мороз, к.т.н., доц.
А.Я. Горпенюк, к.т.н., доц.
Н.М. Лужецька, асист.
Відповідальний за випуск: В.М. Максимович, д.т.н., проф.
Рецензент: В.В. Хома, д.т.н., проф.
А.Е. Лагун, к.т.н., доц.,
Мета роботи – ознайомлення з ітераційними методами розв’язування систем лінійних алгебраїчних рівнянь.
Ітераційні методи розв’язування систем лінійних
алгебраїчних
рівнянь
До ітераційних методів належать: метод простої ітерації, метод Зейделя, метод верхньої релаксації та інші.
Метод простої ітерації.
Нехай задано лінійну систему
(1)
Розглянемо матриці
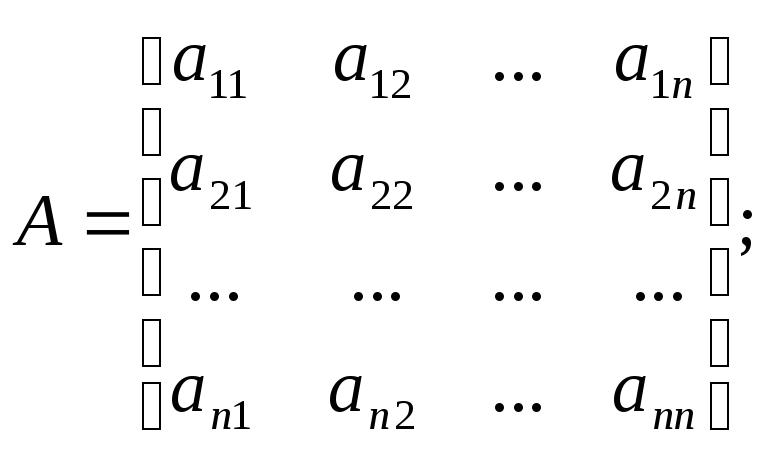
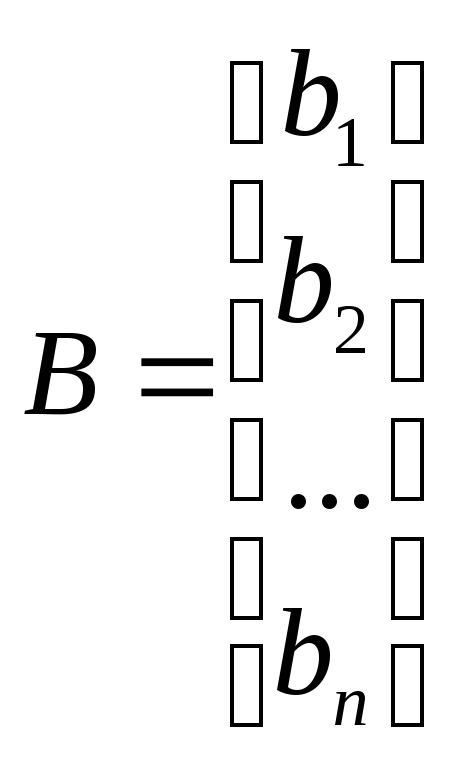
Тоді систему (1) можна записати у вигляді матричного рівняння
(2)
Будемо
вважати, що діагональні коефіцієнти
(і
=
1, 2,…, n).
Розв’яжемо
перше рівняння системи (1) відносно
,
друге відносно
і т.д. Тоді одержимо еквівалентну систему
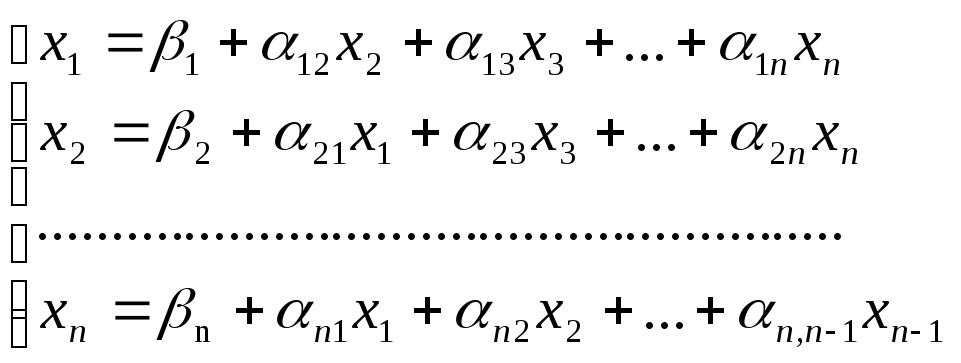(3)
де
,
при
;
,
при
;
;
;
Кажуть, що система (3) зведена до нормального вигляду.
Введемо матриці та
Систему (3) запишемо у вигляді
(4)
Систему
(3) будемо розв’язувати методом послідовних
наближень. За нульове наближення
позначимо, наприклад, стовпчик вільних
членів
.
Далі послідовно будуємо матриці-стовпці
наступних наближень розв’язку
системи (4):
– перше
наближення
– друге
наближення і т.д.
Будь-яке (k + 1)-е наближення обчислюється за формулою:
,
(k
= 0,
1, 2, …) (5)
В
розгорнутому вигляді
.
Якщо
послідовність наближень
має границю
, (6)
то ця границя є розв’язком системи (3).
На
практиці ітераційний процес припиняють,
коли
,
де
– гранична абсолютна похибка.
Приклад. Розв’язати систему методом простої ітерації:
.
Зведемо систему до нормального вигляду
(7)
або в матричній формі
(8)
За нульові наближення коренів системи приймаємо вектор вільних членів:
.
Підставляємо ці значення в праві частини системи (7). Одержимо перші наближення коренів
Далі знаходимо другі і треті наближення коренів
Умови збіжності ітераційного процесу Нехай задано зведена до нормального вигляду система лінійних рівнянь
Умова збіжності: якщо сума модулів елементів рядків або модулів елементів стовпців матриці α менша ніж 1, то процес ітерації для даної системи збігається до єдиного розв’язку незалежно від вибору вектора початкових наближень.