
3 Плоскость
В отличие от точки и прямой плоскость на чертеже задается не проекциями, а родственным соответствием (т.е. тремя парами соответственных точек, как показано на рисунке 3).
Наиболее распространенные способы задания такого соответствия - это симплекс (три точки, объединенные в треугольник) и следы (линии пересечения плоскости с плоскостями проекции). Возможны и другие вариации трех точек (параллельные и пересекающиеся прямые и т.п.).

Рисунок 3 - Задание плоскости на эпюре
Условие принадлежности прямой плоскости вытекает из способа ее задания на чертеже. Если две точки прямой принадлежат плоскости, то и вся прямая ей принадлежит.

Рисунок 4 - Главные линии плоскости
Принадлежность точки плоскости сводится к определению принадлежности точки одной из прямых этой плоскости.
Прямые, лежащие в плоскости и параллельные плоскостям проекции (h - горизонталь, f - фронталь на рисунке 4) получили названия линий уровня плоскости (следы - линии нулевого уровня). Линии же, перпендикулярные им, называют линиями наибольшего наклона (ската).
Обобщающее название линий уровня и наибольшего ската - главные линии плоскости.
Пример решения задачи. Определить принадлежит ли точка М плоскости треугольника АВС.
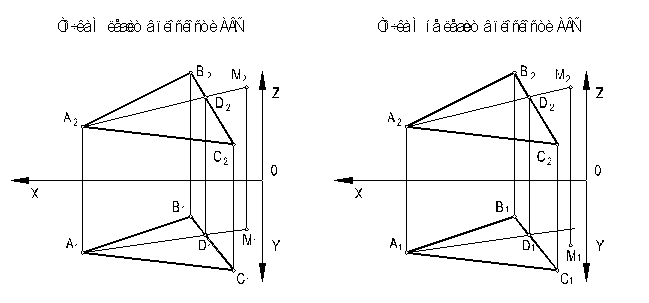
Рисунок 5 - Принадлежность точки плоскости
Точка М может быть отнесена к одной из линий плоскости треугольника АВС (например, к прямой АМ ). Это и определяет стратегию решения.
1) Проводится (для определенности) через точку М2 фронтальная проекция прямой А2D2.
Тогда из условия принадлежности этой прямой плоскости, она должна проходить через точку D плоскости АВС, и можно построить ее горизонтальную проекцию.
2) По соответствию, находится горизонтальная проекция точки D ( D1 на горизонтальной проекции прямой B1 C1 ).
3) Строится горизонтальная проекция прямой A1D1.
Анализ чертежа показывает, принадлежит точка M прямой AD или нет (проекции точек должны принадлежать соответствующим проекциям прямым). Это позволяет сделать вывод о том, что и сама точка в рассматриваемой плоскости лежит или не лежит, как показано на рисунке 5.
Решить на комплексном чертеже самостоятельно следующие задачи по теме "Плоскость".
3.1 Построить точку M , лежащую в плоскости треугольникам ABC . Горизонтальная проекция точки M определяется координатами (70,30), [A(10,10,10), B(30,60,40), С(60,20,30)].
3.2 Через точку G(40,30,10) провести плоскость общего положения Q . Плоскость задать следами.
3.3 Как расположена точка G (задача 3.2) по отношению к плоскости треугольника АВС (задача 3.1).
3.4 Прямая LT лежит в плоскости Q (плоскость общего положения задать следами). Построить ее горизонтальную проекцию если известно, что фронтальная определяется точками L2 (30,20) и T2 (60,40).
3.5 Через точку М(50,50,50) провести прямую параллельную плоскости общего положения, проходящую через прямую АВ. Плоскость задать следами.[A(10,10,40), B(40,30,20)].
Пример решения задачи
Две плоскости P и Q в трехмерном пространстве пересекаются по прямой линии 1. Рассмотрим задачу на ее построение.

Рисунок 6 - Пересечение плоскостей
Пусть обе плоскости P и Q заданы следами (рисунок 6).
1) Фронтальные следы плоскостей P2 и Q2 лежат в одной плоскости проекции π2 и следовательно пересекаются в точке M .
2) Аналогично дело обстоит и с горизонтальными следами P1 и Q1 : они пересекаются в горизонтальной плоскости π1 в точке N.
Эти две точки M и N одновременно принадлежат обеим плоскостям P и Q и, следовательно, определяют линию одновременно принадлежащую двум плоскостям, или, другими словами, линию пересечения.
В случае, когда пересекающие плоскости заданы менее удобным образом (рисунок 7), например одна ( Q ) следами, а другая симплексом (треугольником ABC),задача может быть сведена к уже рассмотренной: в первом варианте находятся следы плоскости заданной треугольником, и тогда задача сводится к рассмотренной выше; во втором используется известное утверждение о том, что три плоскости всегда пересекаются в одной точке. Остановимся на втором варианте.

Рисунок 7 - Пересечение плоскостей
Введение горизонтальной плоскости уровня Q' приведет к тому, что исходные плоскости пересекутся с ней по горизонталям h' и 1С, которые пересекутся по точке N (эта точка одновременно принадлежит трем плоскостям Q ', P и ABC ) и, следовательно, эту точку можно отнести к линии пересечения.
Повторное введение плоскости уровня Q" позволит получить еще одну точку линии пересечения M .
Решить на комплексном чертеже самостоятельно следующие задачи по теме "Плоскость".
3.6 Построить линию пересечения плоскостей общего положения P и Q , заданных следами. Следы взять произвольно, считая, что точка D(70,30,10) лежит в плоскости P , а точка B(10,10,20) в плоскости Q
3.7 Построить линию пересечения плоскости P (задача 3.6) с плоскостью треугольника АВС (задача 3.1).
3.8 Построить точку пересечения линии общего положения DB (задача 3.6) с плоскостью общего положения P, заданной следами и проходящей через точкуS(40,40,40).
3.9 Найти точку пересечения прямой общего положения АE с плоскостью пересекающихся прямых (задача 2.5), А(35,20,30), Е(20,35,5).
3.10 Найти точку пересечения горизонтально- проецирующей прямой, проходящей через точку E(50,20,20), с плоскостью Q (задача 3.6).
Пример решения задачи. Задачи на построение точки пересечения прямой и плоскости решаются сведением их к задачам на пересечение плоскостей. Рассмотрим один из возможных вариантов.
Пусть требуется найти точку пересечения прямой t, заданной отрезком АВ, и плоскости общего положения Q , заданной следами (рисунок 8).
Прямая t может быть отнесена к одной из проецирующих плоскостей, для определенности будем считать, что к фронтально -проецирующей плоскости P . Тогда плоскости P и Q пересекутся по линии MN и в силу того, что линии t и MN лежат в одной плоскости P, они пересекутся в точке S . Эта точка одновременно принадлежит прямой и плоскости и, следовательно, является искомой точкой пересечения.

Рисунок 8 - Точка встречи прямой с плоскостью
