11 Вопрос Графические характеристики случайных величин. Гистограмма. Характеристики положения (мода, медиана, выборочная средняя)

Дли повышения наглядности эмпирических распределений, используется их графическое представление. Наиболее распространенными способами графического представления являются гистограмма, полигон частот и полигон накопленных частот (кумулята).

Полигон частот – графическое изображение дискретного статистического ряда распределения.

Пусть необходимо изучить распределение значений признака Х у объектов некоторой генеральной совокупности. С этой целью из данной генеральной совокупности извлекают некоторую выборочную совокупность объёмом n. Пусть в полученной выборке х₁ признака встречается m₁ раз, следующее по величине значение x₂-m₂ и т.д. Если результаты представить в виде таблицы, в первой строке которой в порядке возрастания перечислены все варианты х_i, а во второй соответствующие им частоты, то получим таблицу:

X	X1	X2	….	xr
m	M1	M2	…	mr

Такую таблицу называют статистическим дискретным рядом распределения. Для графического изображения подобного ряда на координатной плоскости откладывают точки и соединяют их отрезками прямых.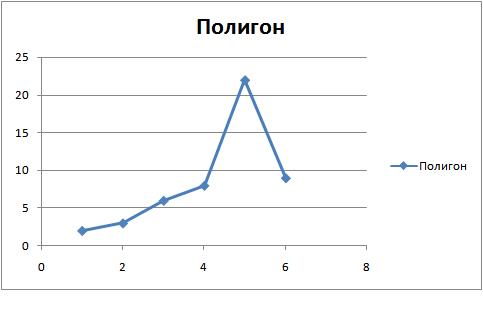

Гистограмма частот – фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной х, а высотами – отношения m₁: х (плотности частот). Используется при большом количестве вариантов, результаты записывают в виде статистического интервального ряда распределения. Гистограмма частот – графическое изображение интервального ряда распределения.

Нередко на практике во второй строке таблицы указывают не частоты m_i а относительные частоты P_i=m_{i /} n, сумма которых равна единице. Графическим изображением такого ряда распределения является гистограмма относительных частот, которая соответствует гистограмме частот.

Кумулята служит для графического изображения кумулятивного вариационного ряда. Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат - накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты - соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой.

Количество баллов 1 2 3 4 5 6 7 8 9 10 11 12

Частота 1 1 2 3 4 4 6 5 3 3 2 1

Накопленная частота n 1 2 4 7 11 15 21 26 29 32 34 35

Числовой характеристикой выборки, как правило, не требующей вычислений, является так называемая мода. Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке. Для симметричных распределений признаков, в том числе для нормального распределения, значение моды совпадает со значениями среднего и медианы. Для других типов распределении, несимметричных, это не характерно. К примеру, в последовательности значений признаков 1, 2, 5, 2, 4, 2, 6, 7, 2 модой является значение 2, так как оно встречается чаще других значений - четыре раза.

Медианой называется значение изучаемого признака, которое делит выборку, упорядоченную по величине данного признака, пополам. Справа и слева от медианы в упорядоченном ряду остается по одинаковому количеству признаков. Например, для выборки 2, 3, 4, 4, 5, 6, 8, 7, 9 медианой будет значение 5, так как слева и справа от него остается по четыре показателя. Если ряд включает в себя четное число признаков, то медианой будет среднее, взятое как полусумма величин двух центральных значений ряда. Для следующего ряда 0, 1, 1, 2, 3, 4, 5, 5, 6, 7 медиана будет равна 3,5.

Выборочное среднее (среднее арифметическое) значение как статистический показатель представляет собой среднюю оценку изучаемого в эксперименте психологического качества. Эта оценка характеризует степень его развития в целом у той группы испытуемых, которая была подвергнута психодиагностическому обследованию. Сравнивая непосредственно средние значения двух или нескольких выборок, мы можем судить об относительной степени развития у людей, составляющих эти выборки, оцениваемого качества.

Выборочное среднее определяется при помощи следующей формулы:

где х - выборочная средняя величина или среднее арифметическое значение по выборке; n - количество испытуемых в выборке или частных психодиагностических показателей, на основе которых вычисляется средняя величина; хk - частные значения показателей у отдельных испытуемых.