4.3. Моделирование сезонных колебаний

Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели следующий:

. (4.3)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (), сезонной () и случайной () компонент.

Общий вид мультипликативной модели выглядит так:

. (4.4)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (), сезонной () и случайной () компонент.

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений , и для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1. Выравнивание исходного ряда методом скользящей средней.

2. Расчет значений сезонной компоненты .

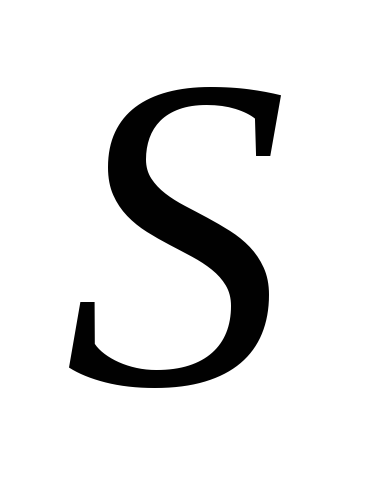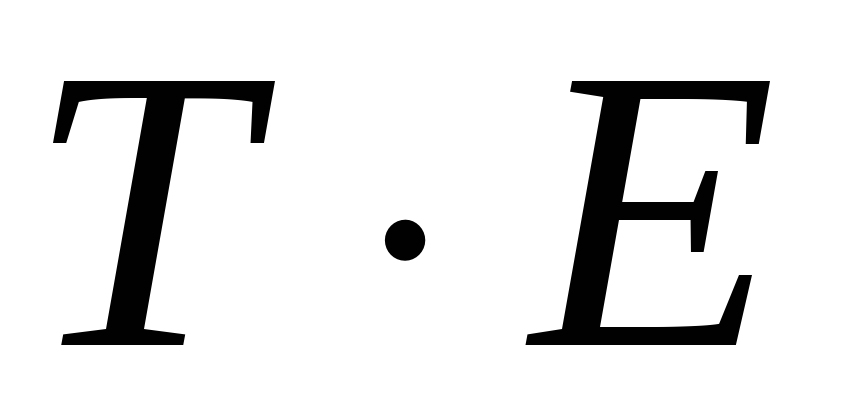3. Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных () в аддитивной или () в мультипликативной модели.

4. Аналитическое выравнивание уровне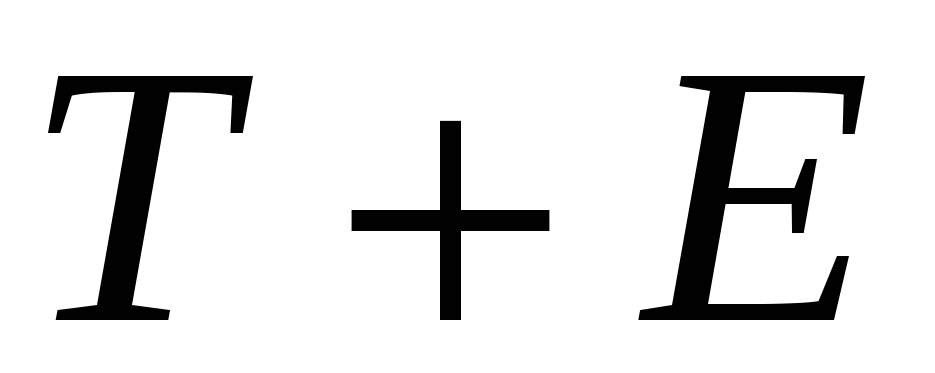й () или (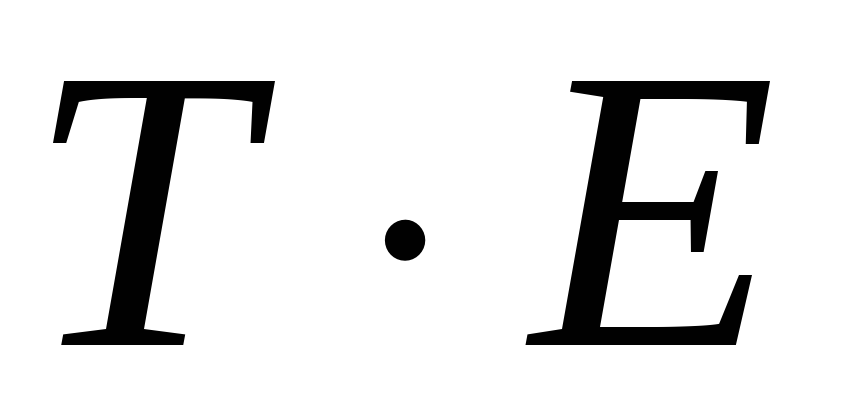) и расчет значений 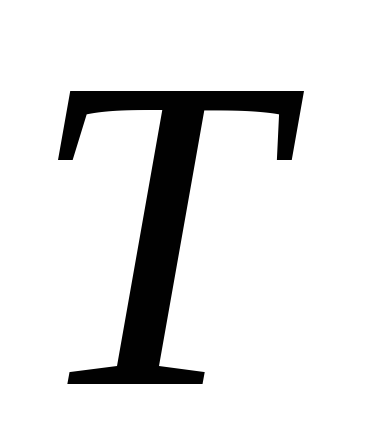с использованием полученного уравнения тренда.

5. Расчет полученных по модели значений (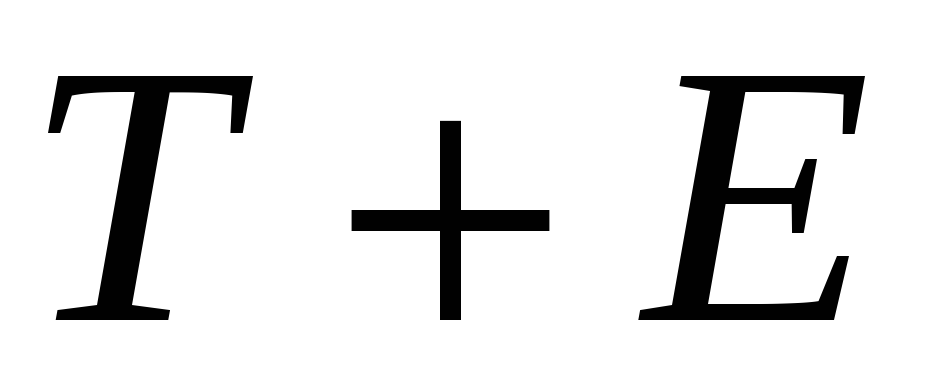) или ().

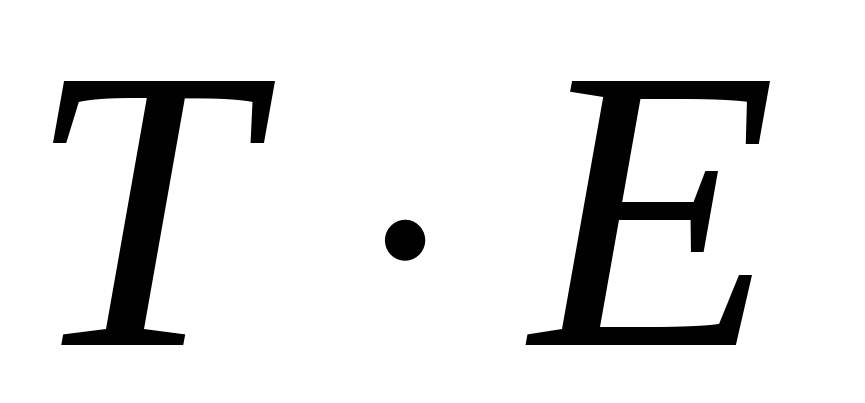6. Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.

В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле.

Скорректированные значения сезонной компоненты в аддитивной модели равны , где 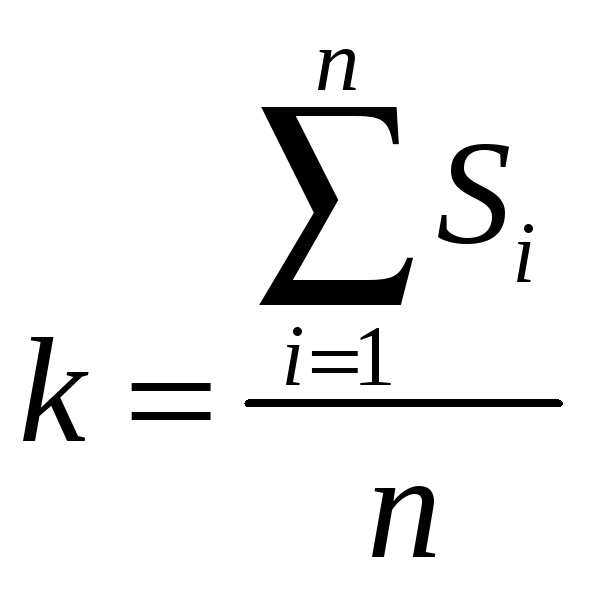, в мультипликативной модели получаются при умножении ее средней оценки на корректирующий коэффициент , где .

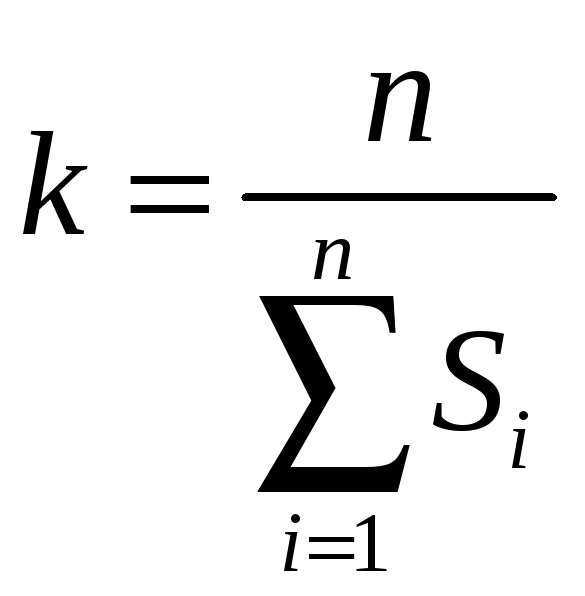Прогнозное значение уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент, в мультипликативной модели есть произведение трендовой и сезонной компонент.

4.4. Автокорреляция в остатках. Критерий Дарбина-Уотсона

Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.

1. Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.

2. В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени .

Один из более распространенных методов определения автокорреляции в остатках – это расчет критерия Дарбина-Уотсона:

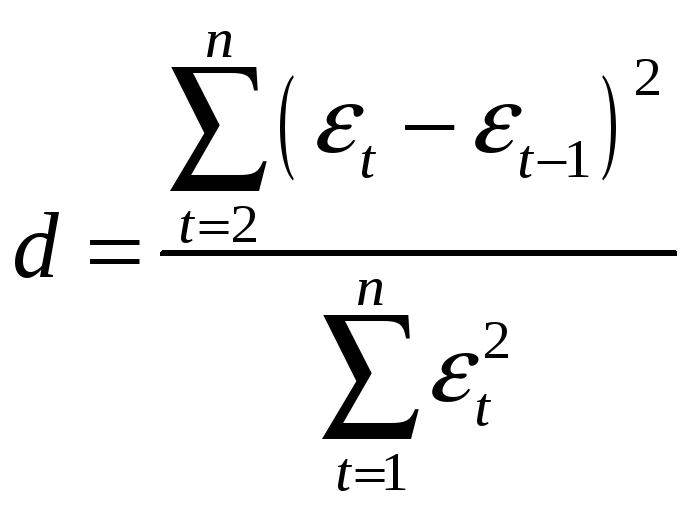. (4.5)

Т.е. величина есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.

Можно показать, что при больших значениях существует следующее соотношение между критерием Дарбина-Уотсона и коэффициентом автокорреляции остатков первого порядка : .

Таким образом, если в остатках существует полная положительная автокорреляция и , то . Если в остатках полная отрицательная автокорреляция, то и, следовательно, . Если автокорреляция остатков отсутствует, то и . Т.е. .

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотезы и состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона и для заданного числа наблюдений , числа независимых переменных модели и уровня значимости . По этим значениям числовой промежуток разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью осуществляется следующим образом:

– есть положительная автокорреляция остатков, отклоняется, с вероятностью принимается ;

– зона неопределенности;

– нет оснований отклонять , т.е. автокорреляция остатков отсутствует;

– зона неопределенности;

– есть отрицательная автокорреляция остатков, отклоняется, с вероятностью принимается .

Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу .