1.6. Система сходящихся сил

Система сил называется сходящейся, если линии действия всех сил, составляющих систему, пересекаются в одной точке. Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна сумме этих сил и проходит через точку пересечения их линий действия (рис.1.24).

(1.9)

Равнодействующая может быть определена последовательным применением правила параллелограмма ко всем силам системы. Построение может быть упрощено, если вместо параллелограммов построить силовой многоугольник (рис. 1.24).

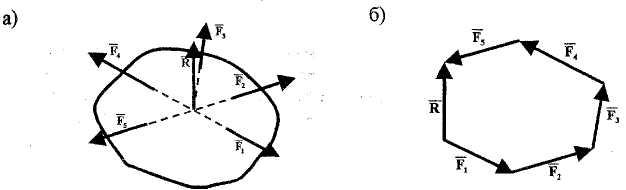
Рис. 1.24

В этом случае все силы системы соединяются последовательно. Начало вектора равнодействующей будет совпадать с началом первого суммируемого вектора, а конец - с концом последнего из суммируемых векторов. Частным случаем многоугольника сил является треугольник сил, который можно рассматривать как половину параллелограмма сил (рис. 1.25,а,б).

Рис. 1.25

Если многоугольник сил строится в определенном масштабе, то модуль и направление равнодействующей могут быть определены непосредственно из чертежа. Если без масштаба, то для определения модуля и направления равнодействующей можно использовать известные тригонометрические зависимости. Так, для треугольника сил модуль равнодействующей может быть определен с использованием формулы, вытекающей из теоремы косинусов:

,

где а - угол между векторами и .

Если угол между двумя суммируемыми векторами (,) прямой, то для определения модуля равнодействующей () можно использовать теорему Пифагора:

(1.10)

Если суммируются три взаимно перпендикулярных вектора (,, ), то формула для определения модуля равнодействующей () принимает вид:

. (1.11)

Наиболее общим способом определения модуля и направления равнодействующей является аналитический способ, в основе которого лежит тот факт, что проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на координатные оси:

;

; (1.12)

.

где F_ix, F_iy, F_iz - проекции силы F_i на координатные оси;

R_x, R_y, R_z - проекции равнодействующей на те же оси.

Модуль равнодействующей будет равен:

(1.13)

Направление в пространстве можно определить косинусами углов между ортами определяющими направление осей координат, и вектором равнодействующей:

cos()=R_x /R; cos() =R_y/R; cos()= R_z/R. (1.14)

В частном случае, когда все силы расположены в одной плоскости, удобно выбрать систему координат Оху в плоскости расположения сил. Тогда проекции всех сил на ось Oz равны нулю, и выражения (1.12)-(1.14) для определения равнодействующей примут вид:

;

; (1.15)

;

cos ()=R_x /R; cos() =R_y/R

Для равновесия сходящейся системы сил необходимо и достаточно, чтобы ее равнодействующая равнялась нулю:

. (1.16)

Это векторное равенство для решения практических задач удобно использовать в графической и аналитической формах.

Если суммирование векторов производить в графической форме, то при R = 0 конец последней из суммируемых сил должен совпадать с началом первой суммируемой силы; в этом случае говорят, что силовой многоугольник замкнут (рис. 1.26). Это условие удобно использовать при графическом решении задач для плоских систем сил.

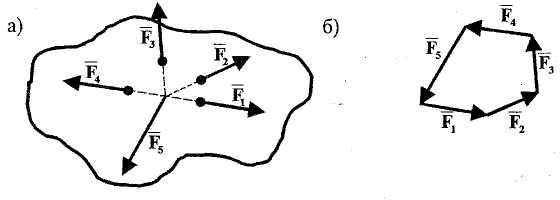
Рис. 1.26

Векторное равенство (1.16) эквивалентно трем скалярным равенствам:

R_x=0;R_y=0;R_z=0. (1.17)

Принимая во внимание равенства (1.12), получаем аналитические условия равновесия, которые при наличии в них неизвестных членов принято называть уравнениями равновесия сходящейся системы сил:

;

(1.18)

;

.

Таким образом, для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из осей координат.

При решении реальных задач перед использованием условия (1.18) необходимо предварительно убедиться, что исследуемая система сил является сходящейся. Это не всегда является очевидным, но если тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то существует теорема, в которой доказывается, что такая система сил всегда сходящаяся.

В задачах статики, как правило, заранее известно, что исследуемое тело находится в равновесии, и требуется определить одну или две из неизвестных сил, под действием которых тело находится в равновесии.

В соответствии со всем ранее изложенным, решение задач на нахождение неизвестных сил из системы сходящихся сил, под действием которых тело находится в равновесии, в графической форме будет можно производить в следующей последовательности:

а) выделяется исследуемое тело;

б) на чертеж наносятся активные силы;

в) связи мысленно отбрасываются, их действие заменяется реакциями связей;

г) обосновывается, что рассматриваемая система сил - сходящаяся;

д) строится замкнутый многоугольник сил;

е) из многоугольника сил определяются неизвестные силы.

Определение неизвестных сил из системы сходящихся сил в аналитической форме можно производить в следующей последовательности:

а) выделяется исследуемое тело;

б) на чертеж наносятся активные силы;

в) связи мысленно отбрасываются, их действие заменяется реакциями связей;

г) обосновывается, что рассматриваемая система сил - сходящаяся;

д) выбирается система координат;

е) составляются уравнения равновесия;

ж) из уравнений равновесия определяются неизвестные силы.

Для определенности решения пространственной задачи на равновесие системы пространственных сил она должна содержать не более трех неизвестных величин (соответственно трем уравнениям равновесия), а для плоской задачи - не более двух. Если неизвестных величин больше, чем уравнений равновесия, то такая задача называется статически неопределимой. Теоретическая механика занимается только статически определимыми задачами.

Пример 1.1. Груз D весом Р=1000Н прикреплен к вертикальной стене при помощи стержней АС и ВС, соединенных между собой и стенкой с помощью шарниров. Углы между стержнями и стеной соответственно равны а =30°, β=60°. Найти силы, действующие на стержни (рис. 1.27,а).

В качестве тела, состояние равновесия которого необходимо исследовать, выберем шарнирный болт С. На него будет действовать одна активная сила - сила тяжести груза Р, направленная вертикально вниз, и силы реакции со стороны стержней АС и ВС.

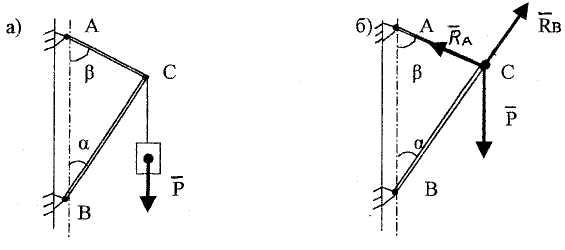
Рис. 1.27

Стержень АС находится под действием растягивающих сил, приложенных к его концам, поэтому сила реакции R_A, действующая со стороны этого стержня на болт С, будет направлена по стержню от болта С. Так как стержень ВС сжимается, сила реакции со стороны этого стержня _В, приложенная к шарнирному болту С, будет направлена от центра стержня к болту С (рис. 1.27,б). Мысленно отбросив связи, получим болт С, находящийся в равновесии под действием сил , _A, _В (рис. 1,28,а). Так как этих сил три, и они расположены в одной плоскости, то данная система сил - сходящаяся.

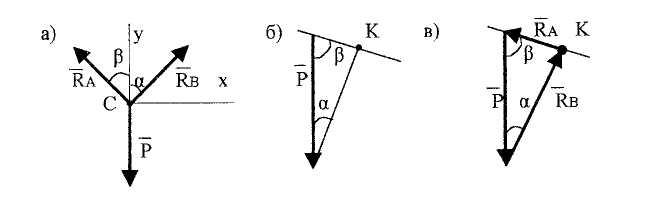
Рис. 1.28

Построение треугольника сил начнем с известной по модулю и направлению силы . Силы _A и _В известны по направлению, но не по модулю. Через начало вектора Р проведем линию действия силы _A , а через конец - прямую, параллельную линии действия силы _В . Точка пересечения этих прямых (К) даст нам конец вектора _В и начало вектора _A (рис. 1.28,б,в). В полученном треугольнике нам известны по модулю сила и углы. Если построение проводилось в определенном масштабе, для определения _A и _В достаточно просто замерить модули векторов на чертежах и умножить на масштаб. Если построение проводилось в произвольной пропорции, для определения модулей векторов _A и _В можно воспользоваться элементарными формулами тригонометрии, получим:

R_В = Рcosa = 866H; R_А =Psina = 500H.

Для использования аналитического условия равновесия при решении данной задачи введем систему координат Сху (рис.1.28,а). Ось Су направим вертикально вверх, ось Сх— вправо, перпендикулярно Су. Составим уравнения равновесия:

∑F_ix= R_В sina- R_А sinβ= 0;

∑F_iу= R_В cosa+ R_А cosβ-Р= 0,

решая которые, найдем:

R_А =500Н, R_В =866Н.

Пример 1.2. Шар веса Р и радиуса г удерживается нитью АВ длиной l на неподвижной гладкой цилиндрической поверхности радиуса R (рис. 1.29,а). Определить натяжение нити Т и давление шара на опорную поверхность, если точка А крепления нити лежит на одной вертикали с центром О цилиндрической поверхности [1].

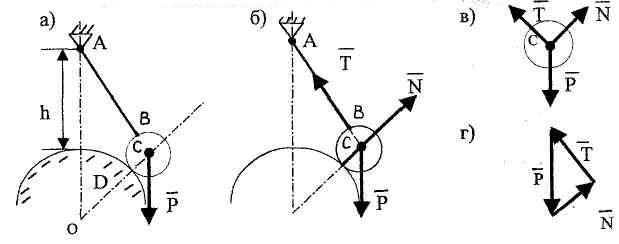
Рис. 1.29

На шар будут действовать активная сила , направленная вертикально вниз, и силы реакций со стороны поверхности и нити. Реакция нити будет направлена по нити от тела. Реакция со стороны поверхности будет лежать на общей нормали шара и поверхности в точке касания. Эта нормаль будет проходить через центр сечения поверхности (точка О), точку касания D и центр шара С (рис. 1.29,а). Так как эта плоская система сил состоит из трех сил, она будет сходящейся. Линии действия сил будут пересекаться в точке С - центре шара. Мысленно отбросим связи. Шар будет находиться в равновесии под действием трех сил , , (рис. 1.29,6). Построив в масштабе замкнутый силовой треугольник ( из конца известной силы проводим прямую, параллельную DC, а из начала силы - прямую, параллельную СА, точка пересечения этих прямых определяет конец силы и начало силы (рис. 1.29,в)), мы можем определить модули сил и с помощью масштаба простым измерением их длин. Если треугольник сил построен не в масштабе, модули сил и легко определить, используя элементарную геометрию. Действительно, из подобия треугольника ОСА и силового треугольника PNT (рис. 1.29,а,в) следует:

==

Отсюда найдем:

N = P; T =P

Пример 1.3. Однородный цилиндр весом Р расположен между двумя гладкими наклонными плоскостями, образующими с горизонтом углы а и β (рис.1.30,а). Определить силы давления цилиндра на обе опорные плоскости [1].

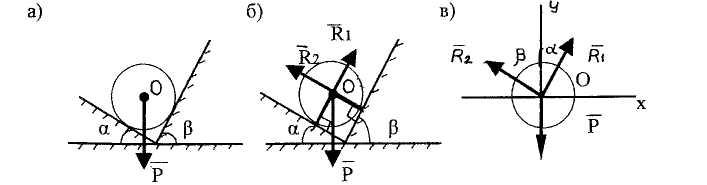
Рис. 1.30

Так как плоскости гладкие, то их реакции ₁ и ₂ (рис. 1.30,6) будут направлены перпендикулярно к плоскостям (к оси цилиндра) и вместе с силой тяжести , направленной вертикально вниз, образуют сходящуюся систему сил. Мысленно отбросим связи. Введем оси координат. Ось Оу направим вертикально вверх, ось Ох - перпендикулярно ей вправо (рис.1.30,в). Запишем уравнения равновесия этой системы сил:

∑F_ix= R₁ sina- R₂ sinβ= 0;

∑F_iу= R₁ cosa+ R₂ cosβ-P= 0,

Отсюда находим:

R₁ = ; R₂ =