НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

ДИСКРЕТНАЯ МАТЕМАТИКА

Методические материалы к решению задач

Раздел I

КОМБИНАТОРИКА

Составитель: проф. Ломакина Л.С.

1999 г.

Сочетания

Задача1. Четыре автора должны написать книгу из 17 глав, причем первый и третий должны написать по 5 глав, второй - 4, а четвертый 3 главы книги. Сколькими способами можно распределить главы между авторами?

Решение:

У множества, состоящего из 17 элементов, существует С⁵ ₁₇ пятиэлементных подмножеств. Поэтому первому автору можно дать главы С⁵ ₁₇ способами. Аналогично из оставшихся 12 глав второй автор может получить 4 главы С ⁴₁₂ способами. Третий автор получает 5 глав С⁵₈ способами, а четвертому достаются оставшиеся 3 главы. Число способов распределения глав равно, следовательно,

С⁵ ₁₇ С ⁴₁₂ С⁵₈ = 171531360

Задача2. Сколько экзаменационных комиссий, состоящих из 7 членов, можно образовать из 14 преподавателей?

Решение:

Очевидно столько, сколько существует семиэлементных подмножеств у четырнадцатиэлементного множества.

14 · 13 · 12 · 11· 10 · 9 · 8 14 · 13 · 12 · 11 · 10 · 9 · 8

С⁷₁₄ = 7! = 7 · 6 · 5 · 4 · 3 · 2 · 1 = 3432

Задача3. В чемпионате страны по футболу (высшая лига) участвуют 18 команд, причем каждые две команды встречаются между собой 2 раза. Сколько матчей играется в течение сезона?

Решение:

В первом круге состоится столько матчей, сколько существует двухэлементных подмножеств у множества, содержащего 18 элементов, т.е. их число равно С²₁₈.

18 · 17

С²₁₈ = 2 = 153

Во втором круге играется столько же матчей, поэтому в течение сезона состоится 306 встреч.

Задача4. Сколькими способами можно расположить в ряд 5 белых и 4 черных шара так, чтобы черные шары не лежали рядом (шары одного цвета не отличимы друг от друга)?

Решение:

Пусть белые шары уложены в ряд, тогда черные шары можно положить по одному на шесть мест: 4 места - между пятью белыми шарами, 2 места - спереди и сзади от белых шаров. Но на шесть мест четыре шара можно положить С⁴₆ способами, так как именно столько существует четырехэлементных подмножеств у шестиэлементного множества. Следовательно, число способов равно

65

С⁴₆ = С²₆ = 2 = 15

Задача5. На первой из двух параллельных прямых лежит 10 точек, на второй - 20. Сколько существует треугольников с вершинами в этих точках?

Решение:

Треугольники могут быть двух видов. У треугольников первого вида одна вершина на первой прямой, две вершины - на второй прямой. Вершину на первой прямой можно выбрать 10 способами, две вершины на второй прямой можно выбрать С²₂₀ способами. Всего, следовательно, существует 10С²₂₀ треугольников первого вида. У треугольников второго вида одна вершина находится на второй прямой, а две другие вершины - на первой. Число таких треугольников подсчитывается аналогично. Оно равно 20С²₁₀. Таким образом, искомое число всех треугольников

20  19 10  9

10  С²₂₀ + 20  С²₁₀ = 10 2 + 20 2 = 100 (19 + 9) = 2800

Задача6. Из группы, состоящей из 7 мужчин и 4 женщин, надо выбрать 6 человек так, чтобы среди них было не менее 2 женщин. Сколькими способами можно это сделать?

Решение:

Можно выбрать двух, трех или четырех женщин. Поскольку нас интересует лишь состав элементов в комбинации, а не порядок элементов, то используем формулу для числа сочетаний.

Таким образом, двух женщин можно выбрать C ²₄ способами. После этого надо выбрать 4 мужчин, что можно сделать C ⁴₇ способами. По правилу произведения получаем C ²₄C ⁴₇ способов. Аналогично, выбирая 3 женщин и 3 мужчин, получают C ³₄C ³₇ способов, а выбирая 4 женщин и 2 мужчин, получают C ⁴₄C ²₇ способов.

По правилу суммы всего

C ²₄C ⁴₇ + C ³₄C ³₇ + C ⁴₄C ²₇=371 способ.

Задача7. Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?

Решение:

Белые шашки можно расставить С ¹²₃₂ способами. После выбора 12 полей для белых шашек остается 32-12=20 полей для черных шашек, на которые их можно поставить С ¹²₂₀ способами. Всего по правилу произведения С ¹²₃₂С ¹²₂₀ способов.

Задача8. Даны n точек на плоскости, никакие три из которых не лежат на одной прямой и никакие 4 - на одной окружности. Через каждые две из этих точек проводится прямая, а через каждые три - окружность. Найти наибольшее число точек пересечения всех проведенных прямых со всеми окружностями.

Решение:

n точек определяют С ³_n окружностей. Из их числа С ²_n-1 проходят через данную точку и С ¹_n-2 - через данные две точки. Поэтому прямая, проходящая через две данные точки, имеет не более

2 С ³_n-2+(2C ²_n-1 - C ¹_n-2)+2 точек пересечения с окружностями. Так как через n точек проходит C ²прямых, то имеем не более чем

C ²_n[2C ³_n-2+2C ²_n-1 - C ¹_n-2+2] точек пересечения.

Задача 9. Сколькими способами можно выбрать 5 делегатов из состава конференции на которой присутствуют 15 человек?

Решение:

Так как порядок выбора значения не имеет и делегаты не повторяются, то число способов будет сочетаниями без повторений. Значит

С(15,5) =

Задача 10. Сколькими способами можно попасть из точки А в точку С, если можно двигаться лишь в право и вверх по отрезкам сети?

D C

A B

Решение:.

Каждый путь состоит из 8 горизонтальных и 4 вертикальных единичных отрезков. Если обозначить горизонтальный отрезок буквой а, а вертикальный - буквой х, то получим множество из 8 букв а и 4 букв х. Согласно примеру 2 число таких множеств, а тем самым и искомое путей равно:

С(12,4) = .

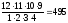Задача 11. Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта пирожных.

Решение:

. Искомое число равно

V(7,4) = C(7+4-1,4) =

Задача 12. В почтовом отделении продаются открытки 10 сортов. Сколькими способами можно купить в нем 12 открыток?

Решение:

. Искомое число равно

V(12,10) = C(12+10-1,10) =

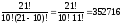
Задача 13. Каждый из десяти радистов пункта А старается установить связь с каждым из двадцати радистов пункта В. Сколько возможно различных исходов такой связи?

Решение:

. Рассмотрим сначала число различных исходов связи одного радиста. Каждый радист пункта А пытается установить связь с двадцатью радистами пункта В, и результат связи с каждым из них будет либо нулем (связи нет), либо единицей (связь установлена). Значит, числом исходов связи одного радиста будет число сочетаний без повторений из 2 по 20 (т.е. 2²⁰). Теперь рассмотрим всех радистов. У каждого из них будет 2²⁰ исходов связи. Следовательно числом различных исходов связи у всех радистов будет число сочетаний без повторений из 2²⁰ по 10. Получим (2²⁰)¹⁰ = 2²⁰⁰.