Перестановки

Задача 1. Сколько шестизначны&&х чисел, кратных пяти, можно составить из цифр 1,2,3,4,5,6 при условии, что в числе цифры не повторяются.

Решение:

Для того, чтобы число, составленное из заданных цифр, делилось на 5, необходимо и достаточно, чтобы цифра 5 стояла на последнем месте. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Следовательно, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов, т.е. 5! = 5* 4* 3*·2* 1 = 120.

Задача 2. Сколько различных перестановок можно образовать из букв слова “молоко”?

Решение:

Образовать какую-либо перестановку из букв слова “молоко” - это значит на шесть занумерованных мест каким-нибудь образом поставить одну букву “м”, одну букву “л”, одну букву “к” и три буквы “о”. Если буквы “м”, “л” и “к” как-то поставлены, то остальные места заполняются буквами “о”. Но сколькими способами можно поставить три различные буквы на шесть мест? Очевидно, что число способов равно числу всех трехэлементных упорядоченных подмножеств шестиэлементного множества, т.е. равно А³₆ = 6 · 5 · 4 = 120

Задача 3. Для дежурства в классе в течение недели (кроме воскресенья) выделены 6 учащихся. Сколькими способами можно установить очередность дежурств, если каждый учащийся дежурит один раз?

Решение:

Требуется найти число всех перестановок из шести элементов (число всех возможных перестановок дежурных класса, т.е. Р₆

Р₆ = 6! = 720

Задача 4. Четыре автора должны написать книгу из 17 глав, причем первый и третий должны написать по 5 глав, второй - 4, а четвертый 3 главы книги. Сколькими способами можно распределить главы между авторами?

Решение:

Занумеруем для удобства главы арабскими цифрами, а авторов - римскими. Представим в виде следующей таблицы один из способов распределения глав:

I	II	III	IV
2, 4, 8, 11, 14	1, 5, 7, 13	9, 10, 15, 16, 17	3, 6, 12

Любая перестановка чисел второй строки будет приводить к новому распределению, если только она не сводится к перестановке чисел внутри столбцов. Так как всего существует 17! способов перестановки чисел второй строки, а любые перестановки чисел внутри столбцов (их соответственно 5!, 4!, 5!, 3!) не дают новых способов, то искомое число способов распределения глав

17! .

(5!)²  4!  3! = 171531360

Задача 5. Известно, что крокодил имеет не более 68 зубов. Доказать, что среди 16¹⁷ крокодилов может не оказаться двух крокодилов с одним и тем же набором зубов.

Решение:

Подсчитаем максимальное число крокодилов с неодинаковым набором зубов. Очевидно, что их число равно числу всех подмножеств у 68-элементного множества, т.е. равно 2⁶⁸. Так как 16¹⁷ = 2⁶⁸, то 16¹⁷ крокодилов могут иметь различные наборы зубов. Ясно, что если крокодилов более 16¹⁷ особей, то среди них обязательно найдутся по крайней мере два с одним и тем же набором зубов.

Задача 6. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами их можно посадить в два ряда, чтобы рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?

Решение:

Исходя из условия задачи имеем, что ученики сидят в два ряда, по шесть человек в каждом, и у каждого ряда свой вариант. Значит, число способов будет складываться из числа перестановок в каждом ряде (т.е. 6!). Но при каждом раскладе этих перестановок два любых ученика могут поменяться рядами, а это число размещений с повторениями из 6 по 2 (т.е. 6²). Значит, число способов уже стало (6!)². Также необходимо учесть, что эти два ряда можно поменять местами, следовательно число способов удвоится - 2*(6!)².

Это и будет необходимое на число способов.

Задача 7. Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд, так чтобы при этом два футболиста одной команды не стояли рядом?

Решение.

Воспользоваться алгоритмом предыдущей задачи мы не можем, так как в прошлой задаче нас не интересовало сколько человек пересело с одного ряда на другой. Здесь же строго определено, что два игрока одной команды рядом стоять не могут. Значит, игроки двух команд чередуются, и единственный способ изменить их строй, это поменять местами игроков одной команды. Игроки одной из команд могут встать 11! способами. При каждом из этих способов игроки другой команды также могут встать 11! способами. Следовательно, общее число размещений игроков двух команд будет (11!)*(11!) или (11!)². Но ведь расчет игроков в строю можно вести и обратный (т.е. последний игрок будет считаться первым, предпоследний - вторым и т.д.), значит число размещений должно быть удвоено. И конечный результат будет равен 2*(11!)²

Задача 8. Требуется составить расписание отправления поездов на различные дни недели. При этом необходимо, чтобы: 3 дня отправлялись по 2 поезда в день, 2 дня - по 1 поезду в день, 2 дня - по 3 поезда в день. Сколько можно составить различных расписаний?

Решение:

Количество поездов, отправляемых в день (числа 1,2,3), - это три группы одинаковых элементов, из которых должна быть составлена выборка. При этом в расписании на неделю число 1 повторяется 2 раза, число 2 повторяется 3 раза и число 3 повторяется 2 раза. Число различных расписаний равно

P(2,3,2)= 7!/(2!*3!*2!)=210.

Задача 9. На полке находятся m + n различных книг, из которых m в черных переплетах, а n в красных. Сколько существует перестановок этих книг, при которых книги в черных переплетах занимают первые m мест? Сколько положений, в которых все книги в черных переплетах стоят рядом?

Решение:

Книги в черных переплетах можно переставить m! способами, а в красных - n! способами. Всего по правилу произведения m!n! способов. Если книги в черных переплетах стоят рядом, то надо еще выбрать для них между книгами в красных переплетах. Это можно сделать n+1 способами. Всего получаем

m!n!(n+1)=m!(n+1)! способов.

Задача 10. Сколькими способами можно переставить буквы слова «кофеварка» так, чтобы гласные и согласные буквы чередовались?

Решение:

Так как согласных букв на одну больше, чем гласных, то при нужной перестановке первая и последняя буквы должны быть согласными. Согласные можно переставить P(2,1,1,1)способами, а гласные - P(2,1,1)способами. Всего по правилу произведения имеем

P(2,1,1,1)*P(2,1,1)=720 способов.

Задача 11. Сколькими способами можно обить 6 стульев тканью, если имеются ткани шести цветов и все стулья должны быть разного цвета?

Решение:

Пронумеруем стулья числами 1, 2, ... , 6 и обозначим ткань для к-го стула через х_к. Тогда (х₁ ,... ,х₆) - перестановка из цветов материй, причем каждой такой перестановке соответствует один и только один способ размещения. Значит число способов равно P(6) = 6! = 720.

Задача 12. Сколькими способами могут расположиться в турнирной таблице 10 команд, если известно, что никакие две команды не набрали поровну очков?

Решение:

Так как каждой перестановке соответствует один и только один способ размещения, то число способов будет перестановками без повторений. Следовательно: Р(10) = 10! = 3628800.

Задача 12. Сколькими способами можно разложить 28 различных предметов по четырем различным ящикам, так, чтобы в каждом ящике оказалось по 7 предметов?

Решение: Пометим все ящики цифрами 1, 2, 3, 4. Тогда число различных раскладок равно Р(7, 7, 7, 7). Т.е. число способов является перестановками с повторениями.

P(7, 7, 7, 7) =

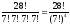
Задача 13. Сколькими способами можно положить 28 различных открыток в 4 одинаковых конверта так, чтобы в каждом конверте лежало по 7 открыток.

Решение:

Также пронумеруем все конверты. Число способов раскладки будет Р(7, 7, 7, 7). Но конверты все одинаковые, поэтому их можно менять местами, не меняя результат раскладки. Так как число различных перестановок четырех конвертов равно Р(4) = 4!, то число различных раскладок уменьшится в 4! раз и станет равно: .

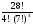Задача 14. Сколько слов можно получить, переставляя буквы в слове «математика»?

Решение:

Слово математика является множеством длины 10, имеющим состав (2, 3, 2, 1, 1, 1) (буква ‘м’ входит два раза, буква ‘а’ - три раза и т.д.). Значит, при перестановках букв получится

Р(2, 3, 2, 1, 1, 1) = .