
- •§8. Пространство геометрических векторов, как пример линейного пространства
- •1О. Направленные отрезки.
- •2О. Размерность линейных пространств геометрических векторов.
- •3О. Проекции вектора на ось
- •40. Скалярное произведение векторов.
- •5О. Векторное и смешанное произведения векторов.
- •60. Выражение векторного и смешанного произведения векторов через координаты сомножителей
- •70. Двойное векторное произведение.
- •80. Примеры решения задач.
60. Выражение векторного и смешанного произведения векторов через координаты сомножителей
Пусть в пространстве
векторов задан произвольный базис
![]() .
Пусть
.
Пусть
![]() заданы своими координатами в этом
базисе, т.е.
заданы своими координатами в этом
базисе, т.е.
![]() .
.
Тогда
 Так
как
Так
как
![]() ,
то получаем
,
то получаем
![]()
В частности, если
базис – ортонормированный, т.е.
![]() то в силу
то в силу
![]() ,
получаем
,
получаем
![]()
Это равенство формально можно переписать в виде
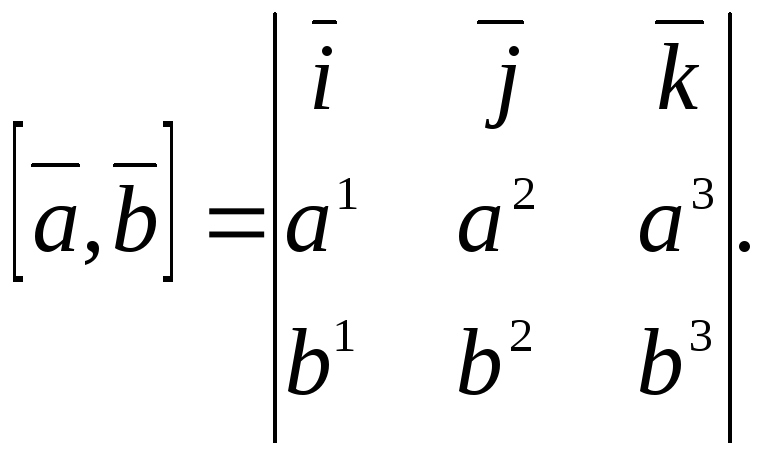
Если ввести в
рассмотрение третий вектор
![]() и вычислить смешанное произведение
векторов, то получаем:
и вычислить смешанное произведение
векторов, то получаем:

с учетом свойства равенства нулю смешанного произведения компланарных векторов. Отсюда следует, что
![]()
или, формально можно записать
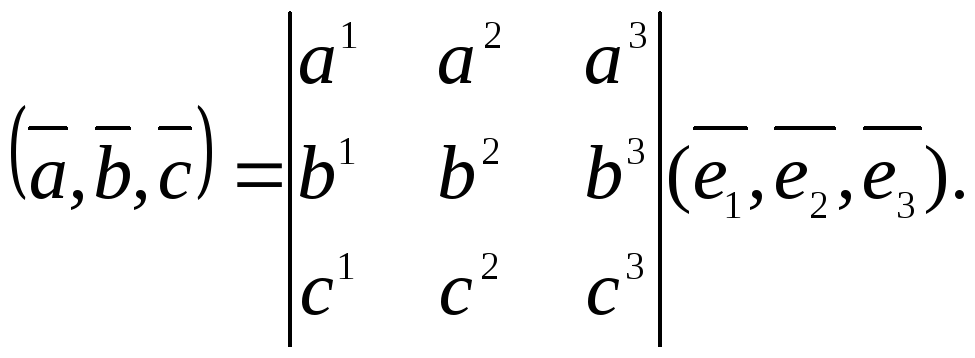
Если рассматриваемый
базис ортонормированный, то
![]()
70. Двойное векторное произведение.
Определение
18. Двойное
векторное произведение векторов
![]() ,
,
![]() ,
,
![]() это произведение вида
это произведение вида
![]() .
.
Выразим двойное векторное произведение через скалярное.
Пусть
![]()
![]()
![]() и
и
![]()
![]() .
Тогда, в силу
.
Тогда, в силу
![]()
![]()
![]() лежит в плоскости векторов
лежит в плоскости векторов
![]() и
и
![]()
![]() .
Умножим это равенство скалярно на
.
Умножим это равенство скалярно на
![]() .
Имеем
.
Имеем
![]() .
.
Пусть
вектор
![]() не перпендикулярен одновременно векторам
не перпендикулярен одновременно векторам
![]() и
и
![]() (в противном случае
(в противном случае
![]() в обоих случаях). Тогда
в обоих случаях). Тогда
![]()
![]()
![]() ,
такое что
,
такое что
![]() ,
,
![]() .
.
Тогда
![]() .
.
Для
того, чтобы найти
![]() ,
вычислим левую и правую части в некотором
базисе. Пусть вектор
,
вычислим левую и правую части в некотором
базисе. Пусть вектор
![]() направлен вдоль вектора
направлен вдоль вектора
![]() ,
,
![]() лежит в плоскости векторов
лежит в плоскости векторов
![]() и
и
![]() ,
,
![]() определяется из условия, что
определяется из условия, что
![]() ,
,
![]() ,
,
![]() образуют правую тройку. Тогда
образуют правую тройку. Тогда
![]() ,
,
![]() ,
,
![]() .
.
Имеем
 ,
,
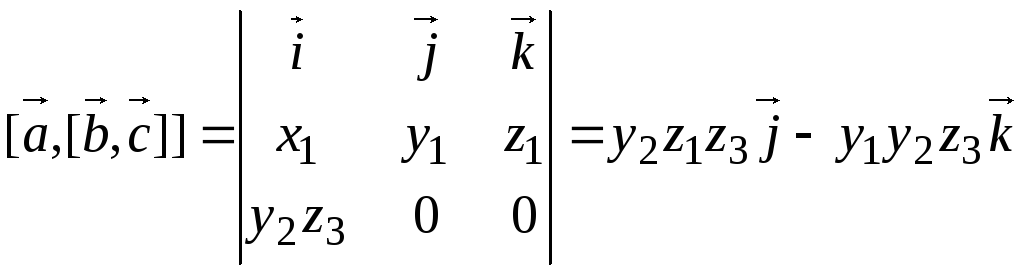 .
.
![]() .
.
![]() .
.
Отсюда
видно, что
![]() .
Итак, справедлива формула:
.
Итак, справедлива формула:
![]() .
.
Пример 1. Доказать тождество Якоби:
![]() .
.
Имеем
![]() ,
,
![]() ,
,
![]() .
.
Суммируя эти равенства, получим тождество Якоби.
Пример
2. Вычислить
![]() .
.
Имеем:
(![]() )
)
![]()
![]() .
.
80. Примеры решения задач.
Пример
1. Вычислить
синус угла между векторами
![]() ,
,
![]() .
.
Имеем:
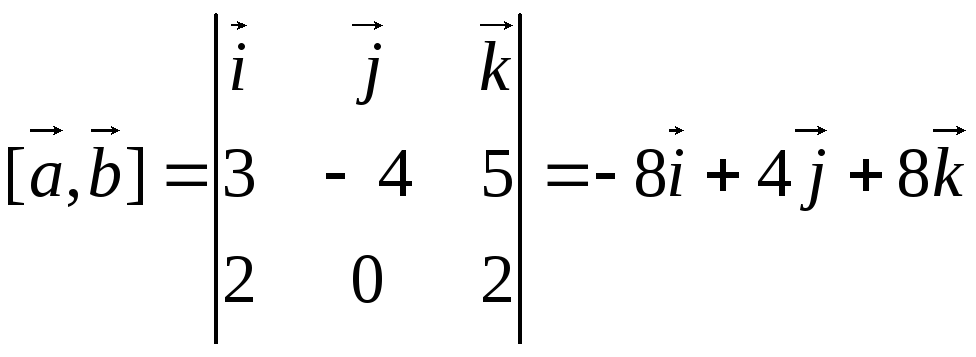 .
.
![]() .
.
![]() .
.
Пример
2. Так как
модуль векторного произведения численно
равен площади параллелограмма,
построенного на перемножаемых векторах,
то если
![]() ,
,
![]() .
.
Имеем
![]() .
.
Если
параллелограмм расположен в плоскости,
то
![]() и
и
![]() .
.
П
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
Имеем
.
Имеем
![]()
![]()

![]()

![]()
![]()

 .
Но
.
Но
![]()
![]()
![]()
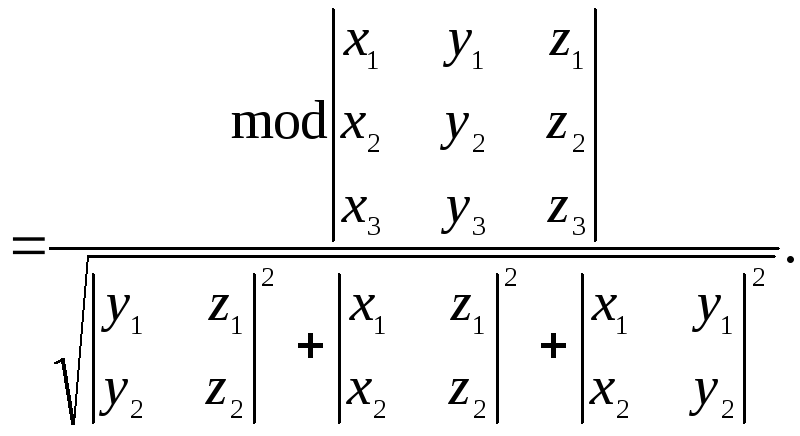 .
.
