(Весна 2012). Лабораторные работы по теме «Задача коммивояжера. Элементы метода ветвей и границ. Простые эвристики» Задача коммивояжера
Задача коммивояжёра (коммивояжёр — бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.
Существует несколько частных случаев общей постановки задачи, в частности геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.
Общая постановка задачи, впрочем как и большинство её частных случаев, относится к классу NP-сложных задач.
Ветви и границы
Метод ветвей и границ - вариант бэктрэкинга.
При бэктрэкинге, когда частичный вектор не удовлетворяет ограничениям, этот вектор и все его потомки исключаются из поиска.
Если приписать большую стоимость недопустимым векторам и нулевую стоимость допустимым векторам, то мы должны искать вектор минимальной стоимости. Во многих случаях частичным векторам можно естественным образом приписать стоимости, удовлетворяющие соотношению:
стоимость(x1, x2,…, xn) ≤ стоимости (x1, x2,…, xn)
для всех возможных значений переменных.
Идея метода ветвей и границ
Мы не производим ветвления в круглом узле, стоимость которого выше, чем минимальная стоимость найденных до сих пор решений. Эта граница обновляется, когда находиться лучшее решение.
Обходим дерево решений методом поиска в глубину и запоминаем решение VX наименьшей стоимости. Когда стоимость частичного вектора VY превышает стоимость VX, все потомки VY исключаются. Если находиться лучшее решение VZ, его стоимость становится новой границей.
Для задачи максимизации все делается точно наоборот. Ветвление в круглом узле не производится, если значение в нем меньше, чем максимальное из значений найденных решений.
Алгоритм метода ветвей и границ
Метод ветвей и границ применяется для каждого маршрута для нахождения оптимального пути.
Приведение матрицы расстояний
В любой маршрут входит один элемент каждой строки и каждого столбца матрицы расстояний. Поэтому если из всех элементов некоторой строки вычесть одно и то же число, то в новой матрице длины всех маршрутов уменьшатся на это число по сравнению со старой матрицей. То же можно сказать и о столбцах матрицы расстояний. Эти свойства объясняются тем, что из каждого города мы должны один раз уйти и в каждый город один раз прийти. Поэтому найдем
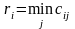(2.2)
и образуем новую матрицу:
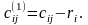(2.3)
В
матрице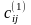
найдем
наименьший элемент в каждом столбце
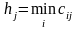(2.4)
и построим матрицу:
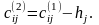(2.5)
Тогда
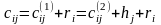(2.6)
Матрица
—
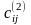приведенная
матрица расстояний,
—
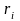константа приведения по строкам,
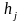— константа приведения по столбцам.
Матрица
имеет
хотя бы один ноль в каждой строке и в
каждом столбце.
Пусть z – некоторый маршрут, тогда
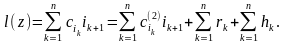(2.7)
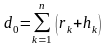(2.8)
Если обозначить
через
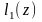длину маршрута коммивояжера в матрице
расстояний
и
воспользоваться (2.8), то получим
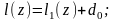так
как
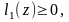то
,
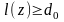т.е. длина любого маршрута оценивается
снизу числом
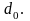
Если
после применения процедуры приведения
в каждой строке и
в каждом столбце есть ровно один нуль,
то мы решили задачу о назначении.
Величина целевой функции равна
,
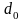а нули указывают назначение.
Если нули образуют единственный цикл,
то мы решили задачу
о коммивояжере, и длина кратчайшего
маршрута равна
Ветвление
Рассмотрим
некоторый маршрут, который содержит
переход из точки i
в
точку j.
Для длины этого маршрута имеет место
неравенство
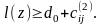
Для
переходов, у которых
,
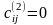получаем, что
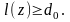Естественно
предположить, что кратчайший путь
коммивояжера содержит один
из нулевых переходов.
Обозначим
через
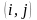множество маршрутов, содержащих переход
из i
в j
непосредственно
и через
—
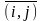множество маршрутов, не содержащих
такой переход,
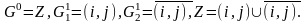Таким образом, множество
Z
разбивается на два подмножества (рис.
2.1). Как
известно, ветвление на два подмножества
называется дихотомическим.
Рис. 2.1
Рассмотрим
нижнюю оценку для множества маршрутов
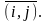Для
оценка
остается
.
Для всех маршрутов из
из
точки
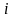нужно уйти в точку
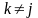и
в точку
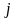прийти
из точки
,
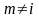поэтому
имеем
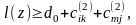
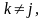
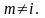
Поскольку
выход из точки
добавляет
к оценке по крайней мере наименьший
элемент строки
,
а вход в точку
—
по крайней мере наименьший
элемент столбца
,
то
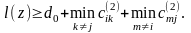
Для каждого нулевого перехода может быть вычислена величина
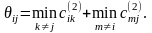(2.9)
Для
вычисления
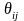для
нулевого перехода нужно найти минимальные
элементы в строке и столбце, пересекающихся
на этом переходе
(минимумы находятся без учета
рассматриваемого нулевого перехода
)
и
полученные минимумы сложить.
В
качестве перехода, используемого для
разветвления, выбирается
тот, у которого значение
максимально,
.
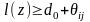Находим
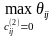и
этот переход выбираем в качестве того,
по которому происходит
разветвление. Это связано с тем, что
необходимо получить по возможности
большую оценку для множества
.
В
матрице, соответствующей множеству
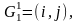вычеркиваем
строку
и столбец
и положим
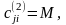чтобы
предотвратить появление цикла
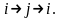Полученную
матрицу можно привести; пусть сумма
констант приведения равна
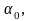тогда
для
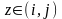получим
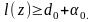
В
матрице, соответствующей множеству
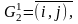следует
положить
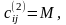и для
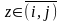получим
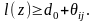
Если
эту матрицу привести и сумма констант
приведения равна
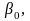то
для
получаем
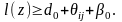
Модифицируем
список множеств, не подвергшихся
разбиению. Вместо множества
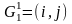записываем множества
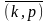и
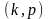и
полученные множества переобозначаем: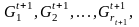
где
t=1.
Удаляем (или отмечаем) множества,
отсеянные по правилам отсева, и переходим
к множеству
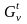с наименьшей нижней оценкой
,
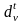положив t
равным t+1.
В результате применения описанного выше алгоритма получаем дерево ветвления в виде рис. 2.2
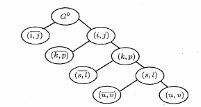
Рис 2.2