40. Скалярное произведение векторов.

Определение 14. Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Таким образом, если , – вектора, то скалярное произведение обозначается и

.

Свойства скалярного произведения.

1) Коммутативность: .

Действительно, (так как , то есть четная функция, то ) .

2) Скалярное произведение двух векторов равно длине одного вектора умноженной на проекцию другого на направление первого.

Действительно, .

Отсюда видно, что если , то .

Следовательно, проекция вектора на ось равна скалярному произведению этого вектора на направляющий вектор оси.

3) .

Действительно, .

4) .

Действительно, .

5) Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.

Пусть     .

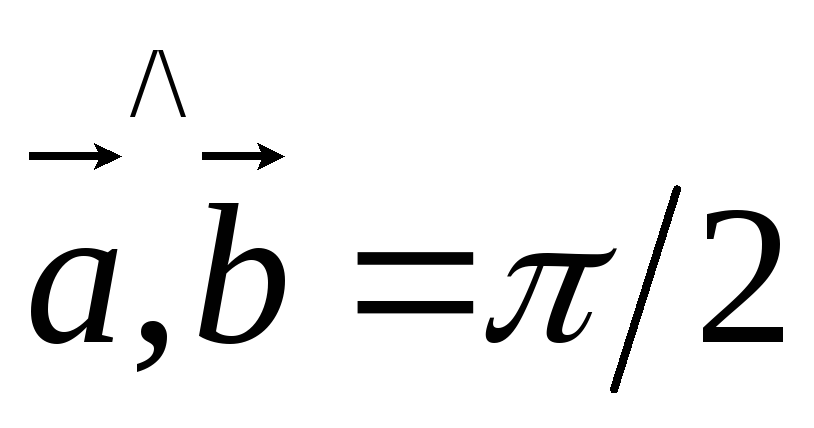
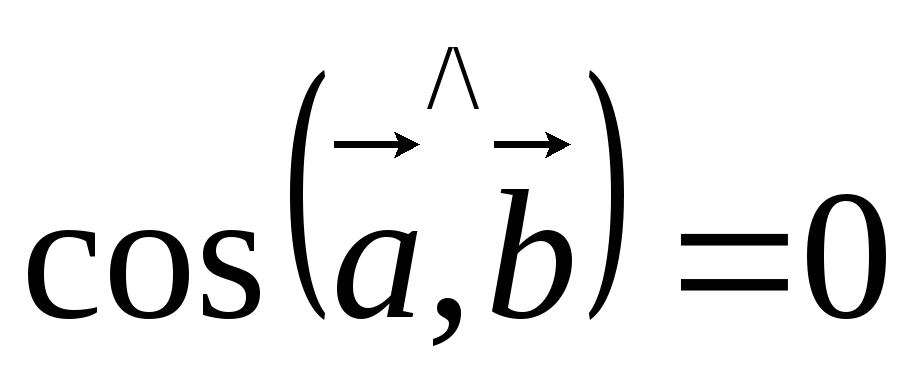
Пусть 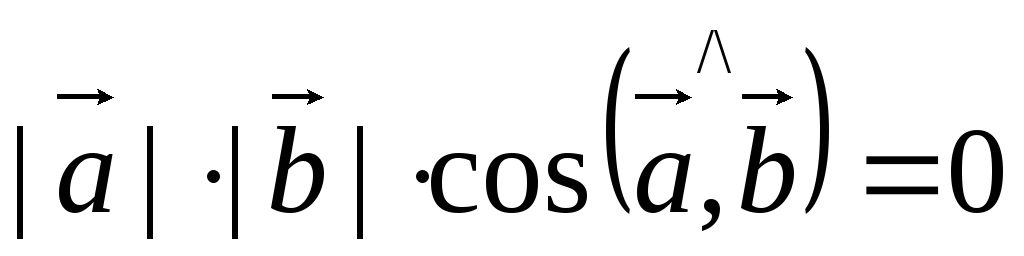 , так как ,    .

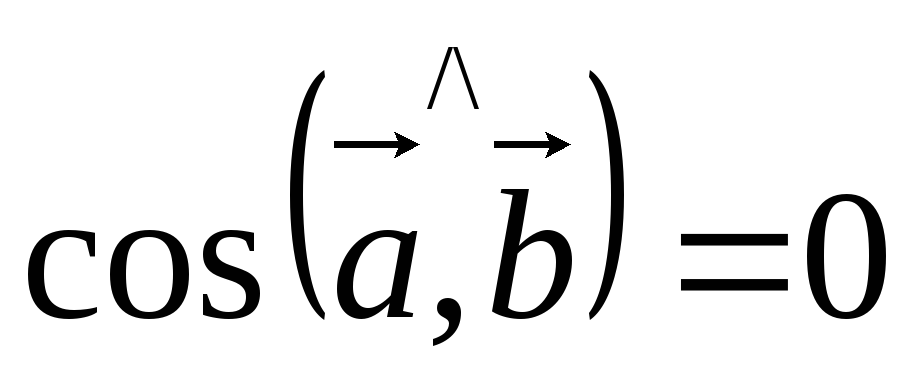
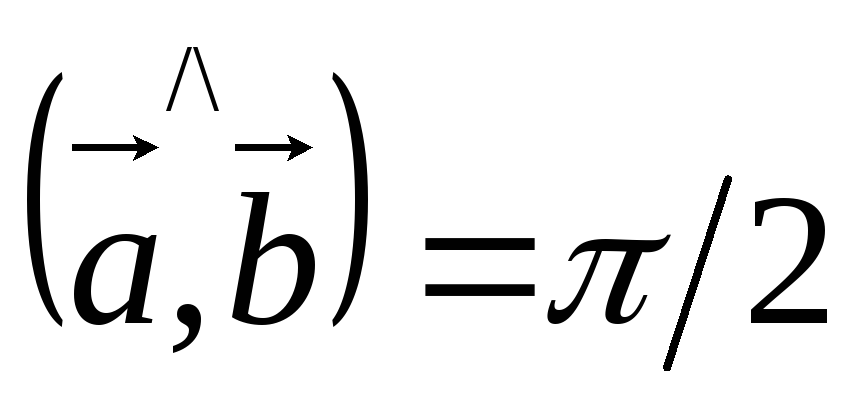
6) Пусть  , т.е.  скалярный квадрат вектора равен квадрату длины вектора  .

Из последнего свойства следует, что – отдельная строка.

7) Пусть в пространстве геометрических векторов задан ортонормированный базис т.е. Тогда

Если вектора заданы своими координатами , то

т.е. в прямоугольной декартовой системе координат скалярное произведение векторов равно сумме произведений соответствующих координат.

Из свойства 7) вытекают некоторые метрические формулы:

1)  

2) Если , то , , .

Таким образом, прямоугольные координаты вектора есть его ортогональные проекции на оси прямоугольной системы координат.

3. Пусть , 

.

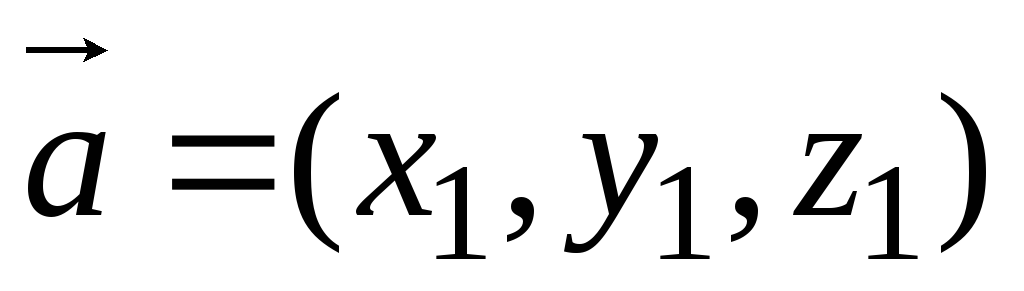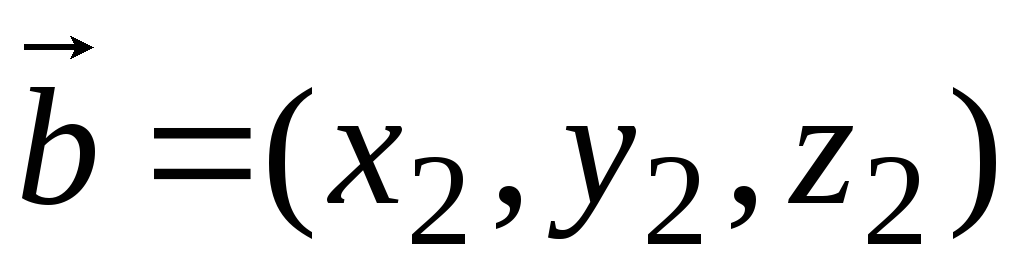
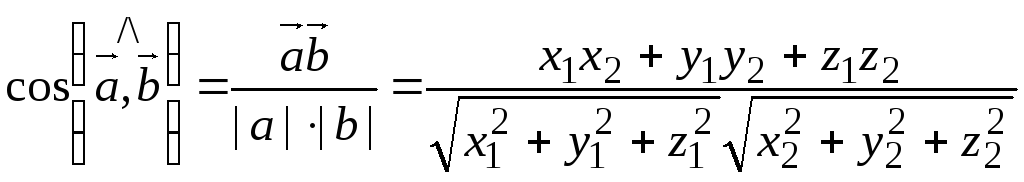Таким образом,   .

Из формулы косинуса угла между векторами легко найти углы , , , которые вектор образует с осями координат. Эти углы называются направляющими углами.

Имеем:

, , .

, , называются направляющими косинусами вектора . Они связаны соотношением

.

Следовательно, вектор есть координаты вектора , то есть вектора и .

.

5О. Векторное и смешанное произведения векторов.

Определение 15. Упорядоченная тройка некомпланарных векторов называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройка называется левоориентированной или левой.

Рис. 10. Ориентированные тройки векторов

а) Правая тройка б) Левая тройка

Определение 16. Векторным произведением двух векторов и называется вектор , удовлетворяющий условиям:

1. .

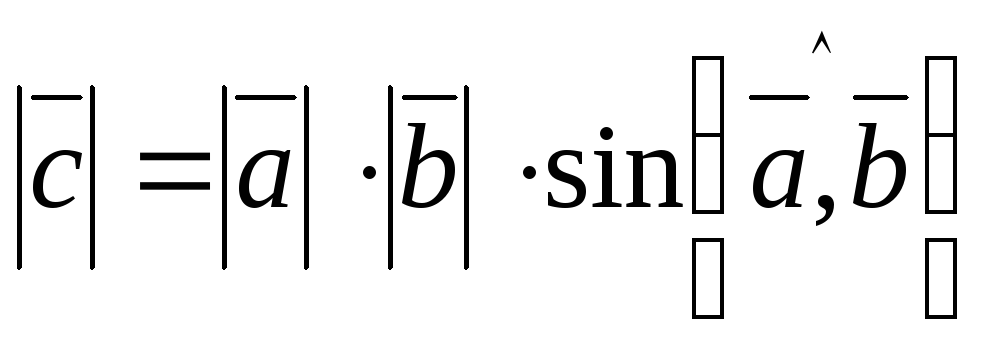2. вектор ортогонален векторам и .

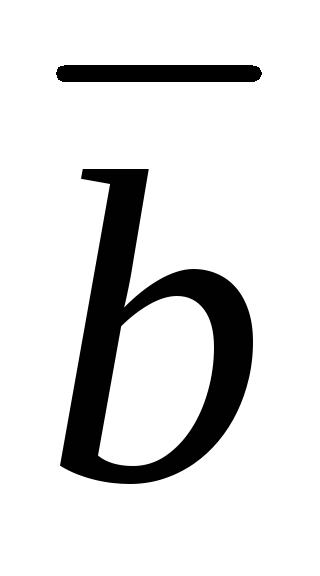3. вектора образуют правую тройку векторов.

Обозначение:

Свойства векторного произведения

1. Длина вектора численно равна площади параллелограмма, построенного на векторах и .

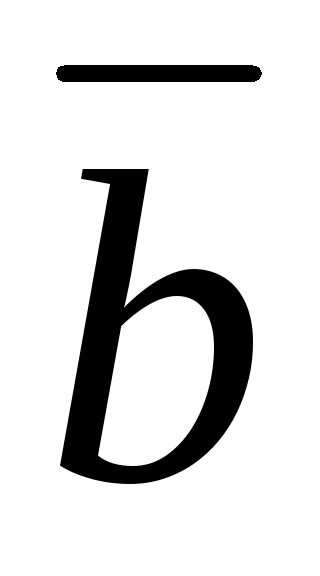Доказательство следует из определения 16.

2. Векторное произведение векторов равно нулю тогда и только тогда, когда сомножители коллинеарны.

Доказательство аналогично свойству 5 скалярного произведения.

3. Векторное произведение антикоммутативно, т.е.

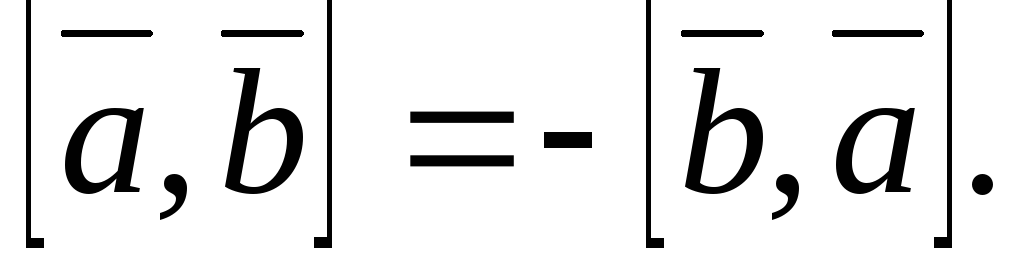
Доказательство.

Тройка – правая, – левая. Тройка будет правой, если изменить направление , т.е. ∎

Пример. Если – правая тройка, то

Далее базис всегда будем рассматривать правый.

4. .

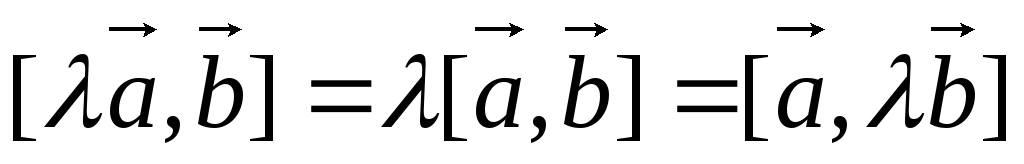Докажем первое равенство.

1. В начале покажем равенство модулей.

.

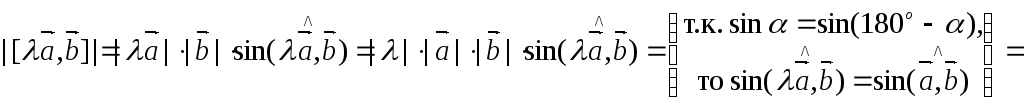
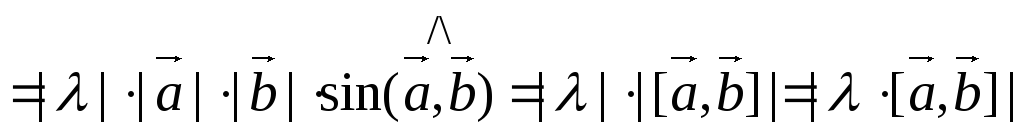2. Так как ||, то .

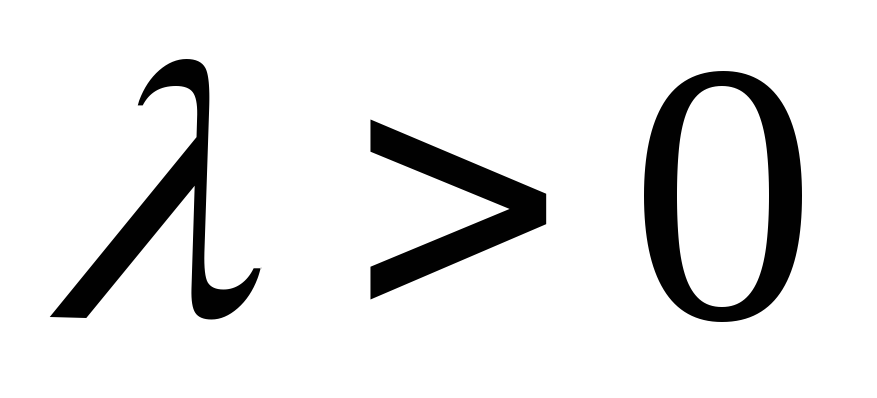3. Покажем, что . Рассмотрим случай и .

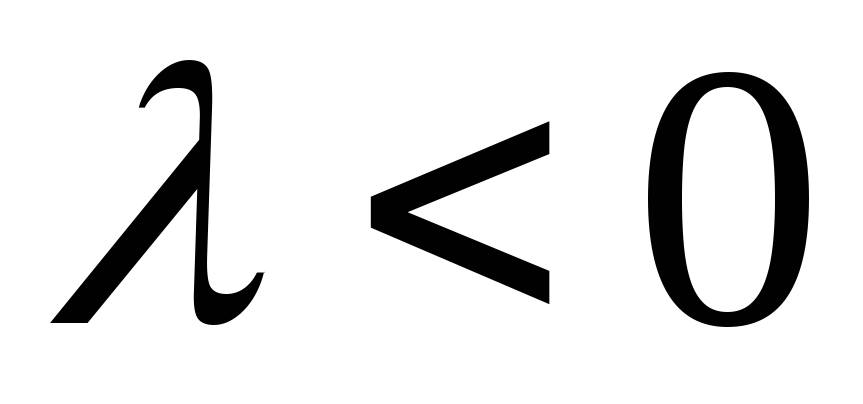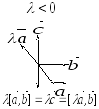
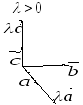
Отсюда вытекает доказываемое свойство.

Определение 17. Смешанным произведением векторов называется число

Обозначение:

Свойства смешанного произведения

1. Смешанное произведение некомпланарных векторов 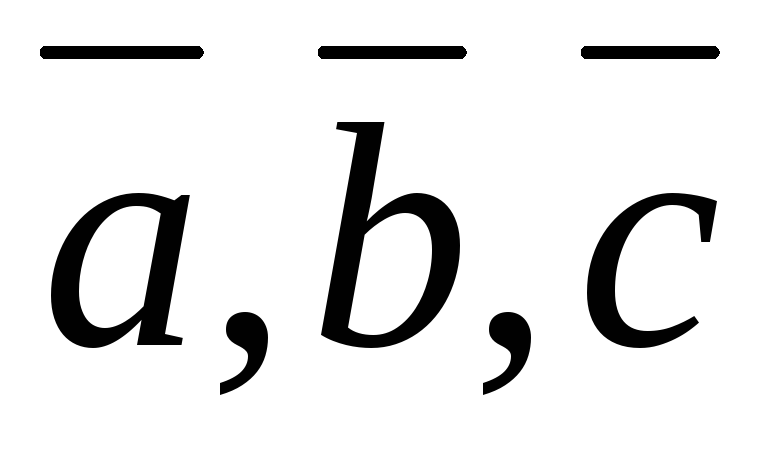по модулю равно объему параллелепипеда, построенного на сомножителях. Оно положительно, если тройка 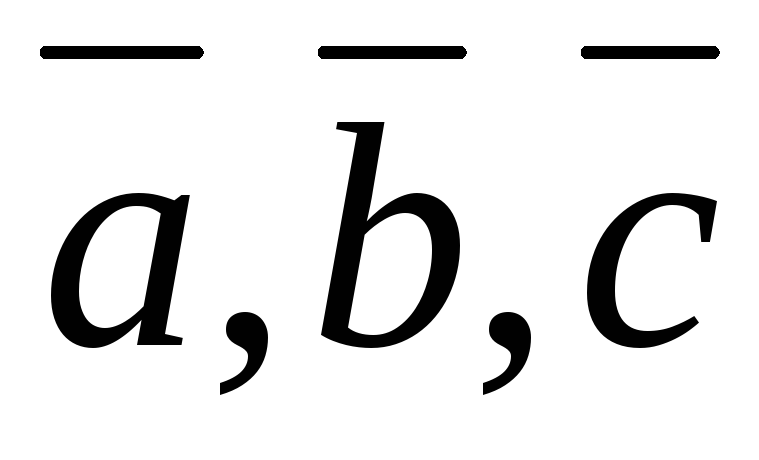правая, и отрицательно, если она левая.

Доказательство.

Действительно, объем параллелепипеда, построенного на векторах равен произведению площади основания на высоту где – угол между и

Поэтому

Знак смешанного произведения совпадает со знаком и поэтому, смешанное произведение положительно, когда направлен с в одну сторону от плоскости векторов т.е. тройка – правая. Аналогично, смешанное произведение левой тройки векторов отрицательно. ∎

2. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.

Доказательство. Если один из векторов нулевой, то свойство очевидно.

Пусть , ,  0.

Пусть , , – компланарны. Тогда  .

Пусть  либо , либо .

В первом случае это означает, что вектор  векторам , ,  , , – компланарны. Во втором случае – ||  и – линейно зависимы  , , – компланарны.

3. Смешанное произведение не зависит от группировки сомножителей, т.е. .

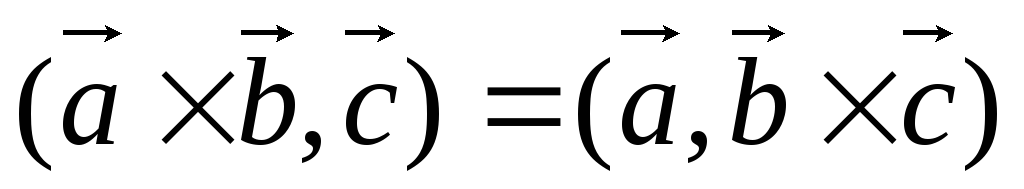Доказательство. Тройки , , и , , ориентированы одинаково, значит знак смешанного произведения одинаковый. Модуль так же одинаковый в силу свойства 1.

Обозначение. Смешанное произведение векторов , , обозначается .

4. .

Следует из свойства циклической перестановки ориентированных векторов.

5. , .

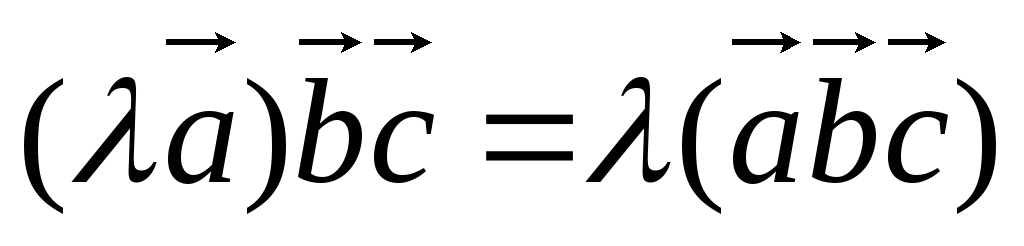Следует из свойств скалярного произведения.

Теорема 5 (линейность векторного произведения). Для любых векторов и любых чисел  и  имеет место равенство:

Доказательство. Воспользуемся линейностью смешанного произведения по второму сомножителю:

Выбирая вместо вектора ортонормированного базиса, можно видеть, что координаты векторов и равны, а значит, равны эти вектора. ∎