
- •1. Символы исчисления высказываний и определение формулы исчисления высказываний.
- •2. Определение доказуемой формулы и система аксиом исчисления высказываний.
- •Рассмотрим примеры получения доказуемых формул.
- •3. Правила вывода доказуемых формул из аксиом.
- •Правило подстановка схематически запишется так
- •4. Производные правила вывода.
- •5. Определение формулы, выводимой из совокупности формул h.
- •6. Понятие вывода из конечной совокупности формул h.
- •7.Проблемы аксиоматического исчисления высказываний
- •8. Понятие и определение предиката.
- •9. Логические и кванторные операции над предикатами.
- •10. Символы и определение формулы логики предикатов.
- •11. Основные равносильные формулы логики предикатов.
- •12. Предваренная нормальная форма формул логики предикатов.
- •13.Общезначимость и выполнимость формул.
- •14. Прямая, обратная и противоположные теоремы.
- •15. Понятие алгоритма и его уточнения.
- •16. Машина Тьюринга и ее функционирование. Тезис Тьюринга.
- •17. Сложноть алгоритмов. Временная и пространственная сложности алгоритмов. Полиномиальные и экспоненциальные алгоритмы.
- •18. Понятие о вычислимых, всюду определенных, частичных и частично- рекурсивных функциях. Тезис Черча.
- •19. Понятие о труднорешаемых , np, p и np-полных задачах. Взаимоотношение классов p, np и np-полных задач.
10. Символы и определение формулы логики предикатов.
Как и при рассмотрении исчисления высказываний, приведем сначала символы, используемые в логике предикатов.
1.
Символами p,q,r
будем обозначать переменные высказывания,
принимающие два значения: 1
истина и 0
![]() ложь.
ложь.
2.
Символами x,y,z
будем обозначать так называемые
предметные переменные, т.е. этим символам
ставятся в соответствие имена некоторых
предметов; символами
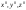 будем обозначать предметные константы,
т.е. конкретные значения предметных
переменных. Например, если символом
будем обозначать предметные константы,
т.е. конкретные значения предметных
переменных. Например, если символом
![]() мы обозначим предмет “стол”, то
возможными его значениями могут быть:
мы обозначим предмет “стол”, то
возможными его значениями могут быть:

“стол деревянный”, “стол металлический”
и т.д.
“стол деревянный”, “стол металлический”
и т.д.
3.
Большими буквами латинского алфавита
с предметными переменными в скобках,
т.е. P(x),Q(x)…,
будем обозначать одноместные предикаты
(их еще называют предикатными переменными
или переменными предикатами, если под
одним и тем же обозначением понимают
разные предикаты). Иначе говоря,
возможными значениями предикатных
переменных являются предикаты. Например,
в качестве P(x)
могут выступать различные предикаты:
“
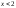 ”,
“
”,
“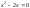 ”,
“
”,
“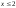 ”
и т.д.
”
и т.д.
 ,
,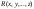
n-местные
предикатные переменные, т.е. переменные,
возможными значениями которых являются
n-местные
предикатные переменные, т.е. переменные,
возможными значениями которых являются
![]() -местные
предикаты. P0(x),
-местные
предикаты. P0(x),
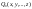
символы одноместных и многоместных
постоянных предикатов. Это такие
предикаты, за которыми закреплено
какое-то одно определенное свойство в
пределах рассматриваемой теории.
Например,
символы одноместных и многоместных
постоянных предикатов. Это такие
предикаты, за которыми закреплено
какое-то одно определенное свойство в
пределах рассматриваемой теории.
Например,
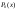
“x
четное число”
это предикат четности,
“x
четное число”
это предикат четности,
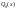
“x
рациональное число”, или
“x
рациональное число”, или
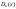
“x:y”
предикат делимости и т.д.
“x:y”
предикат делимости и т.д.
4.
Символы логических операций:

5.
Символы кванторных операций:
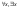
6.
Символы отношений:
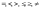
7. Вспомогательные символы: скобки, запятые.
Теперь дадим определение формуле логики предикатов.
1) каждое переменное высказывание является формулой.
2)
каждая n-местная
предикатная переменная
 или n-местный
постоянный предикат
или n-местный
постоянный предикат
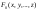 есть формула. Такие формулы, как и
формулы пункта 1, называются элементарными.
В них предметные переменные являются
свободными, не связанными кванторами.
есть формула. Такие формулы, как и
формулы пункта 1, называются элементарными.
В них предметные переменные являются
свободными, не связанными кванторами.
3)
если A
и B
формулы, причем такие, что одна и та же
предметная переменная
входит в обе формулы либо связно, либо
свободно, то слова
 ,
,
 и
и
 есть формулы.
есть формулы.
4)
если A
формула, то

тоже формула и характер предметной
(имя) переменной при переходе от формулы
A
к формуле
тоже формула и характер предметной
(имя) переменной при переходе от формулы
A
к формуле
 не меняется.
не меняется.
5)
если A(x)
формула, в которую предметная переменная
![]() входит свободно, то слова
входит свободно, то слова
 и
и
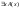 являются формулами, причем предметная
переменная входит в них связно.
являются формулами, причем предметная
переменная входит в них связно.
6. Всякие слова, отличные от тех, которые названы формулами в пунктах 1 – 5, не являются формулами.
Например,
если A(x)
и B(x,y)
одноместный и двухместный предикаты,
x,y
предметные переменные, а q.r
переменные высказывания, то слова q,
A(x),
B(x,y),
A(x) B(x,y),
B(x,y),
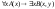 ,
,
 являются формулами.
являются формулами.
Примером
слова, не являющегося формулой, является
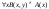 .
Здесь условие пункта 3 не выполняется,
так как в формулу
.
Здесь условие пункта 3 не выполняется,
так как в формулу
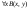 переменная
переменная
![]() входит
связно, а в формулу A(x)
свободно.
входит
связно, а в формулу A(x)
свободно.
