[Править]Определение

Вещественнозначная функция, определённая на некотором интервале (в общем случае на выпуклом подмножестве некоторого векторного пространства) выпукла, если для любых двух значений аргумента x, y и для любого числа выполняется неравенство Йенсена:

Если это неравенство является строгим для всех , функция называетсястрого выпуклой; если выполняется обратное неравенство, функция называетсявогнутой, или выпуклой вверх.

NB! Иногда выпуклая функция определяется как вогнутая и наоборот.

[Править]Свойства

• Функция f, выпуклая на интервале 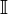, непрерывна на всём , дифференцируема на всём  за исключением не более чемсчётного множества точек и дважды дифференцируема почти везде.

• Непрерывная функция f выпукла на  тогда и только тогда, когда для всех точек  выполняется неравенство

• Непрерывно дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её графиклежит не ниже касательной, проведённой к этому графику в любой точке промежутка выпуклости.

• Дважды дифференцируемая функция одной переменной выпукла на интервале тогда и только тогда, когда её втораяпроизводная неотрицательна на этом интервале. Если вторая производная дважды дифференцируемой функции строго положительна, такая функция является строго выпуклой, однако обратное неверно (например, функция f(x) = x⁴ строго выпукла на [ − 1,1], но её вторая производная в точке x = 0 равна нулю).

• Если функции f, g выпуклы, то любая их линейная комбинация af + bg с положительными коэффициентами a, b также выпукла.

• Локальный минимум выпуклой функции является также глобальным минимумом (соответственно, для выпуклых вверх функций локальный максимум является глобальным максимумом).

• Любая стационарная точка выпуклой функции будет глобальным экстремумом.

• Для выпуклых функций выполняется неравенство Йенсена:

     где X — случайная величина со значениями в области определения функции f, E — математическое ожидание.

10

Точка перегиба

Определение

Точка перегиба функции  внутренняя точка x₀ области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x₀ является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.

[Править]Неофициальное

В этом случае точка (x₀;f(x₀)) является точкой перегиба графика функции, то есть график функции f в точке (x₀;f(x₀))«перегибается» через касательную к нему в этой точке: при x < x₀ касательная лежит под графиком f, а при x > x₀ — над графиком f (или наоборот)

[Править]Условия существования

Необходимое условие существования точки перегиба: если функция f(x), дважды дифференцируемая в некоторой окрестности точки x₀, имеет в x₀ точку перегиба, то .

Достаточное условие существования точки перегиба: если функция f(x) в некоторой окрестности точки x k раз непрерывно дифференцируема, причем k нечётно и , и  при , а , то функция f(x) имеет вx₀ точку перегиба.

Основы интегрального вычисления

1

Первообра́зной^[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция  является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных; таких как  или  … и т. д.; таким образомсемейство первообразных функции x² можно обозначить как F(x) = x³ / 3 + C, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная Gотличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например,  с f(0) = 0 не непрерывна при x = 0, но имеет первообразную  с F(0) = 0.

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции(такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.

2

Неопределённый интегра́л для функции  — это совокупность всех первообразных данной функции.

Если функция  определена и непрерывна на промежутке  и  — её первообразная, то есть при , то

 ,

где С — произвольная постоянная.

Если , то и , где u = φ(x) — произвольная функция, имеющая непрерывную производную

3

Таблица основных неопределённых интегралов

 

 

Слева в каждом равенстве стоит произвольная (но определённая) первообразная функция для соответствующей подынтегральной функции, справа же — одна определённая первообразная, к которой ещё прибавляется константа  такая, чтобы выполнялось равенство между этими функциями.

Первообразные функции в этих формулах определены и непрерывны на тех интервалах, на которых определены и непрерывны соответствующие подынтегральные функции. Эта закономерность не случайна: как отмечено выше, всякая непрерывная на интервале функция имеет на нем непрерывную первообразную.

4

Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Данное выше определение интеграла при всей его кажущейся общности в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x₀ < x₁ < x₂ < x_n = b Тогда говорят, что произведено разбиение R отрезка [a;b] Далее выберем произв. точку , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм Θ_R при , если он существует независимо от разбиения R и выбора точек ξ_i, т.е.  (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

• 

• a – нижний предел.

• b – верхний предел.

• f(x) – подынтегральная функция.

• λ_R - длина частичного отрезка.

• σ_R – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R.

• λ_R - максимальная длина част. отрезка.

Определение интеграла на языке , δ:(по "Коши") Число I – называется определённым интегралом от f(x) на [ a ; b ], если для любого ε>0 существует δ=δ(ε)>0: для любого разбиения R отрезка [ a ; b ]: λ_R < δ, выполняется неравенство: |I- σ_R | = |∑^n-1_i=0f(ξi) Δxi - I| < ε при любом ξi є [ xi ; xi+1] Тогда I = ∫_a^bf(x)dx