Производная
1
Произво́дная — функция, являющаяся результатом применения той или иной операции дифференцирования к исходной функции. Физический смысл производной — скорость изменения величины или процесса. Разновидности:
-
Производная функции
-
Производная (обобщения)
-
Частная производная
-
Производная по направлению
Произво́дное множество множества A — совокупность всех предельных точек этого множества.
Тангенс угла наклона касательной прямой
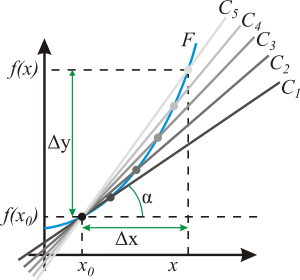
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точкиx0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.
Основная статья: Касательная прямая
Если
функция 
имеет
конечную производную в точкеx0, то
в окрестности U(x0) её
можно приблизить линейной
функцией
Функция fl называется
касательной к f в
точке x0. Число 
является
угловым коэффициентом
или тангенсом угла наклона касательной
прямой.
2
Дифференци́руемая фу́нкция — это функция, имеющая дифференциал. Дифференцируемая функция может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат (на данном отрезке).
Функция
называется дифференцируемой в точке x0 своей области определения M, если существует такая линейная функция
,
что для любой точки x области M верно
,
то есть, раскрывая символ «o» малое, если
.
Множество всех функций, определённых и дифференцируемых во всех точках области M является кольцом
4
|
|
|
|||
|
y=f(x) |
y=f’(x) |
y=f(x) |
y=f’(x) |
|
|
y = c (c – const) |
y’ = 0 |
y = ln x |
y’ = 1/x |
|
|
y = x |
y’ = 1 |
y = sin x |
y’ = cos x |
|
|
y = x2 |
y’ = 2x |
y = cos x |
y’ = – sin x |
|
|
y = xn (n принадлежит N) |
y’ = nxn–1 |
y = tg x |
y’ = 1/(cos2x) |
|
|
y = x–n (n принадлежит N) |
y’ = – nxn–1 |
y = ctg x |
y’ = – 1/(sin2x) |
|
|
y = xα (α > 0) |
y’ = αxα–1 |
y = arcsin x |
y’ = 1/√1 – x2 |
|
|
y = x–α (α > 0) |
y’ = –αx–α–1 |
y = arccos x |
y’ = – 1/√1 – x2 |
|
|
y = ax (a > 0, a ≠ 1) |
y’ = axln a |
y = arctg x |
y’ = 1/( 1 + x2 ) |
|
|
y = ex |
y’ = ex |
y = arcctg x |
y’ = – 1/( 1 + x2 ) |
|
|
y = logax (a > 0, a ≠ 1) |
y’ = 1/(x lna) |
|
|
|
5
1. Техника вычисления производных
1.1. Правила вычисления производных.
I. Если существует f
0
(p) и k 2 R, то существует и (k f)
0
(p), и при этом (k f)
0
(p) =
k f
0
(p).
II. Если существуют f
0
(p) и g
0
(p), то существует и (f+g)
0
(p), и при этом (f+g)
0
(p) =
f
0
(p) + g
0
(p).
III. Если существуют f
0
(p) и g
0
(p), то существует и (f g)
0
(p), и при этом
(f g)
0
(p) = f
0
(p)g(p) + f(p)g
0
(p):
IV. Если существуют f
0
(p) и g
0
(p) и g(p) = 0 6 , то существует и
f
g
0
(p), и при этом
f
g
0
(p) =
f
0
(p)g(p) f(p)g
0
(p)
[g(p)]
2
:
V. Если существуют f
0
(p) и g
0
(f(p)), то существует и (g
f)
0
(p), и при этом
(g
f)
0
(p) = g
0
(f(p)) f
0
(p):
VI. Пусть существует окрестность точки p, в которой функция f непрерывна и
обратима. Если функция f обладает производным числом f
0
(p) в точке p и
f
0
(p) = 0 6 , то обратная к f функция f
1
обладает производным числом в точке
q = f(p), и при этом
f
1
0
(q) =
1
f
0
(p)
6
Производная сложной функции
Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x0, а функция g имеет производную в точке y0 = f(x0), то сложная функция h(x) = g(f(x)) также имеет производную в точке x0.
Пусть
даны функции, определённые в окрестностях
на числовой прямой, 
где y0 = f(x0), и 
Пусть
также эти функции дифференцируемы: 
Тогда
их композиция также дифференцируема: 
и
её производная имеет вид:
7
-
(Критерий монотонности функции, имеющей производную на интервале) Пусть функция
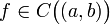непрерывна
на (a,b), и
имеет в каждой точке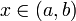 
производную f'(x). Тогда
f возрастает
на (a,b) тогда
и только тогда, когда 
f убывает
на (a,b) тогда
и только тогда, когда 
-
(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция
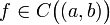непрерывна
на (a,b), и
имеет в каждой точке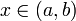 
производную f'(x). Тогда
если 
то f строго
возрастает на (a,b);
если 
то f строго
убывает на (a,b).
Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место
-
(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть
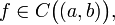и
всюду на интервале определена
производная f'(x). Тогда f строго
возрастает на интервале (a,b) тогда
и только тогда, когда выполнены следующие
два условия:
Аналогично, f строго убывает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:
"Условия монотонности функции (Критерий монотонности функции, имеющей производную на интервале): Пусть функция непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда - f НЕ УБЫВАЕТ на (a,b) тогда и только тогда, когда ...далее по тексту f НЕ ВОЗРАСТАЕТ на (a,b) тогда и только тогда, когда ...далее по тексту"
8
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданноммножестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
9
Выпуклая функция — функция, у которой надграфик является выпуклым множеством.