2. Приклади типових завдань, що виносяться на іспит.

Студент по закінченню курсу має не лише володіти теоретичними засадами дисципліни, але й вміти використовувати їх для розв’язання практичних завдань. Приклади практичних завдань, що виносяться на іспит, приведено нижче.

1 Семестр

1.Обчислити визначник:

1) , 2).

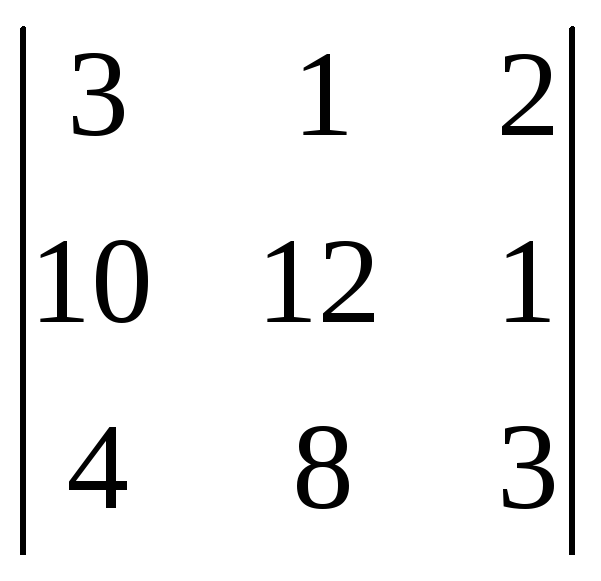2.Розв’язати систему рівнянь за формулами Крамера:

.

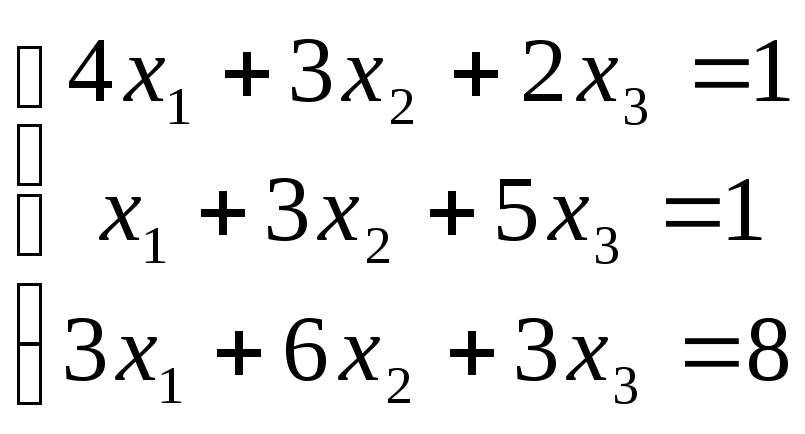3.Знайти матрицю :

1) С=3А-2В, 2), якщо

.

4. Розв”язати систему рівнянь за допомогою оберненої матриці:

1)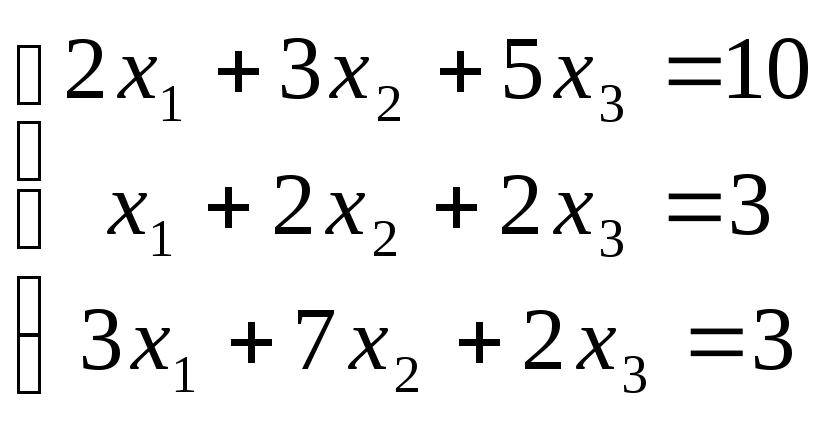, 2)

5. Обчислити ранг матриці :

6. Дослідити систему рівнянь на сумісність:

.

7. У разі існування оберненої матриці побудувати її для заданої. Наприклад,

.

8. Розв»язати систему рівнянь методом Гаусса або Жордана-Гаусса. Наприклад,

.

9. Довести , що вектори утворюють базис та розкласти вектор х за базисом. Наприклад,

10. Встановити кількість ЛНЗ векторів для даної системи векторів

11. Знайти власні числа та власні вектори матриці. Наприклад,

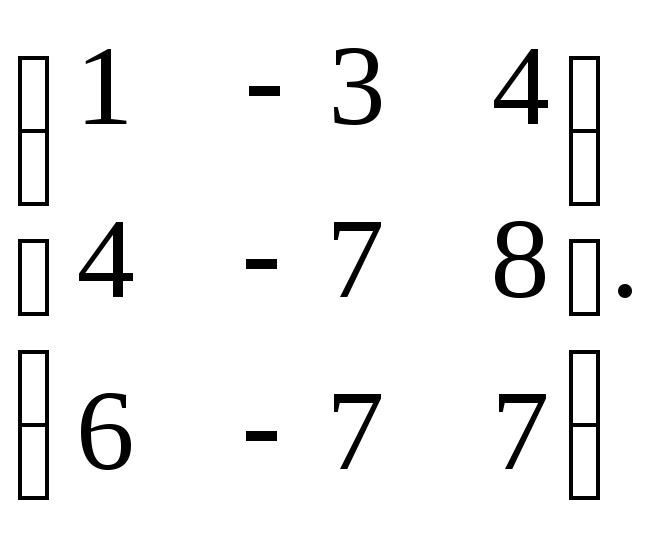
12. Встановити визначеність квадратичної форми:

13. Знайти матрицю лінійного перетворення від базису

до базису

14. Паралелограм побудовано на векторах де

Знайти:

1. Довжину діагоналей паралелограма ;

2. Кут між діагоналями;

3. Площу паралелограма ;

4. Проекцію

15. Дано трикутник АВС, А(3,2), В(-1,0), С(2,-3). Знайти рівняння:

a) сторони АВ ;

b) медіани АЕ ;

c) бісектриси СР ;

d) висоти ВК ;

e) середньої лінії МН що паралельна ВС.

Обчислити довжини:

a) сторони АВ; b) медіани АЕ ; c) бісектриси СР ; d) висоти ВК .

Обчислити:

a) Площу трикутника АВС;

b) Кут між медіаною АЕ та бісектрисою СР.

16. Дано ОАВС – піраміда. О(5,-9,-1), А(5,1,2) ,В(-4,-3,6),С(-9,6,7).

Знайти рівняння:

a) грані ОАВ;

b) ребра АО;

c) висоти ОК;

d) площини , що проходить через ребро АО перпендікулярно до основи.

Обчислити:

a) площу основи АВС;

b) об»єм піраміди;

c) довжину висоти;

d) кут між ребрами АО та ОВ;

e) віддаль від ребра АО до сторони основи ВС.

17. Задано рівняння кола Знайти:

1. координати центра та довжину радіуса;

2. найкоротшу віддаль від точки М(3,9) до кола;

3. рівняння дотичної із точки К(-5,8) до кола.

18. Знайти ексцентриситет та координати фокусів:

a) еліпса

2. гіперболи

19. Знайти рівняння директриси та координати фокуса параболи

20. Знайти віддаль від директриси параболи

до фокусів еліпса

21. Знайти кут між асимптотами гіперболи

22. Знайти віддаль від асимптот гіперболи

до фокусів еліпса

23. Знайти область визначення функції

.

24. Знайти множину значень функції .

25. Встановити характер точек розриву функцій

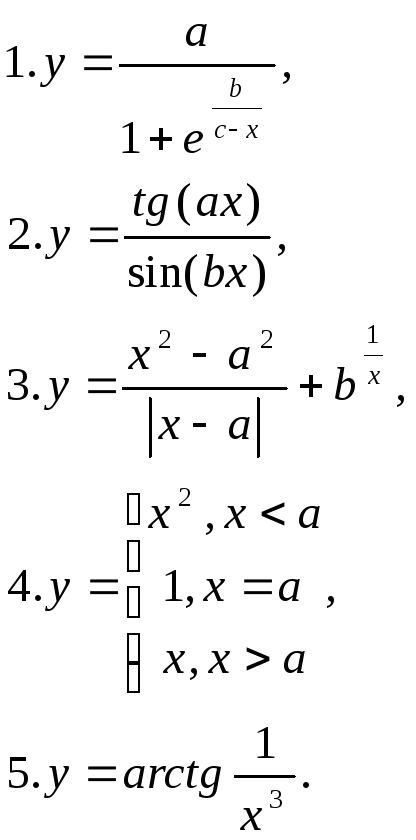
26. Знайти похідну функції:

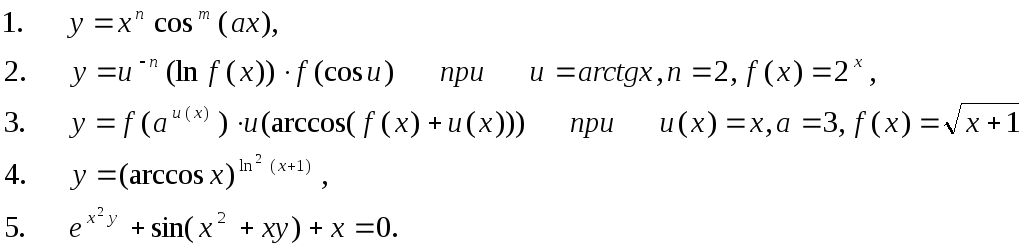
27. Обчислити границі:

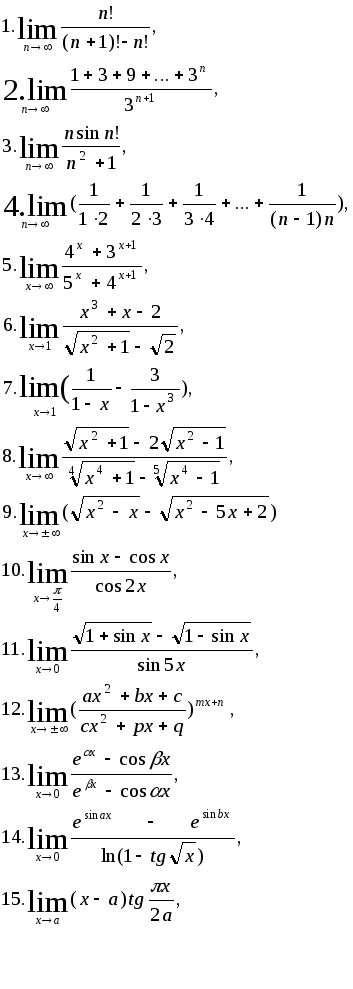
28. Знайти диференціал функції:

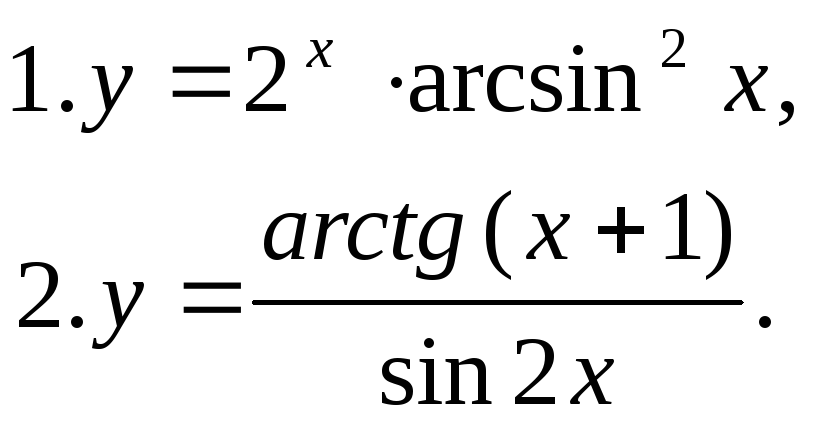
29. Знайти похідну другого порядку:

30. Знайти рівняння дотичної та нормалі до графіка функції

у точках перетину графіка із віссю Ох.

31. Знайти точку, в якій дотична до графіку функції

паралельна хорді, що проходить через точки : А(0;1), В(1;7).

32. Знайти екстремуми та інтервали монотонності функції:

33. Знайти точки перегину та інтервали напряму опуклості функції:

34. Знайти асимптоти функції

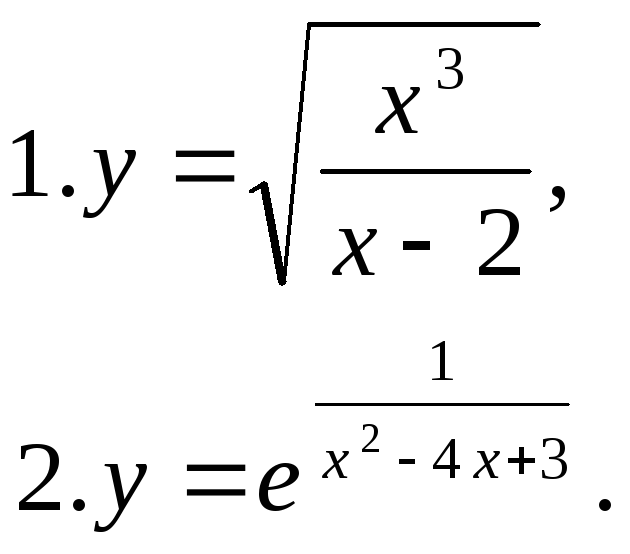
35. Знайти найбільше та найменше значення функції

на проміжку [-1;2].