2.4.2 Вероятностный подход к описанию погрешностей

В теории измерений для описания погрешности измерений используют интегральные и дифференциальные законы (функции) распределения. Под интегральной функцией распределения случайной погрешности понимают вероятность того, что случайная погрешность в -том опыте окажется меньше некоторого текущего значения , т.е.. Данное определение можно пояснить с помощью рис 1.3.

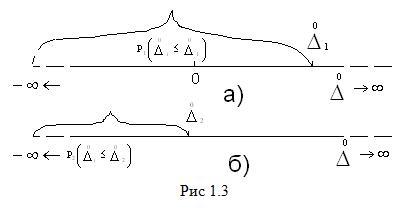
На рисунке показана числовая ось возможных значений погрешностей (в общем случае они могут принимать любые значения от =-∞ до =+∞). Отметим на этой оси текущее значение . Тогда, если это текущее значение  расположено в правой части числовой оси (рис. 1.3,а), то в интервале от =-∞ до = попадает большее число случайных погрешностей, характеризуемое вероятность , чем в том случае, если текущее значение  расположено левее (рис. 1.3, б) и характеризуемое вероятностью , т.е. . Так как вероятностью события называется численная мера степени объективной возможности этого события и достоверным событием называется событие, которое в результате опыта непременно должно пройти, а невозможным – которое произойти не может, то вероятность любого события заключена между нулём и единицей. В нашем случае достоверным событием является появление случайной погрешности £+∞, а невозможным событием появления случайной погрешности £-∞. Следовательно (+∞)=1, а (-∞)=0. Поэтому график интегральной функции распределения - монотонно возрастающая функция, имеющая вид рис 1.4.

Прикладной характер имеет дифференциальная функция распределения, называемая также плотностью распределения вероятностей и обозначаемая (). По определению плотностью распределения называется функция ()=(). Один из возможных графиков этой функции показан на рис.1.5.

Т.к. (+∞)=1, то =(+∞)=1, т.е. площадь, заключенная между кривой дифференциального закона распределения и осью абсцисс, равна единице.

При проведении измерения вероятность попадания случайной погрешности  в интервал (,) можно оценить по формулам

(≤≤)=  ()-() или(≤≤)=.

Таким образом, вероятность попадания случайной погрешности в заданный интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границе этого интервала. Значения абсцисс и  называются квантилями распределения, а интервал между ними называют интерквантильным интервалом с указанием соответствующей вероятности (≤≤). Форма кривой распределения позволяет судить о том, какие интервалы значений случайных погрешностей более или менее вероятны.

Результат измерения, содержащий случайную погрешность, также является случайной величиной и может характеризоваться интегральной функцией распределения – вероятность того, что результат измерения в -м опыте окажется меньше некоторого текущего значения  и дифференциальной функцией распределения.

Погрешность измерения удобно выражать в виде числа. Из теории вероятностей известно, что закон распределения можно характеризовать числовыми характеристиками – моментами (неслучайные числа), которые используются для количественной оценки погрешности. Основными числовыми характеристиками законов распределения являются математическое ожидание (момент 1-го порядка) и дисперсия (момент 2-го порядка), которые определяются выражениями

[]=;

[]=.

Здесь  и  – символы математического ожидания и дисперсии; - общая погрешность результата измерения, которая, как уже говорилось, включает систематическую и случайную составляющую . Математическое ожидание погрешности измерений есть неслучайная величина, относительно которой рассеиваются другие значения погрешностей при повторных измерениях, т.е. оно характеризует систематическую составляющую погрешности измерения []= (cм рис. 1.6).

Рис. 1.6

Тогда случайная погрешность может быть записана в виде =-=-[] и, по определению, она является центрированной случайной величиной. Дисперсия погрешности [] характеризует степень рассеивания (разброса) отдельных значений погрешности относительно математического ожидания. Т.к. рассеивание происходит за счет случайной составляющей погрешности, то []=[]. Чем меньше дисперсия, тем меньше разброс, тем точнее выполнено измерение. Следовательно, дисперсия может служить характеристикой точности проведенных измерений. Т.к. она выражается в единицах погрешности в квадрате, то используют на практике среднее квадратическое отклонение (погрешность) – СКО(СКП), которое равно положительному корню из дисперсии []=. Для более подробного описания распределения используют моменты более высоких порядков.