Блок-схема построения кубического сплайна
х0
xi
xi-1
х2
xn
х1
xn-1
Д
ля
переменных х
[xi-1,xi]
(i=1,2,…n)
о
в
а
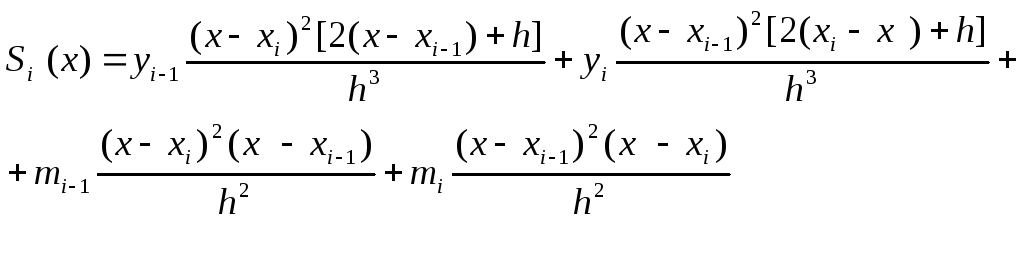
- шаг. mi
определятся рекуррентным соотношением:
f’(a)=m0=A; f’(b)=mn=B; mi=Li M i+1+Mi (i=n-1,n-2,…0), где L0=0; M0=m0;
L
;
Mi=Li(Mi-1-bi)
(i=1,2…,n-1) ; bi=
A и В –заданы А= f’(a); B=f’(b)
m(0) =1;
m(n) =0;
l(0) =0;
h=(b-a)/n
bi=
;
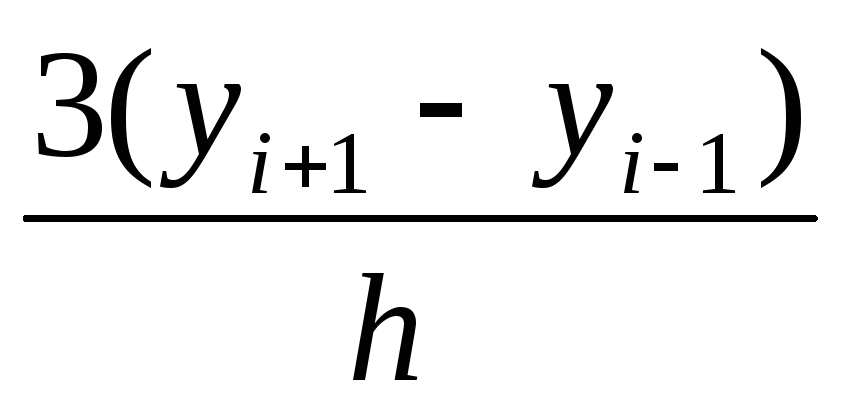li=
mi =
li (mi-1
– bi)
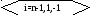
mi =limi+1
+ mi
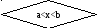
i=yсл.часть[(x-a)/h]+1;
x0=a+(i-1)h
,x1=x0+h
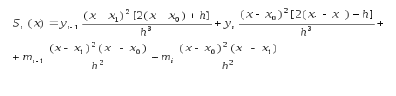
ЛЕКЦИЯ 11
Численное дифференцирование
1.Производная функция f(x) в точке х0 определена, как
y’(х0)=f’(х0)=
,
(1)
Пусть
, здесь
-начальное
приращение аргумента
a>1- некоторое число. n=0,1,2….
Тогда
Т.о.
(2)
Точность приближения (2) можно оценить формулой Тейлора (если f(x) непрерывные функции, имеющие 1-ую и 2-ю производные)
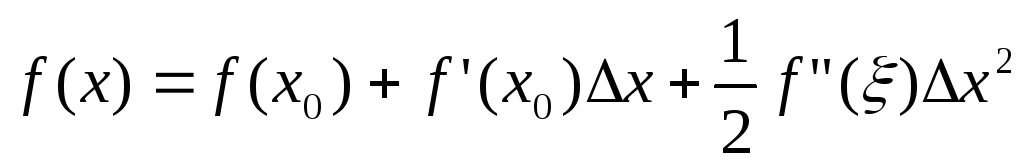
Тогда
M=
Окончательно имеем:
,где L=
т.к
;
Для достижения заданной точности
приближения производной можно использовать
неравенство:
<
(3)
Пример:
Вычислить производную ф-ии y=sinx
в точке
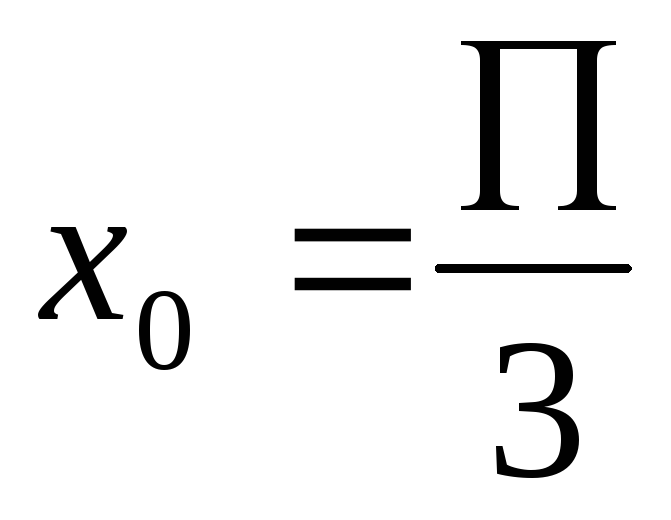с точностью
=10-3
. (П/3=1.047198)
Решение:
Положим
Тогда
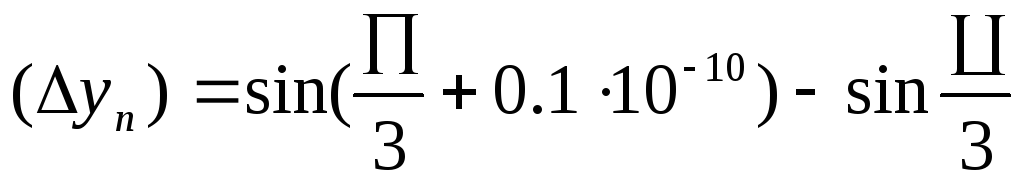
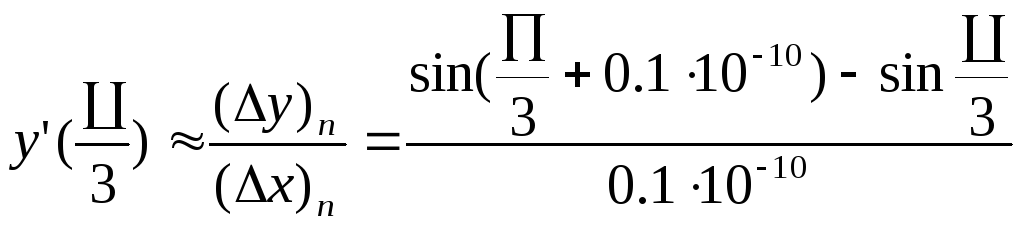(n=0,1,2.….)
Получаем:
=0.45590189;
=0.49566158;
=0.49956690;
=0.49995670;
=0.000389793<
;
y’(П/3)=0,5; т.о. достаточно взять 3-е приближение.
2.Конечно-разностные аппроксимации производных.
Пусть отрезок [а,b] разбит
на n (n
2)
равных частей.
Производные можно записывать с помощью конечных разностей:
а) разностей вперед:
;
( i=0,1,….,n-1)
(1)
в) разностей назад (левые разности):
;
(2)
c) центральных разностей:
;
Приближенное значение производной второго порядка в точке хi :
,
;
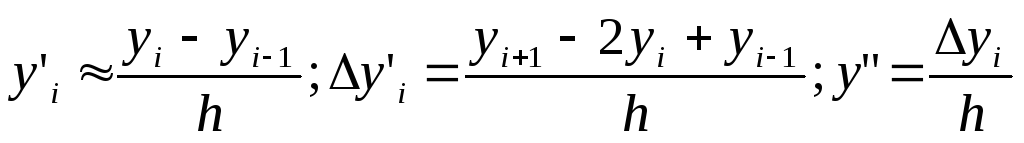
Т.о
i=1,2,…..n-1
(3)
Погрешность аппроксимации (3) имеет
порядок 0 (
).
3. Использования интерполяционных многочленов Лагранжа для формул численного дифференцирования.
Функция у=f(x) на отрезке [a,b] разбитых на n равных интервалов, принимает значение в точках {xi} (i=0,1,2….k)
yi=f(xi) ; b=xn ; h=xi-xi-1=const.
Построим интерполяционный многочлен Лагранжа Lm(x) степень M:
Lm(x)=f(x
k)=y
k
(k=i,i+1,….,i+m) i+m
n.
Многочлен Lm(x) интерполирует функцию f(x) на отрезке [xi,xi+m].
Дифференцируя Lm(x), получаем значение производных в точках {xk} (k=i,i+1,…,i+m).
(Можно получить значения и в точках ,отличных от узлов.)
Если m=1 , то L1(x)-линейная функция , график которой проходит через точки (хi,yi) и (хi+1,yi+1). Тогда
L1(x)=
; L1’(x)=
Если m=2, то график L2(x) – парабола, проходящая через точки (хi,yi) , (хi+1,yi+1), (хi+2,yi+2).
L2(x)=
L2’(x)=
(1)
L2”(x)=
(2)
Подставляя в (1) и (2) значения х, равные хi,xi+1,xi+2:
Получим приближения производных f’(x) и f”(x) в этоих точках :
учитывая, что
;
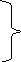
(3)
(4)
Если функция f(x) имеет непрерывную производную до 3-го порядка включительно ,то
;
f(x) = L2(x)+ R2(x), (5)
где R2(x)- остаточный член интерполяционной формулы.
R2(x)=
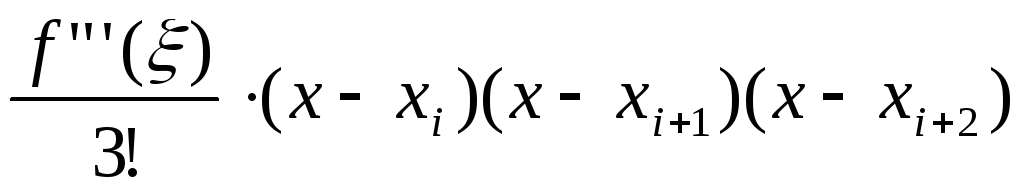
Дифференцируя (5) ,получим
f’(x) = L’2(x)+ R’2(x) (6)
f”(x) = L”2(x)+ R”2(x) (7)
Здесь,
R’2(x)=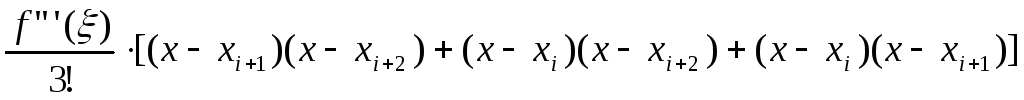
;
(8)
Т.к. f”’(
)=const
–дифференцируем по х.
R”2(x)=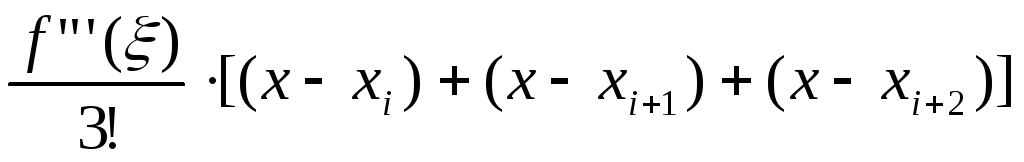
;
В точках хi,xi+1,xi+2 (т.е. в узлах) получаем (подставляя значения хi и т.д. в (8)-(9) и учитывая хi-xi+1=-h) :
R’2(xi)=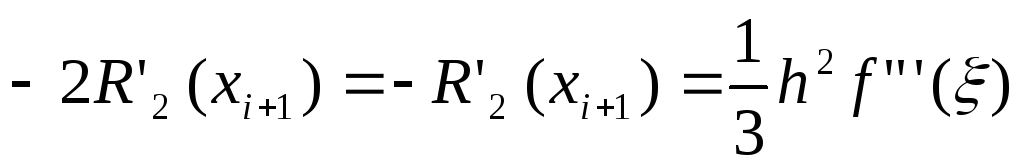
(10)
R”2(xi)=
,
,
=
(11)
Т.о. равенства (10) показывают, что погрешность аппроксимации первой производной f’(x) с помощью формулы (3) имеет один и тот же порядок 0(h2). (во всех трех точках.)
На отрезке [a,b]
в точках хi
(i=0,1,2…,n)
при n
2
рекомендуется применять следующие
формулы:
i=0;
(i=1,2,…,n-1);
(12)
i=n;
Погрешность аппроксимации второй производной имеет различный порядок в различных точках .(равенство(11)).Поэтому рекомендуется использовать многочлен Лагранжа третьей степени L3(x), имеющей 4 точки (узла) интерполяции. При этом погрешность во всех точках имеет один порядок h2.
Рекомендуется формулы:
i=0;
( i=1,2,….,n-1);
i=n;
Пример:
Значение функции y=sin x заданы таблицей
-
x
0
П/6
П/3
sinx
0
0.5
0.866
Найти значения
и
и оценить погрешности вычислений.
Решение:
По формулам (3) или (12) получаем:
;
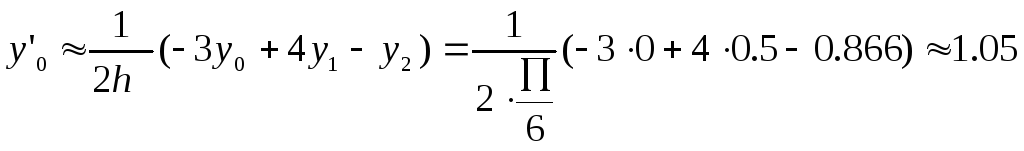По формуле (1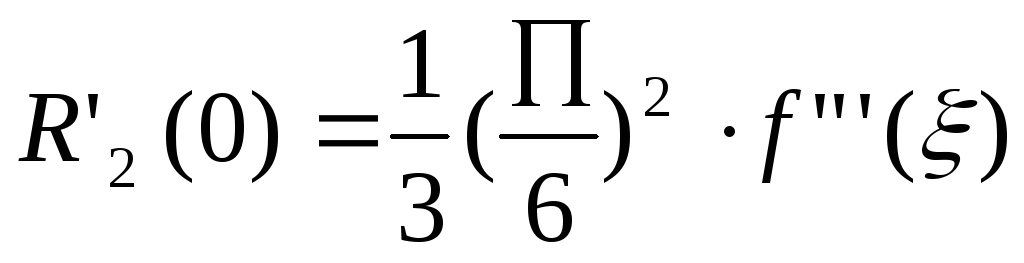0):
0<
<
Т.к f(x)=sin x, то f”’(x)=-cos x.
.
Т.о. y’0
1.05
0.09
По формуле (4)
По формуле (11):
получаем
Т.о. y’0
-0.489
0.52.
Точность явно низкая.
y”0=sin0=0
Следовало бы уменьшить шаг и увеличить число шагов. Затем использовать полином Лагранжа 4-ой степени и формулы (13).