Геометрический смысл дифференциала.

Итак, приращение функции можно представить в виде

Первое слагаемое пропорционально , т.е. оно - линейная однородная функция от . Второе, является бесконечно малой высшего порядка малости , т.е. оно стремится к нулю быстрее, чем первое. В связи с этим первое слагаемое называется главным членом приращения (при ). Это слагаемое называют дифференциалом функции и обозначают символом . Итак, по определению

На рисунке - касательная к кривой в точке , , приращение функции соответствует приращению аргумента . При этом

Вообще говоря . Равенство выполняется только для линейной функции. В этом случае дифференциал и приращение независимой переменной равны между собой . Поэтому дифференциал произвольной функции записывают обычно так

Основные теоремы о дифференциалах, дифференциал

сложной функции

1)

2)

3)

4)

5)

6) Форма дифференциала инвариантна (неизменна).

Дифференциал функции равен произведению производной на дифференциал аргумента независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Например, дифференциал сложной функции.

Применение дифференциалов к приближенным

вычислениям

Итак

Отсюда следует, что дифференциал функции при достаточно малом может служить хорошим приближением приращения функции. В этом смысле пишут приближенное равенство

где .

Например, вычислить значение . Имеем , , .

Далее . Или . Окончательно

Дифференциалы высших порядков.

1) Если , то .

2) Если , то

Например. Дано уравнение эллипса . Найдем первую производную

Вторая производная. Имеем . Отсюда

Теорема ( Ферма).

Если функция имеет производную в точке и достигает в этой точке локального экстремума, то .

Доказательство.

По определению производной имеем

Так как у нас (мы считаем, для определенности, что имеет место локальный максимум) , то для достаточно малых

Откуда в пределе, при , получим, что .

Если же , то

Поэтому, переходя к пределу при в этом неравенстве, поучим . Отсюда и вытекает .

Теорема 11 (Ролля).

Если функция непрерывна на , дифференцируема на и , то существует точка , такая, что .

Доказательство.

Если постоянна на , то для всех производная .

Б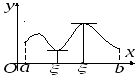удем считать, что не постоянна на . Так как непрерывна на , то существует точка , в которой достигает максимума на , и существует точка , в которой достигает минимума на . Обе точки не могут быть концевыми точками отрезка , потому что иначе

и была бы постоянной на . Следовательно, одна из точек принадлежит интервалу . Обозначим ее через . В ней достигается локальный экстремум. Кроме того, существует, потому что по условию существует для всех . Поэтому по теореме Ферма .

Теорема 12 ( Коши).

Если функции и непрерывны на и дифференцируемы на , и в , то существует точка такая, что

Доказательство. Отметим, что , так как в противном случае, по теореме Ролля, нашлась бы точка такая, что , чего быть не может по условию теоремы. Составим вспомогательную функцию

В силу условия теоремы эта функция непрерывна на , дифференцируема на и , . Применяя теорему Ролля, получим , что существует точка , в которой . Но

Поэтому, подставляя вместо точку , получим утверждение теоремы.