Математический анализ.
Оглавление.
1. Действительные числа.
2. Функция, понятие функции.
3. Предел числовой последовательности.
4. Предел функции.
5. Признаки существования пределов.
6. Бесконечно большие и бесконечно малые функции.
7. Замечательные пределы.
8. Непрерывные функции. Определение непрерывности.
9. Производная функции.
10. Основные правила дифференцирования.
11. Производные элементарных функций.
12. Геометрический смысл производной, уравнение касательной и нормали к кривой.
13. Дифференциал функции.
14. Применение дифференциального исчисления к исследованию функций. Локальный экстремум функции.
1. Действительные числа.
Простейшим
множеством чисел является множество
натуральных чисел
-
,
которые вместе с отрицательными числами
и числом
образуют множество целых чисел
.
Числа
целые и дробные, как положительные, так
и отрицательные составляют множество
рациональных чисел. Каждое рациональное
число может быть представлено в виде
дроби
,
где
и
- целые числа. Рациональные числа
представляются в виде конечных и
бесконечных периодических дробей. Все
остальные числа называются иррациональными
и представляются в виде бесконечных,
непериодических дробей.
Свойства действительных чисел.
1. Между двумя действительными числами всегда находится рациональное и иррациональное.
2. Любое иррациональное число можно с любой степенью точности заменить рациональным.
Совокупность всех рациональных и иррациональных чисел образует множество действительных (вещественных) чисел.
Ч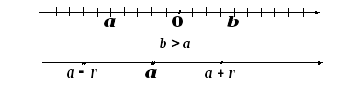
исловая
ось - это бесконечная прямая, на которой
выбраны:
1).
Некоторая точка
,
называемая началом отсчета.
2). Положительное направление, которое обозначается стрелкой.
3). Масштаб.
Действительные числа изображаются точками на числовой оси, и каждой точке числовой оси соответствует число.
Множество
чисел, удовлетворяющих условию
,
называется интервалом и обозначается
или
.
Множество
чисел, удовлетворяющих условию
,
называется отрезком и обозначается
.
Окрестностью
точки на числовой оси называется интервал
с центром в этой точке,
- радиус интервала.
Абсолютная величина действительного числа.
Абсолютная
величина или модуль числа
обозначается
и определяется следующим образом.
1. Модуль суммы конечного числа слагаемых не больше суммы модулей.
2. Модуль разности не меньше разности модулей
3. Модуль произведения равен произведению модулей
4. Модуль частного равен частному модулей
2. Функция, понятие функции
Рассмотрим
множество
элементов
и множество
элементов
.
Если каждому элементу
по определенному правилу
поставлен в соответствие единственный
элемент
,
то говорят, что на множестве
задана функция
со значениями во множестве
.
Элементы
называются значениями аргумента, а
элементы
- значениями функции. Множество
называется областью определения функции,
множество всех значений функции -
областью значений этой функции.
Например.
Функцию,
заданную на множестве
со значениями во множестве
,
называют отображением множества
во множество
.
Функцию
называют также оператором.
К традиционным, основным способам задания функции относятся: аналитический (с помощью одной или нескольких формул); графический (с помощью графиков); табличный, программа на ЭВМ.
Функция, заданная формулой
правая
часть которой не содержит
,
называется явной.
Функция
,
определяемая уравнением
называется функцией, заданной неявно, или неявной функцией.
Например.
