Матрицы
Оглавление.
1. Определение матриц.
2. Квадратные матрицы.
3. Действия с матрицами
4. Ранг матрицы.
5. Обратная матрица.
6. Системы линейных уравнений.
6.А. Метод Гаусса.
6.б. Формулы Крамера.
6.в. Матричный метод.
7. Системы линейных уравнений общего вида.
1. Определение матриц
Прямоугольная
таблица,
содержащая
строк и
столбцов, называется матрицей размера
.
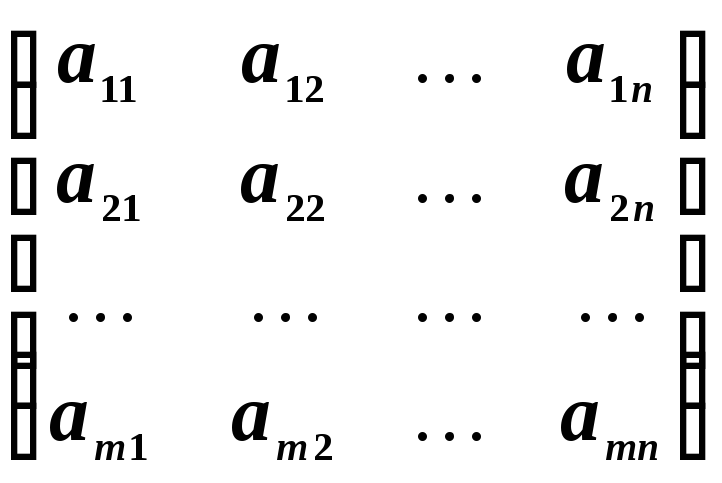
Числа
называются элементами матрицы. Каждый
элемент матрицы снабжен двумя индексами:
первый индекс указывает номер строки,
второй — номер столбца, в котором
расположен этот элемент.
Матрицы
обозначают буквами
,
,
и т. д. Например,
или
сокращенно в виде
.
Две
матрицы
и
считаются равными, если равно число их
строк и число столбцов и если равны
элементы, стоящие на соответствующих
местах этих матриц равны, то есть
,
если
.
Часто
приходится рассматривать матрицу,
столбцами которой являются строки
матрицы
.
Эта матрица называется транспонированной
к
и обозначается через
.
Пусть
дана матрица
.
Переставим строки со столбцами. Получим
матрицу
,
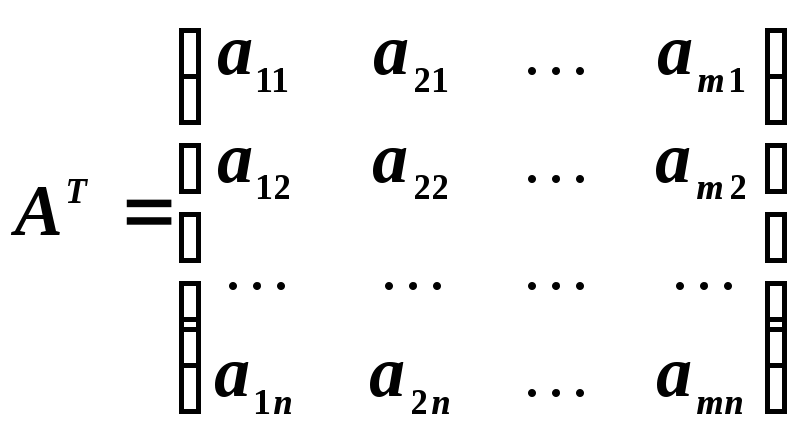которая
будет транспонированной по отношению
к матрице
.
2. Квадратные матрицы
Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число ее строк, равное числу столбцов, — порядком квадратной матрицы.
Множество
всех элементов квадратной матрицы,
которые лежат на отрезке, соединяющем
ее левый верхний угол с правым нижним,
т. е. совокупность элементов
называется главной диагональю, а
множество всех элементов, которые лежат
на отрезке, соединяющем ее правый верхний
угол с левым нижним, - побочной диагональю.
Квадратная матрица называется треугольной, если ее элементы, которые находятся над главной диагональю или под главной диагональю, равны нулю, т. е. матрицы вида
,
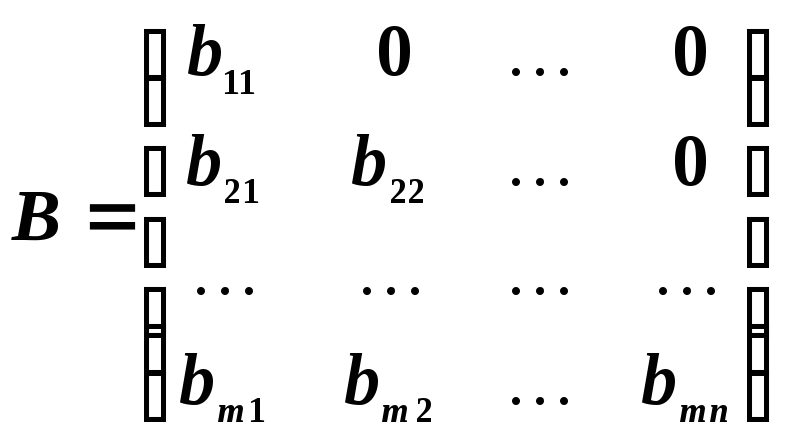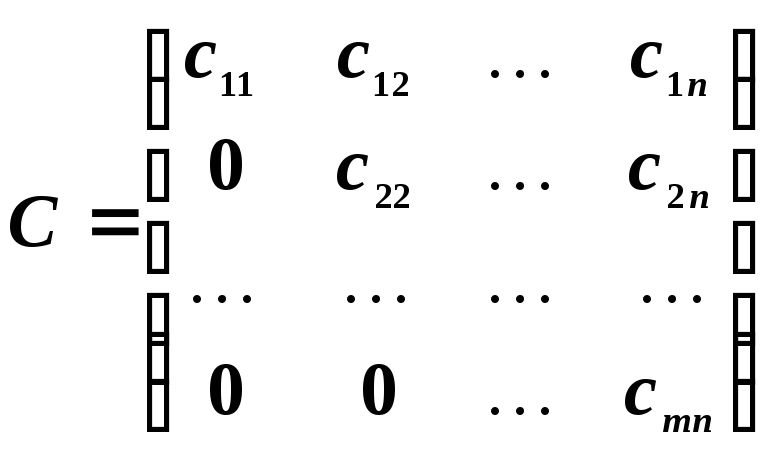
являются
треугольными. Матрица
называется треугольной снизу, а матрица
— треугольной сверху.
Квадратная
матрица называется диагональной, если
ее элементы, которые находятся вне ее
главной диагонали, равны
.
.
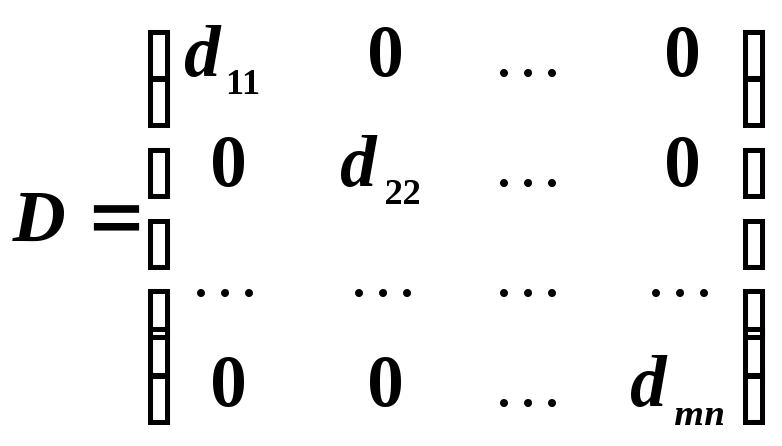3. Действия с матрицами Умножение матрицы на число и сложение матриц
По
определению, чтобы умножить матрицу на
число
,
нужно каждый элемент матрицы умножить
на это число.
Пример 1. Умножить матрицу на число
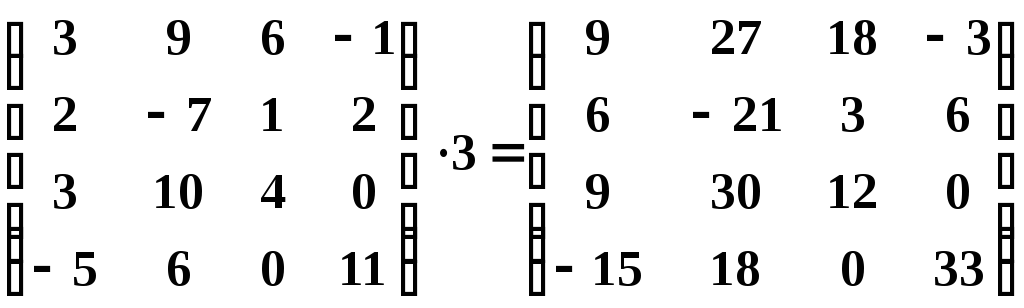
Складывать
можно только матрицы с одинаковым числом
строк и столбцов. Суммой матриц
и
называется матрица
,
элементы которой
равны суммам соответствующих элементов
матриц
и
:
.
Пример 2. Сумма двух матриц
.
Матрица,
все элементы которой равны нулю,
называется нулевой и обозначается через
.
Для любой матрицы
имеем
,
.
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1)
,
2)
,
3)
,
4)
,
5)
.
где
,
,
- матрицы,
,
- числа.
Произведение матриц
Произведение
матрицы
на матрицу
определено только в том случае, когда
число столбцов матрицы
равно числу строк матрицы
.
В результате умножения получим матрицу
,
у которой столько же строк, как у матрицы
,
и столько же столбцов, как у матрицы
.
По
определению элемент
матрицы
равен сумме парных произведений элементов
строки матрицы
,
на соответствующие элементы
столбца матрицы
.
Пример 3. Найти произведение матриц
и
.
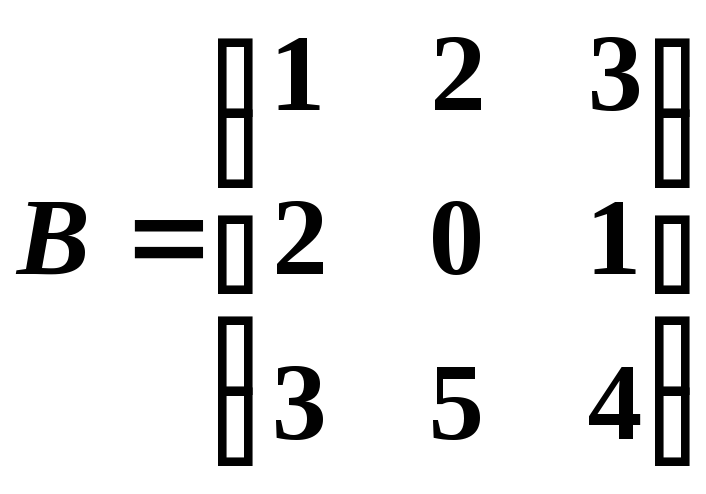Решение.
Имеем: матрица
размера
,
матрица
размера
,
тогда произведение
существует и элементы матрицы
равны
, 
, 
,
, 
.
,
а произведение
не существует.
Пример 4. Найти произведение матриц
,
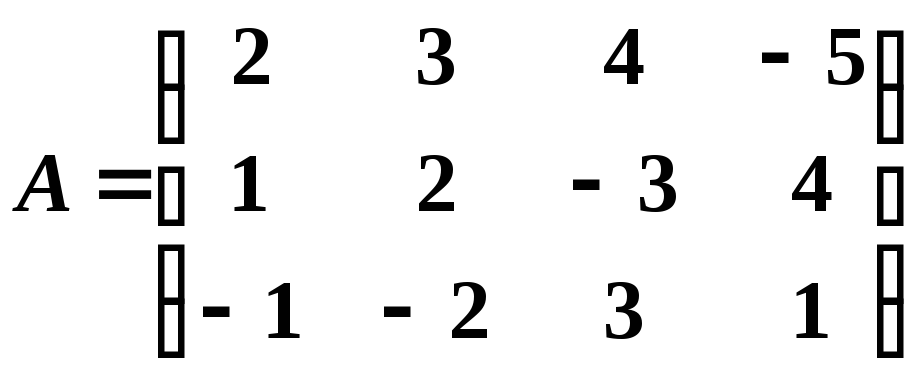Очевидно,
что произведение матриц не обладает
перестановочным свойством, т.е.
некоммутативно. Если все-таки выполняется
равенство
,
то матрицы
и
называются перестановочными.
Свойства произведения матриц:
1)
,
где
-число;
2)
;
3)
;
4)
.
Единичной матрицей называется диагональная матрица, у которой все элементы равны 1.
.
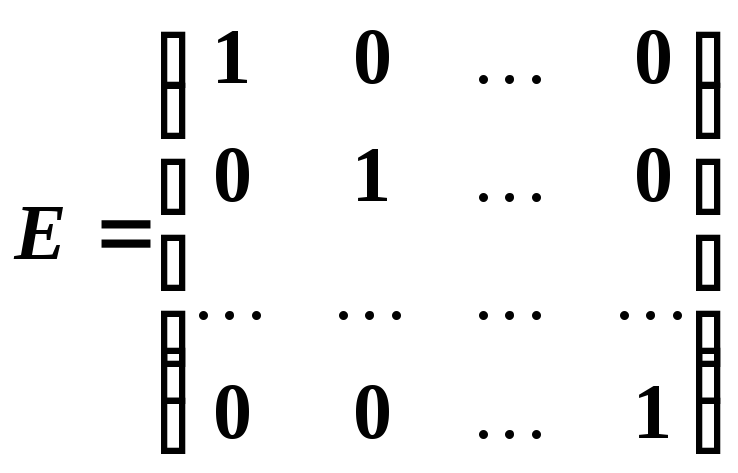Свойство
единичной матрицы:
для любой квадратной матрицы
.
Рассмотрим
произвольную квадратную матрицу
,
порядка
.
Если существует такая матрица
,
что
,
то говорят, что
обратима, а
называют обратной матрицей для матрицы
.