
- •1. Точные грани числовых множеств. Понятие точных граней ограниченного множества. Теорема существования точной верхней грани у множества, ограниченного сверху.
- •Определение сходящейся последовательности. Геометрический смысл определения.
- •Определение бесконечно малой последовательности. Геометрический смысл определения.
- •4. Определение бесконечно большой последовательности. Геометрический смысл определения.
- •5. Определение предела функции в точке по Коши. Геометрический смысл определения.
- •6. Определение предела функции в точке по Гейне.
- •7. Сравнение бесконечно малых величин. Порядок малости.
- •8. Определение функции, непрерывной в точке, по Коши.
- •9. Определение функции, непрерывной в точке, на языке приращений
- •10. Точки разрыва и их классификации.
- •11.Понятие дифференциала. Геометрический смысл дифференциала.
- •13Понятие предела фнп
- •14 Понятие частной производной фнп. Геометрический смысл
- •23 Понятие частной производной высшего порядка
- •24 Понятие дифференциала высшего порядка
- •25 Понятие частных производных высших порядков. Теорема
- •26 Точки локального экстремума фнп
- •Оглавление
8. Определение функции, непрерывной в точке, по Коши.
Функция f(x),
определённая в некоторой окрестности
точки х0
называется непрерывной в точке х0
если
 \
\

Функция f(x)
называется непрерывной в точке х0,
предельной
для области определения этой функции,
если для любого наперед заданного числа
 >0,существует
такое
>0,существует
такое
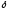 >0,что
для всех значений х из области определения
f(x),
для которых
>0,что
для всех значений х из области определения
f(x),
для которых
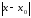 <
<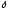 выполняется неравенство
выполняется неравенство
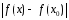 <
<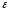 .
.
9. Определение функции, непрерывной в точке, на языке приращений
Пусть y=f(x)
непрерывна в точке
 и существует
и существует
 ,
,
 -
бесконечно малая, при
-
бесконечно малая, при
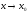 ,
то
,
то
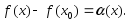
 -
это приращение функции.
-
это приращение функции.
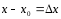 -
приращение аргумента.
-
приращение аргумента.
Функция y=f(x)
называется непрерывной в точке
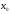 ,
если эта функция определена в какой-нибудь
окрестности точки
,
если эта функция определена в какой-нибудь
окрестности точки
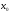 и если
и если
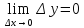 ,
т.е. если бесконечно малому
,
т.е. если бесконечно малому
приращению аргумента соответствует бесконечно малое приращение функции.
10. Точки разрыва и их классификации.
Если в какой-либо точке х0 функция не является непрерывной ,то точка х0 называется точкой разрыва функции, а сама функция разрывной в этой точке.
Различают 2 вида точек разрыва: точки разрыва первого рода и точки разрыва второго рода.
Если в точке разрыва х0 существуют конечные односторонние пределы функции, то разрыв функции называется разрывом первого рода.
Если при этом
f(x0-0)=f(x0+0) f(x0),
то х0
– точка устранимого разрыва, если
f(x0),
то х0
– точка устранимого разрыва, если
f(x0-0) f(x0+0),
то х0
– точка неустранимого разрыва первого
рода , а разность
f(x0+0),
то х0
– точка неустранимого разрыва первого
рода , а разность
f(x0 +0)-f(x0-0) называется скачком функции f(x) в точке х0.
11.Понятие дифференциала. Геометрический смысл дифференциала.
Дифференциал функции в некоторой точке – главная линейная часть приращения функции, равная произведению производной этой фунции в выбранной точке на приращение независимой переменной
Геометрически дифференциал равен приращению ординаты касательной, проведенной к графику функции в точке хо.
Производная же численно равна угловому коэффициенту касательной.
Рассмотрим ^М0КN:
tga=NK/M0N
=>f’(x0)=
NK/ x,
NK=
f’(x0)*
x,
NK=
f’(x0)*
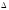 x
=> NK-это
диф-л ф-ции в тx0
x
=> NK-это
диф-л ф-ции в тx0
равен приращению, которое получает касательная, проведенная в точке М0, соответствующая приращению ^x

12Формула Тейлора (Маклорена) с остаточным членом в форме Пеано.
Если
y=f(x)
определена и n-раз
дифференцируема в
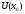 ,
то можно записать:
,
то можно записать:
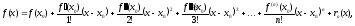 Остаточный член
в форме Пеано
Остаточный член
в форме Пеано
rn (x)=o((x-x0)n)
Теорема.
Если функция f(x)
определена и n
раз дифференцируема в окрестности точки
x0
, то при x
®
x0
имеет место формула 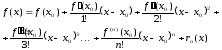
где rn (x)=o((x-x0)n) - остаточный член в форме Пеано.
Если взять в формуле Тейлора x0 = 0, то мы получим формулу Маклорена с остаточным членом в форме Пеано

13Понятие предела фнп
Пусть функция z = f(M) определена на множестве D, M(x1, x2,…,xn) Î Rn, M0(x10, x20,…,xn0).
Определение. (По Коши) Число А называют пределом функции z = f(M) в точке М0 (при M ®M0), если "e >0 $d>0 такое, что "MÎD, удовлетворяющей неравенству 0<r(M,M0)<d, выполняется неравенство |f(M) - A|<e.
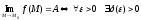
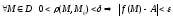
14 Понятие частной производной фнп. Геометрический смысл
Величина
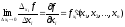 называется
частной производной от функции
u=f(x1,x2,…,xn)
по i-ой
переменной и обозначается символом
называется
частной производной от функции
u=f(x1,x2,…,xn)
по i-ой
переменной и обозначается символом
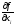 или символом
или символом
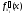 .
.
Геометрический смысл частных производных
Пусть
z = f(x, y),
(x, y)ÎD.
По
определению частной производной имеем:
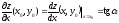 т.е.
т.е.
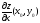 есть
тангенс угла наклона касательной к
графику
функции
есть
тангенс угла наклона касательной к
графику
функции
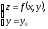 в
точке
(x0, y0,
z0),где
z0
= f(x0, y0).
Аналогично,
в
точке
(x0, y0,
z0),где
z0
= f(x0, y0).
Аналогично,
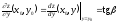 есть тангенс угла наклона касательной
к графику функции
есть тангенс угла наклона касательной
к графику функции
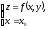 в
точке (x0, y0,
z0),
где
z0
= f(x0, y0),
в
точке (x0, y0,
z0),
где
z0
= f(x0, y0),
15 Определение ФНП, непрерывных в точке
Пусть множество D Ì Rn. Если каждой точке М(х1, х2, ..., хn) Î D поставлено в соответствие по некоторому правилу f число u Î R, то говорят, что на множестве D задана функция п переменных.
Обозначают: u = f(M), u = f(x1, x2, …, xn), f : Rn ®R.
16 Понятие дифференцируемой ФНП в точке.
Функция u=f( ,
,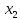 ,…
,…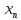 )
называется дифференцируемой в точке
M(
)
называется дифференцируемой в точке
M( ,
, ,…
,…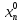 )
если её полное приращение в этой точке
имеет вид:
)
если её полное приращение в этой точке
имеет вид:
 или
или
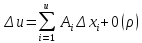
 где
где
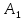 ,
i=1,2,…n – числа
,
i=1,2,…n – числа
 б.м.м. высшего порядка чем
б.м.м. высшего порядка чем
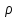
17 Понятие полного дифференциала
Главная, линейная
относительно приращений аргументов,
часть полного приращения функции z(x;y)
называется полным дифференциалом
функции и обозначается dz.
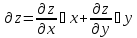
18 Теорема о достаточном условии дифференцируемости ФНП
Если функция u = f(x1, x2, …, xn) имеет частные производные по всем переменным в некоторой окрестности точки M0, причём эти производные непрерывны в точке M0, то функция u = f(x1, x2, …, xn) дифференцируема в точке M0.
19 Понятие касательной плоскости и нормали к поверхности в точке.
Касательной
плоскостью к поверхности в точке
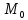 (
(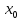 ;
;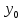 ;
;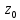 )
называется плоскость, в которой лежат
все касательные, проведенные к любой
кривой, принадлежащей поверхности и
проходящие через эту точку.
)
называется плоскость, в которой лежат
все касательные, проведенные к любой
кривой, принадлежащей поверхности и
проходящие через эту точку.

Нормалью
к поверхности в точке
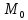 (
(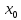 ;
;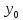 ;
; )
называется прямая, проходящая через
точку касания, перпендикулярно касательной
плоскости.
)
называется прямая, проходящая через
точку касания, перпендикулярно касательной
плоскости.
 =
= =
= или для неявно заданной
или для неявно заданной
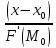 =
=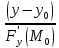 =
=
20 Понятие производной функции по направлению
Производной
скалярной функции U(x;y;z) по направлению
 в точке
в точке
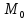 (
(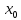 ;
; ;
; )
называется конечный предел отношения
приращения
)
называется конечный предел отношения
приращения
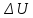 функции при перемещении из точки
функции при перемещении из точки
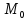 (
(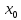 ;
;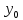 ;
; )
в направлении вектора
)
в направлении вектора
 к величине этого перемещения
к величине этого перемещения
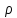 при
стремлении величины этого перемещения
к нулю.
при
стремлении величины этого перемещения
к нулю.
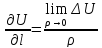
21 Теорема для вычисления производной по направлению
Если
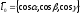 и u = u(M)
дифференцируема в точке
M0,
то
и u = u(M)
дифференцируема в точке
M0,
то

22 Понятие градиента. Свойства градиента
Градиентом
скалярного поля u
=
u(x,
y, z)
в точке M0
называется вектор
 .
.
Свойства:
1.
Градиент в данной точке M0
связан с производной по направлению
формулой
 .
.
2.
Градиент в данной точке M0
указывает направление наискорейшего
изменения поля в этой точке, а
 есть наибольшая скорость изменения
поля в точке M0
если направление
есть наибольшая скорость изменения
поля в точке M0
если направление
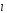 совпадает с
совпадает с
 (иначе наименьшее значение).
(иначе наименьшее значение).
3. Градиент в точке M0 направлен по нормали к поверхности уровня, проходящей через точку M0.
4. Производная по направлению вектора, касательного к поверхности уровня равна нулю.
