- •1. Точные грани числовых множеств. Понятие точных граней ограниченного множества. Теорема существования точной верхней грани у множества, ограниченного сверху.
- •Определение сходящейся последовательности. Геометрический смысл определения.
- •Определение бесконечно малой последовательности. Геометрический смысл определения.
- •4. Определение бесконечно большой последовательности. Геометрический смысл определения.
- •5. Определение предела функции в точке по Коши. Геометрический смысл определения.
- •6. Определение предела функции в точке по Гейне.
- •7. Сравнение бесконечно малых величин. Порядок малости.
- •8. Определение функции, непрерывной в точке, по Коши.
- •9. Определение функции, непрерывной в точке, на языке приращений
- •10. Точки разрыва и их классификации.
- •11.Понятие дифференциала. Геометрический смысл дифференциала.
- •13Понятие предела фнп
- •14 Понятие частной производной фнп. Геометрический смысл
- •23 Понятие частной производной высшего порядка
- •24 Понятие дифференциала высшего порядка
- •25 Понятие частных производных высших порядков. Теорема
- •26 Точки локального экстремума фнп
- •Оглавление
1. Точные грани числовых множеств. Понятие точных граней ограниченного множества. Теорема существования точной верхней грани у множества, ограниченного сверху.
Множество
действительных чисел А называется
ограниченным сверху (снизу), если
существует такое действительное число
М (число m),
что каждый элемент х А
удовлетворяет неравенству х
А
удовлетворяет неравенству х М(х
М(х m).
При этом число М (число m)
называется верхней гранью (нижней
гранью) множества А.
m).
При этом число М (число m)
называется верхней гранью (нижней
гранью) множества А.
Наименьшая из всех
верхних граней ограниченного сверху
множества А R
называется точной верхней гранью.
Другими словами, действительное число
М является точной верхней гранью
множества А
R
называется точной верхней гранью.
Другими словами, действительное число
М является точной верхней гранью
множества А R,
если
R,
если
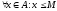 и
и
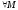 ’
< М
’
< М
 x0
>М’, x0
x0
>М’, x0 А.
А.
Наибольшая из всех
нижних граней ограниченного снизу
множества А R
называется точной нижней гранью. Другими
словами, действительное число m
является точной нижней гранью множества
А
R
называется точной нижней гранью. Другими
словами, действительное число m
является точной нижней гранью множества
А R,
если
R,
если
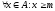 и
и
 ’
> m
’
> m
 x0
x0
 m’,
x0
m’,
x0 А.
А.
Множество, ограниченное сверху и снизу, называется ограниченным.
Определение сходящейся последовательности. Геометрический смысл определения.
Точка
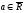 называется
пределом числовой последовательности
называется
пределом числовой последовательности
 при п
стремящемся
к бесконечности, если для любого ε>0
существует такой номер N,
что для всех номеров п>N
выполняется неравенство |xn-a|<ε
при п
стремящемся
к бесконечности, если для любого ε>0
существует такой номер N,
что для всех номеров п>N
выполняется неравенство |xn-a|<ε
Обозначение:
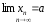

Кр.
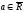 ,
,
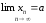
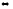
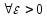

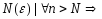 |xn-a|<ε
|xn-a|<ε
Если числовая последовательность имеет конечный предел, то она называется сходящейся.
N зависит от ε. Чем меньше ε, тем больше N. Исключение, когда последовательность состоит из одинаковых членов.



a- ε
a+ ε
a
Геометрически это означает, что, начиная с некоторого номера (п>N) все элементы последовательности находятся внутри ε-окр. точки а (U (a, ε))
Определение бесконечно малой последовательности. Геометрический смысл определения.
Последовательность
{xn}
называется
бесконечно-малой (б.м.п.), если
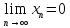 , то есть a=0
, то есть a=0
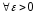

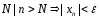



- ε
ε
0
Геометрически это означает, что, начиная с некоторого номера (п>N) все элементы последовательности находятся внутри ε-окр. точки 0 (U (0, ε))
4. Определение бесконечно большой последовательности. Геометрический смысл определения.
Говорят, что
последовательность имеет предел равный
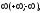 если для любого ε>0
существует такой номер N,
что для всех номеров п>N
выполняется неравенство
если для любого ε>0
существует такой номер N,
что для всех номеров п>N
выполняется неравенство
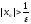
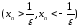
Обозначение.
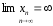 (
(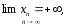
 )
)
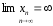
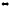
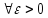

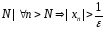
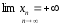
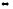
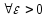


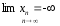
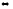
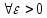


Если
предел числовой последовательности
равен
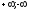 ,
то это бесконечно большая последовательность.
,
то это бесконечно большая последовательность.
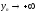 при
при
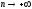

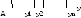
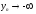 при
при
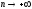

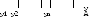
5. Определение предела функции в точке по Коши. Геометрический смысл определения.
Число A
называется пределом функции f(x)
в точке x=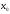 ,
если для любого
,
если для любого
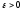

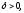 такое
что для всех
такое
что для всех

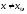 удовлетворяющих неравенству
удовлетворяющих неравенству
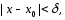 выполняется неравенство
выполняется неравенство
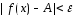
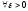

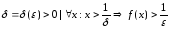
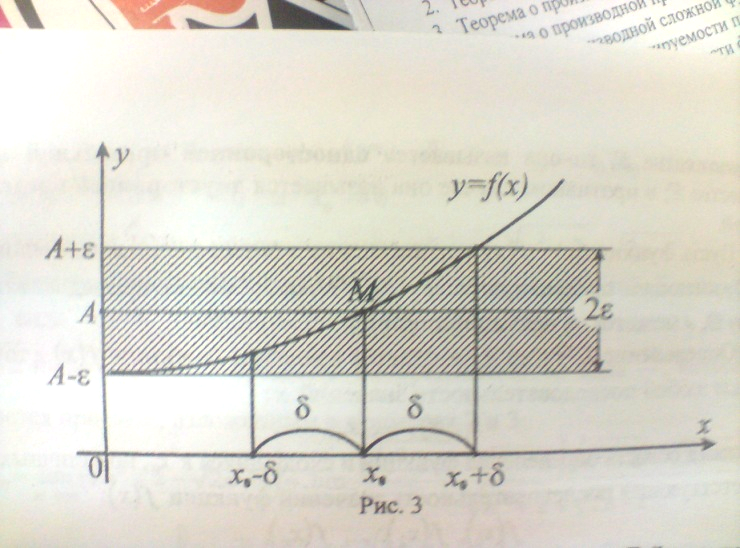
Если
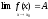 ,
то на графике функции y=f(x)
это иллюстрируется следующим образом:
,
то на графике функции y=f(x)
это иллюстрируется следующим образом:
Так
как из неравенства
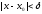 следует неравенство
следует неравенство
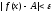 ,
то это значит, что для всех точек х,
отстоящих от точки
,
то это значит, что для всех точек х,
отстоящих от точки
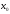 не далее, чем на
не далее, чем на
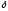 ,
точки М графика функции y=f(x)
лежат внутри полосы шириной
,
точки М графика функции y=f(x)
лежат внутри полосы шириной
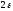 ,
ограниченной прямыми y=A-
,
ограниченной прямыми y=A- и y=A+
и y=A+ .
.
6. Определение предела функции в точке по Гейне.
Число A
называется пределом функции f(x)
в точке x=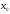 ,
если для любой сходящейся к
,
если для любой сходящейся к
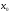 последовательности
последовательности
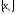 значений аргумента х,
отличных от
значений аргумента х,
отличных от
 соответствующая последовательность
значений функции f(
соответствующая последовательность
значений функции f(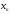 )
сходится к числу А.
)
сходится к числу А.
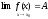
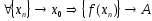
7. Сравнение бесконечно малых величин. Порядок малости.
Функция α(х) называется б.м. функцией при х -> a (или в окрестности точки а),если limα(x)=0.
x->a
Две б.м. α и β называются бесконечно малыми одного порядка, если предел их отношения равен некоторому числу, отличному от нуля, т.е. если lim(α/β)=A ≠ 0.
x->a
Две б.м. α и β называются эквивалентными если предел их отношения равен 1, т.е. :
lim(α/β)=1 α~β
x->a
Если lim(α/β)=0 (a lim(β/α)=∞), то α называется б.м. высшего порядка малости по
x->a x->a
сравнению с бесконечно малой β, напротив,β называется при этой бесконечно малой низшего порядка малости по сравнению с α .
Бесконечно малая α называется б.м. к-го порядка по отношению к б.м. β, если α и βк будут бесконечно малыми одного порядка, т.е. lim (α/βk)=A ≠ 0.
x->a
Если отношение α/β при x->a не стремится ни к какому пределу; ни к конечному, ни к бесконечному, то говорят, что б.м. α и β несравнимы между собой.
Таблица э.м.ф.
-
sinα(x)~α(x)
-
tgα(x)~α(x)
-
1 – cosα(x)~
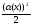
-
arcsinα(x)~α(x)
-
arctgα(x)~α(x)
-
ln(1+α(x))~α(x)
-
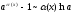 (a>0)
(a>0)
eα(x)-1~α(x)
-
(1+
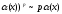 )
)
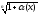 -1~
-1~