35. Уравнение теплопроводности в объемной области. Случай прямоугольных координат.
Вывод дифференциального уравнения сделаем упрощенным методом [4]. Предположим, что имеется одномерное температурное поле (тепло распространяется в одном направлении, например в направлении оси x). Термические коэффициенты считаем независимыми от координат и времени.
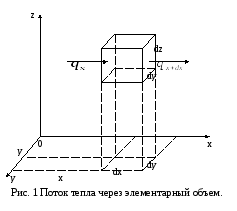
Выделим в однородной и изотропной
неограниченной пластине элементарный
параллелепипед, объем которого равен
dxdydz (Рис. 1).
Количества тепла, втекающего через
левую грань dydz в
параллелепипед в единицу времени, равно
,
а количества тепла, вытекающее через
противоположную грань в единицу времени,
равно
.
Если
,
то элементарный параллелепипед будет
нагреваться, тогда разница между этими
потоками тепла по закону сохранения
энергии равна теплу, аккумулированному
данным элементарным параллелепипедом,
т. е.
(1.1)
Величина
есть неизвестная функция x.
Если ее разложить в ряд Тейлора и
ограничиться двумя первыми членами
ряда, то можно написать:
.
Тогда из равенства (1.1) будем иметь:
.
Применяя уравнение теплопроводности
, получим
или
.
(1.2)
Уравнение (1.2) есть дифференциальное уравнение теплопроводности для одномерного потока тепла. Если тепло распространяется по нормали к изометрическим поверхностям, то вектор q можно разложить на три составляющие по координатным осям. Количество аккумулированного элементарным объемом тепла будет равно сумме
.
Тогда дифференциальное уравнение примет вид
.
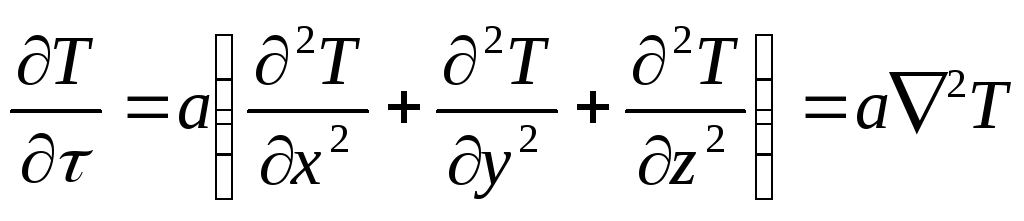(1.3)
где
- оператор Лапласа.
36. Изобарный процесс водяного пара
Изобарный процесс (p =const).
