
- •3. Основные свойства неопределённого интеграла
- •4. Интегрирование методом замены переменного
- •5. Интегрирование по частям
- •6. Интегрирование рациональных функций Интегрирование рациональной функции
- •7. Интегрирование тригонометрических функций
- •8. Интегрирование некоторых иррациональных функций
- •9. Определённый интеграл
- •10. Несобственные интегралы
- •11. Вычисление площадей плоских фигур
11. Вычисление площадей плоских фигур
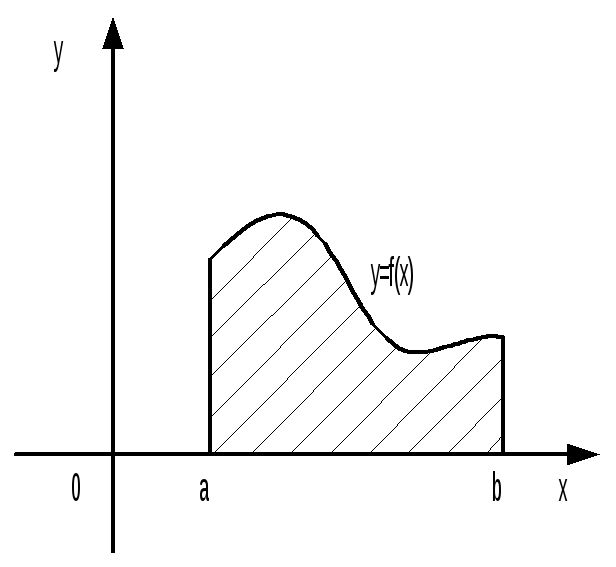
Площадь криволинейной
трапеции, ограниченной графиками функций
x
= a,
x
= b,
y
= 0, y
= f(x)
(f(x)
0 при x
[a;
b]),
находится по формуле
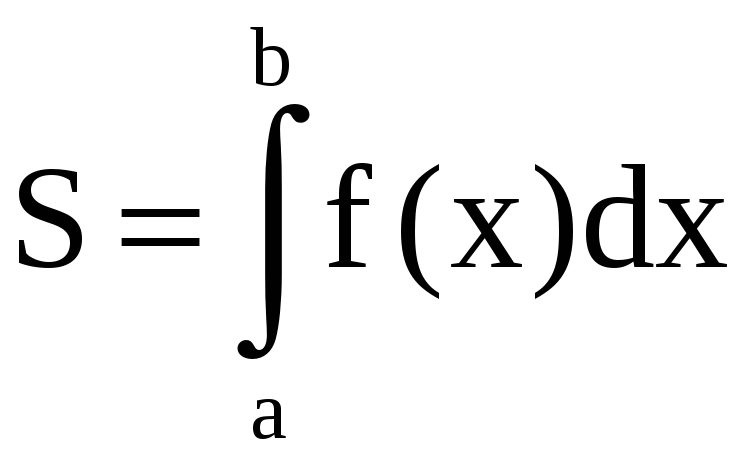 .
.
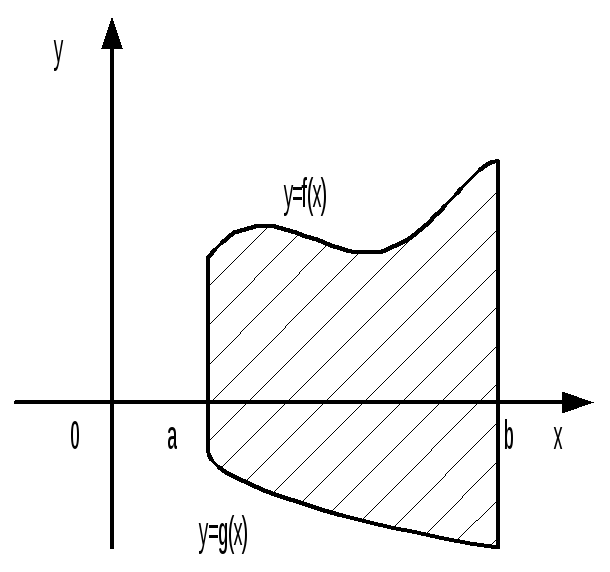
Если фигура (D) ограничена графиками функций x = a, x = b, y = f(x),
y = g(x), f(x)
g(x), при x
[a; b], то площадь S фигуры (D) находится по
формуле
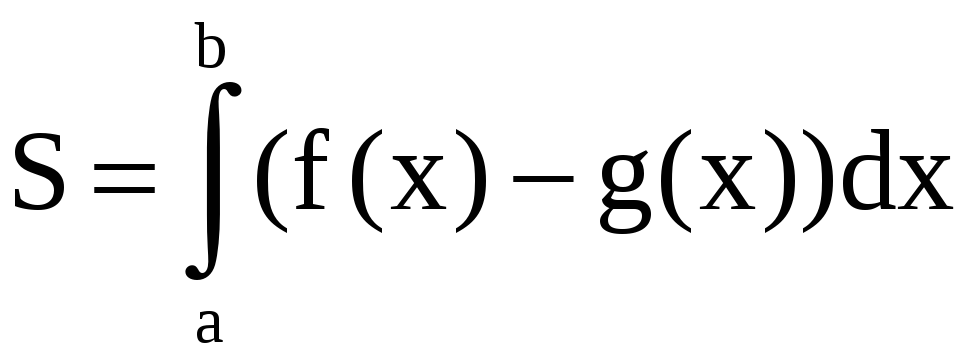 .
.
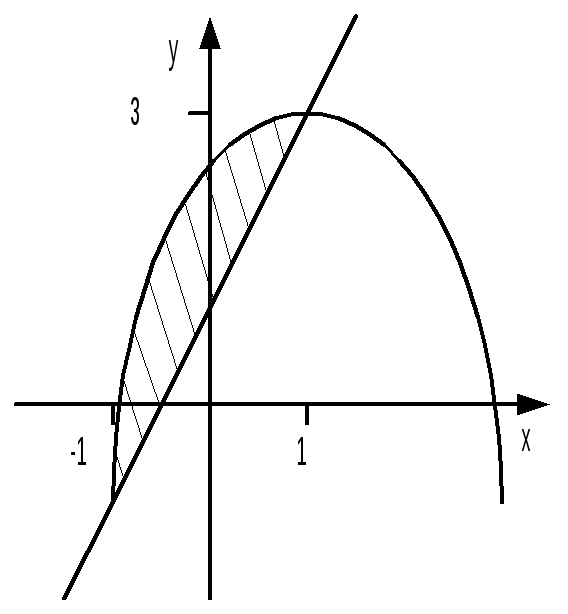
Пример 23. Найти площадь S фигуры (D), ограниченной линиями y = –x2 + 2x + 2 и y = 2x + 1.
Решение. Найдём абсциссы точек пересечения графиков функций, для чего решим уравнение: –x2 + 2x + 2 = 2x + 1; x2 – 1 = 0; x1 = –1,
x2 = 1. Для всех точек x из отрезка [–1; 1] –x2 + 2x + 2 2x + 1. Поэтому
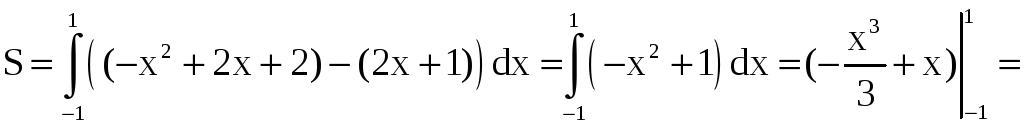
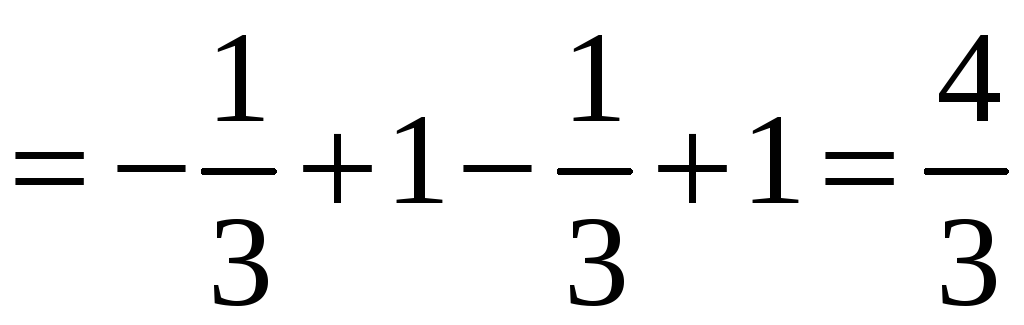 .
.
П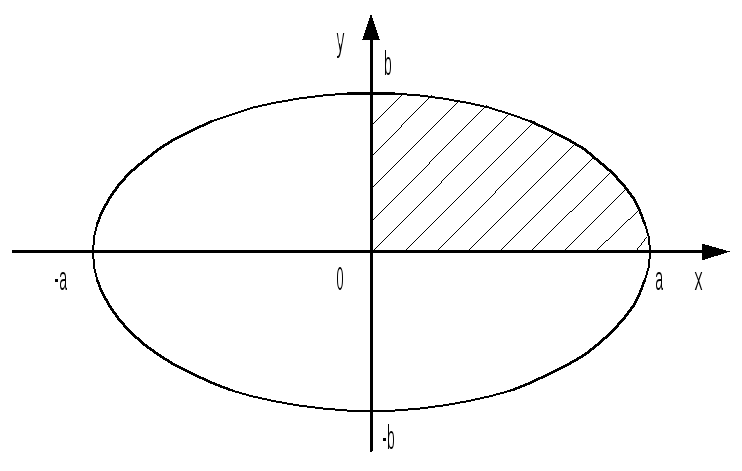 ример 24.
Найти площадь фигуры, ограниченной
эллипсом
ример 24.
Найти площадь фигуры, ограниченной
эллипсом
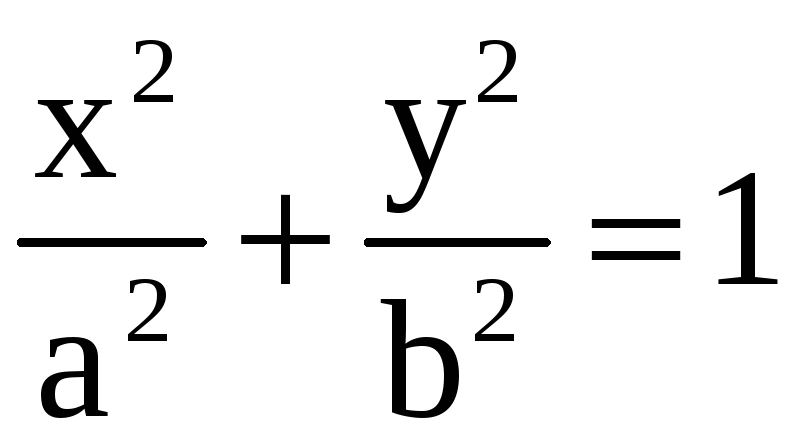 .
.
Решение.
Эллипс имеет две оси симметрии:
координатные оси 0х и 0у. Поэтому площадь
S фигуры равна учетверённой площади S1
части (D1)
фигуры, расположенной в первой четверти
(заштриховано). Фигура (D1)
ограничена сверху линией
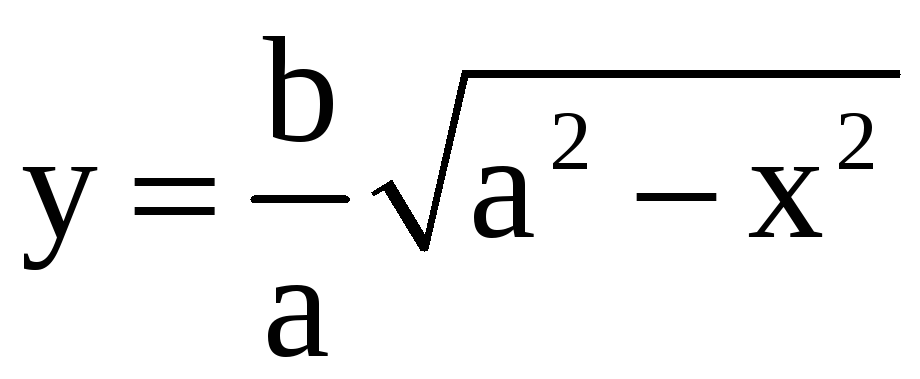 ,
снизу – осью 0х, слева – осью 0у. Поэтому
,
снизу – осью 0х, слева – осью 0у. Поэтому
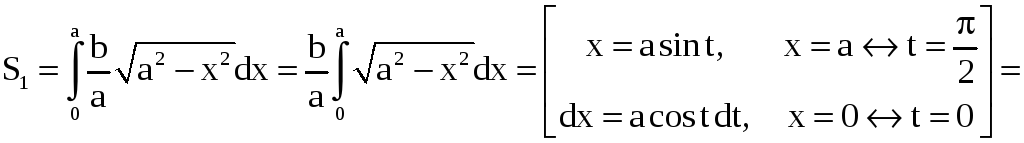
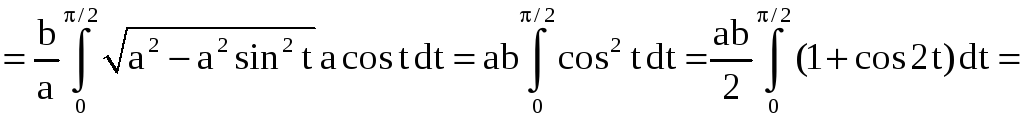
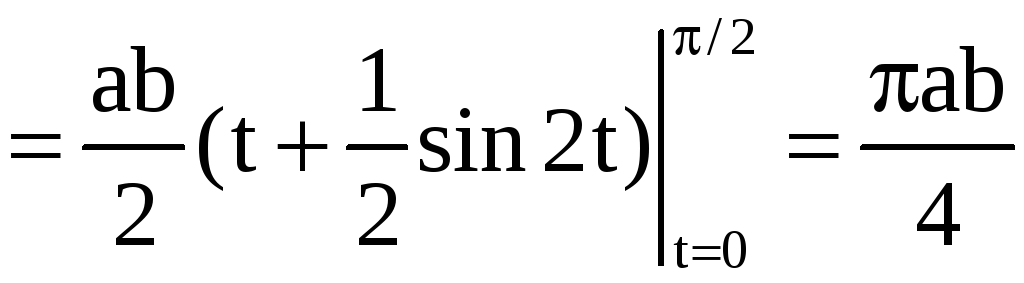
 .
.
Отсюда находим S = 4S1 = ab.
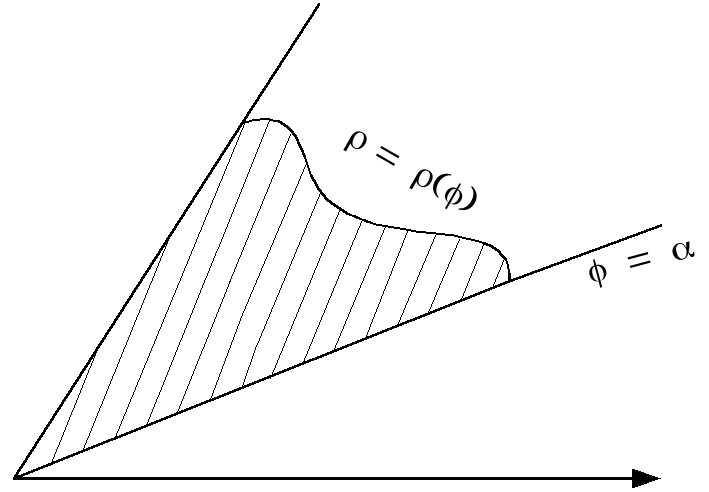
Площадь S
криволинейного сектора, ограниченного
графиком функции
![]() и лучами
и лучами
![]() и
и
![]() в полярной системе координат, находится
по формуле
в полярной системе координат, находится
по формуле
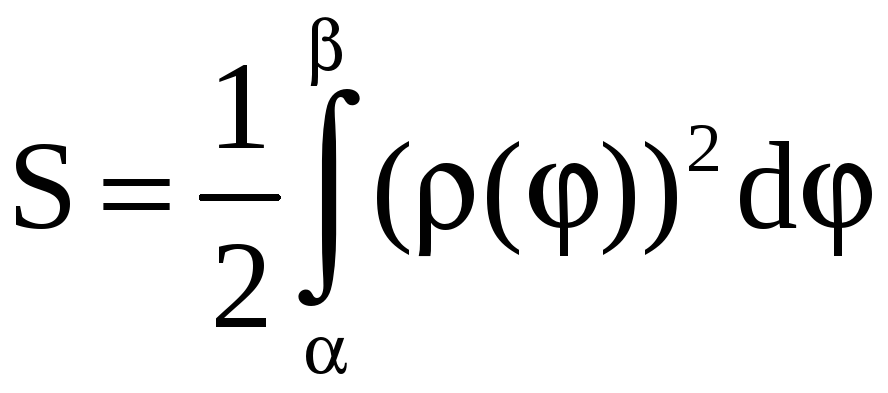 .
.
Пример 25.
Найти площадь S фигуры, ограниченной
линией, заданной в полярной системе
координат уравнением
![]() .
.
Решение.
Начнём с изображения линии. Так как
![]() ,
то нам нужно сначала решить неравенство
,
то нам нужно сначала решить неравенство
![]() .
Имеем
.
Имеем
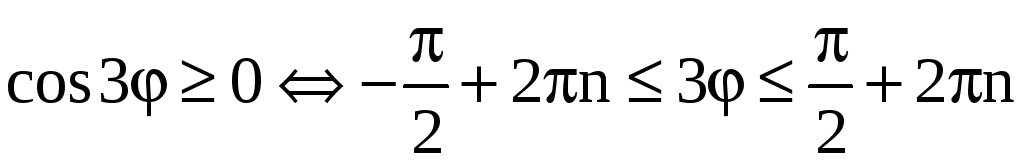
 ,
,
![]()
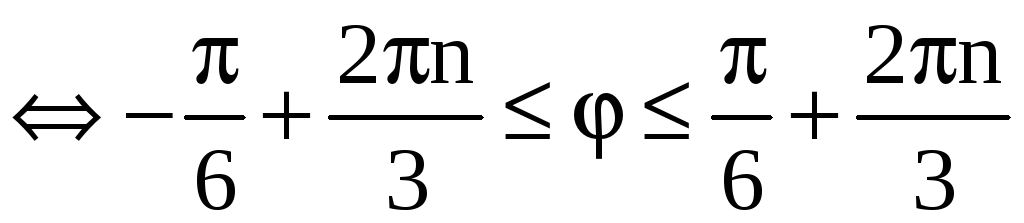 ,
,
![]() .
.
При n = 0:
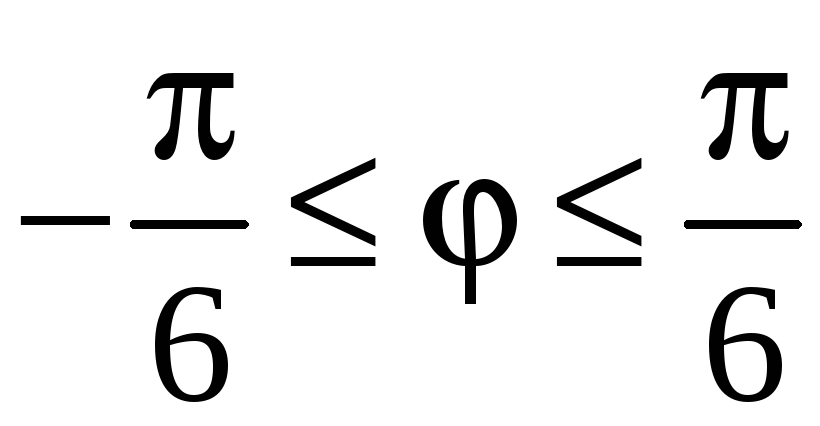 ;
;
при n = 1:
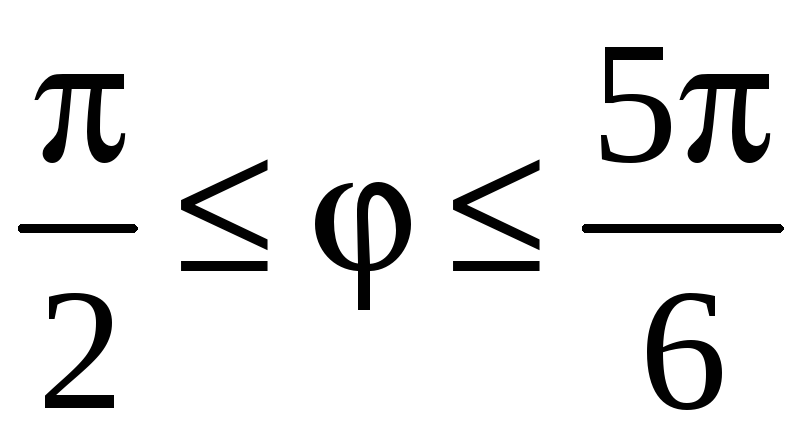 ;
;
при n = 2:
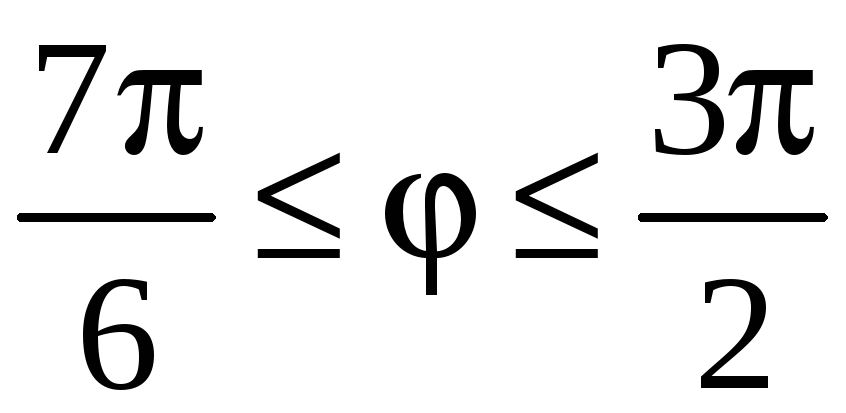 ;
;
при n = 3:
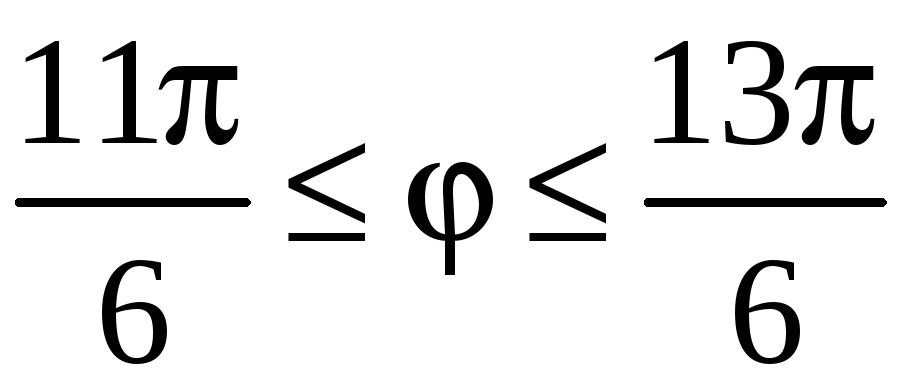 – этот угол является повторением угла,
соответствующего значению n = 0. Рассмотрение
других значений приводит к уже полученным
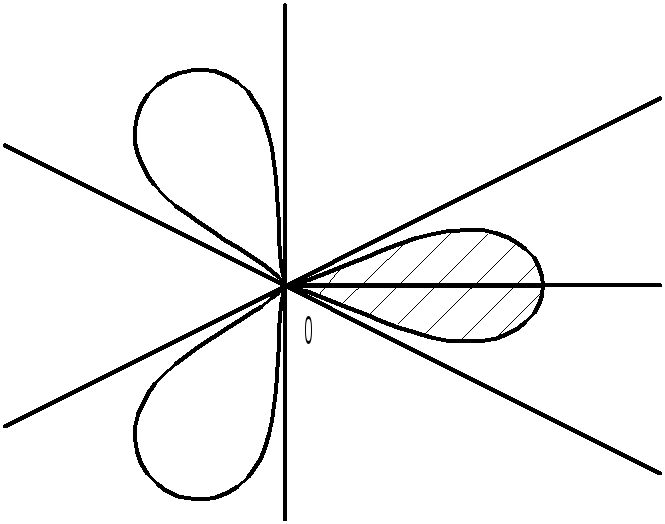
углам на плоскости. Рассмотрим рисунок.
Наша фигура ограничена тремя лепестками.
Её площадь S равна 3S1,
где S1
– площадь одного лепестка (заштриховано).
– этот угол является повторением угла,
соответствующего значению n = 0. Рассмотрение
других значений приводит к уже полученным
углам на плоскости. Рассмотрим рисунок.
Наша фигура ограничена тремя лепестками.
Её площадь S равна 3S1,
где S1
– площадь одного лепестка (заштриховано).
Имеем
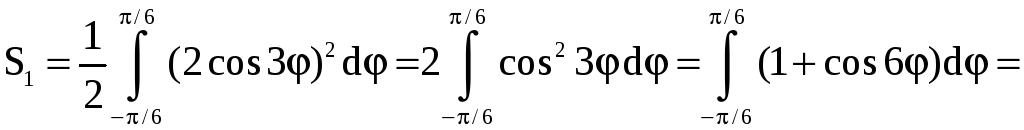
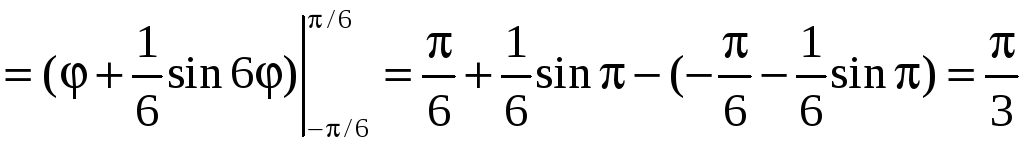 .
.
