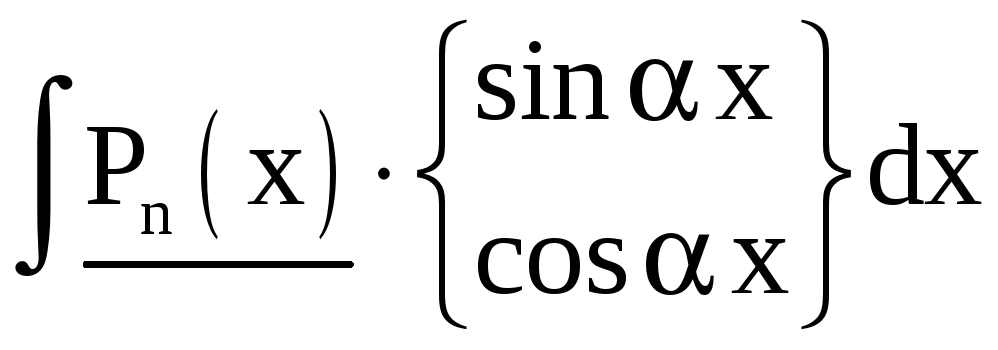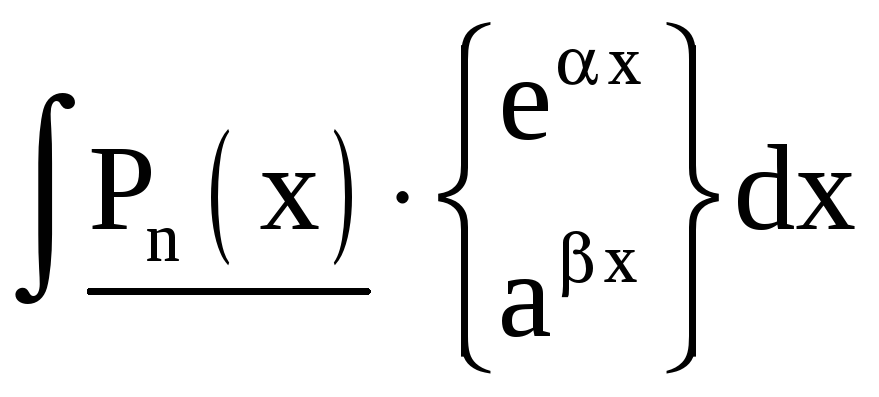- •3. Основные свойства неопределённого интеграла
- •4. Интегрирование методом замены переменного
- •5. Интегрирование по частям
- •6. Интегрирование рациональных функций Интегрирование рациональной функции
- •7. Интегрирование тригонометрических функций
- •8. Интегрирование некоторых иррациональных функций
- •9. Определённый интеграл
- •10. Несобственные интегралы
- •11. Вычисление площадей плоских фигур
 ,
, 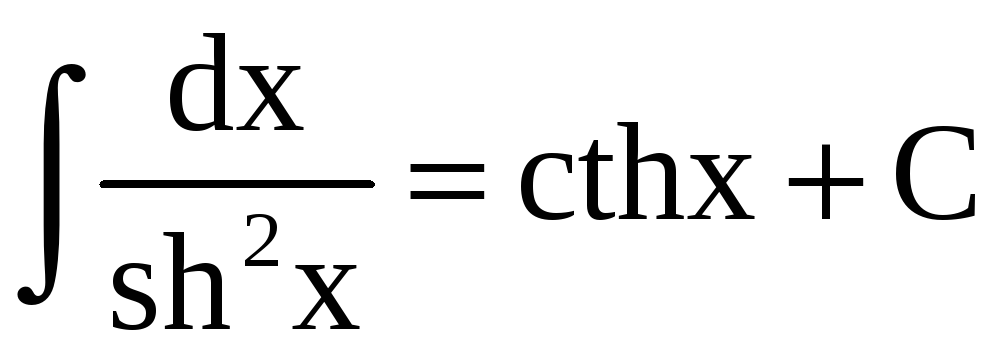 .
.
3. Основные свойства неопределённого интеграла
-
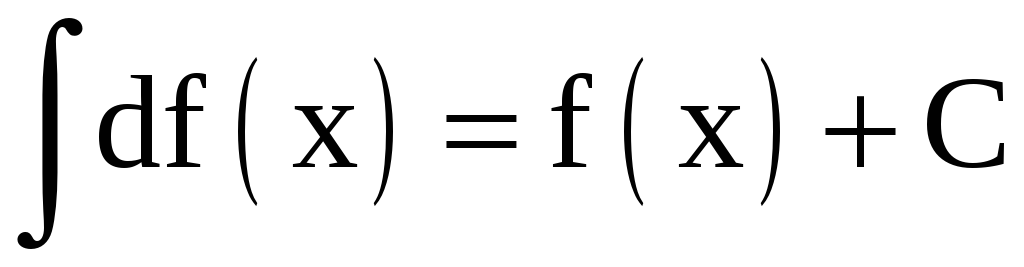 ;
; -
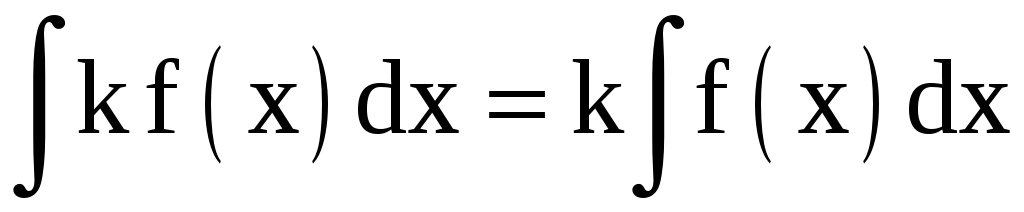 ,
где k – постоянная величина;
,
где k – постоянная величина; -
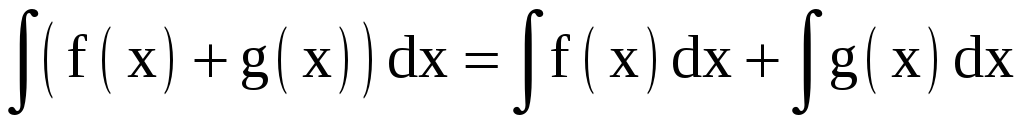 .
.
(свойства 2 и 3 составляют так называемое свойство линейности).
Пример 1.
Найти
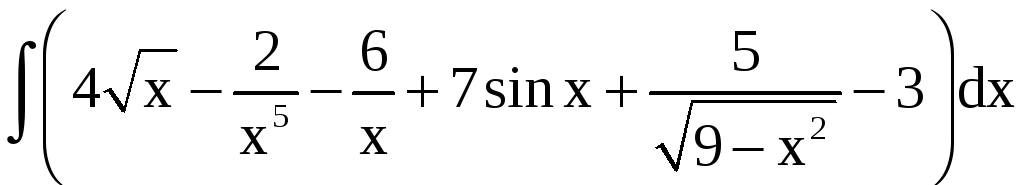 .
.
Решение.
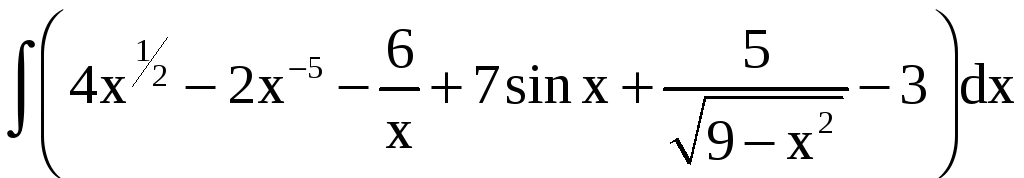 =
=
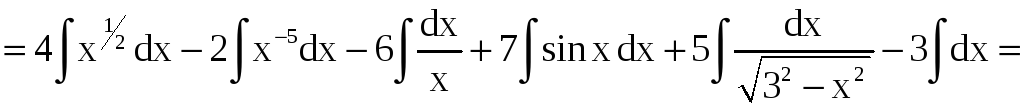
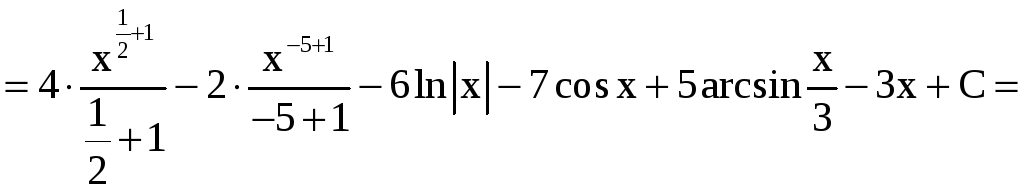
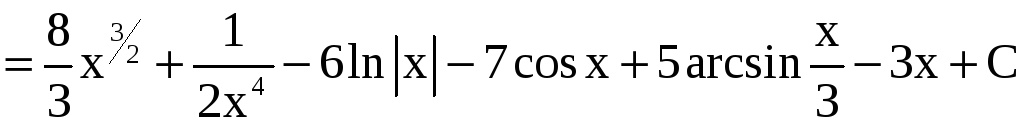 .
.
4. Интегрирование методом замены переменного
Теорема 1. Если F(x) – первообразная функции f(x), то при условии и дифференцируемости функции (x) справедлива формула
![]()
или
![]() .
.
Пример 2.
Найти интегралы: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)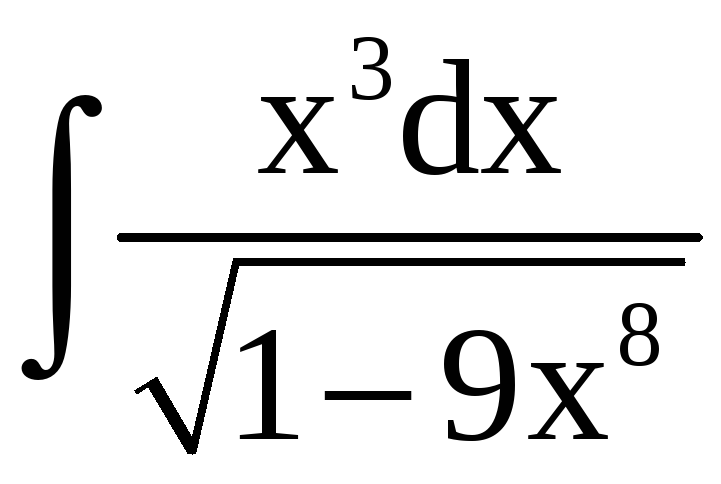 .
.
Решение.
а)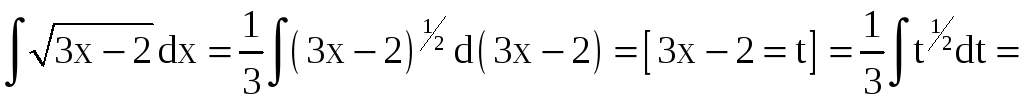
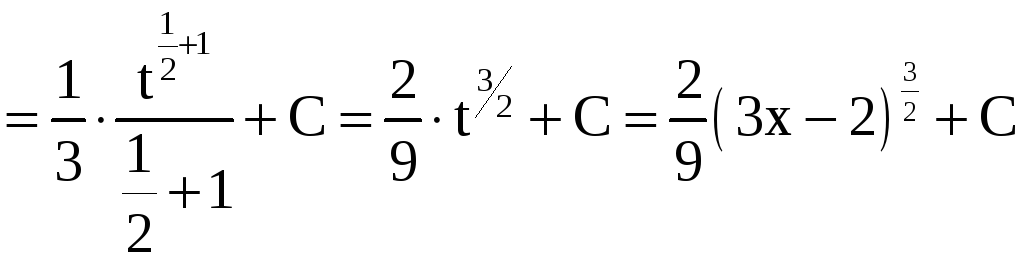 ;
;
б)

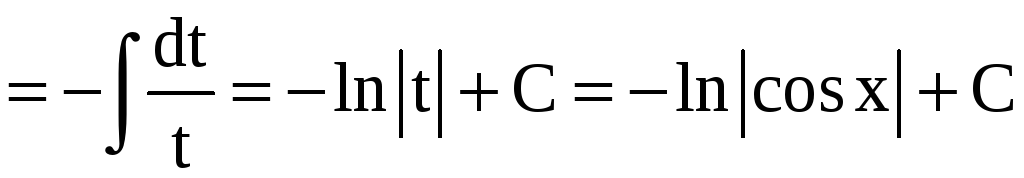 ;
;
в)

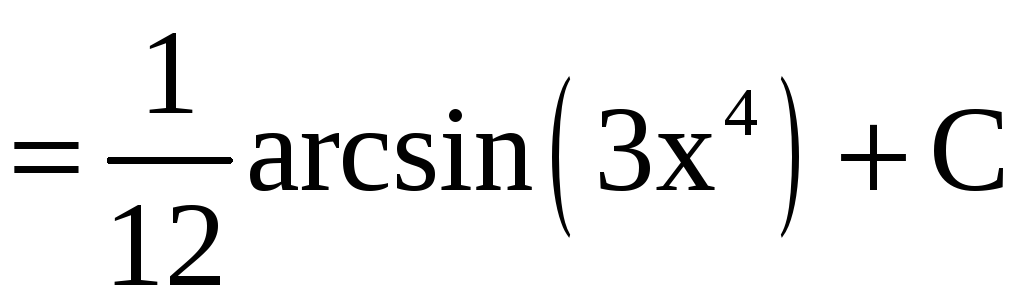 .
.
Пример 3.
Найти
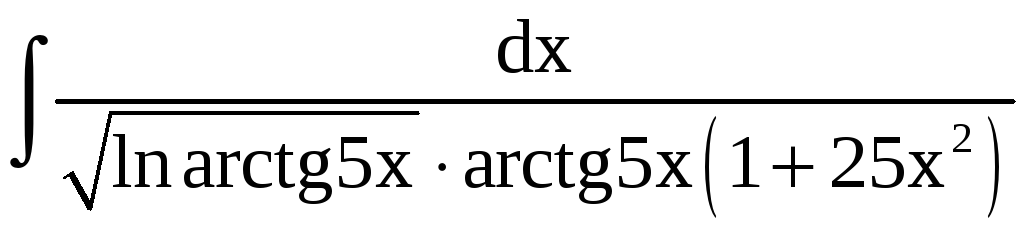 .
.
Решение.
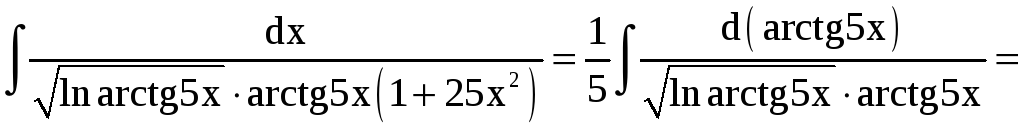
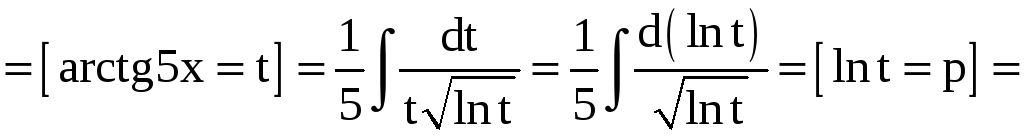
![]()
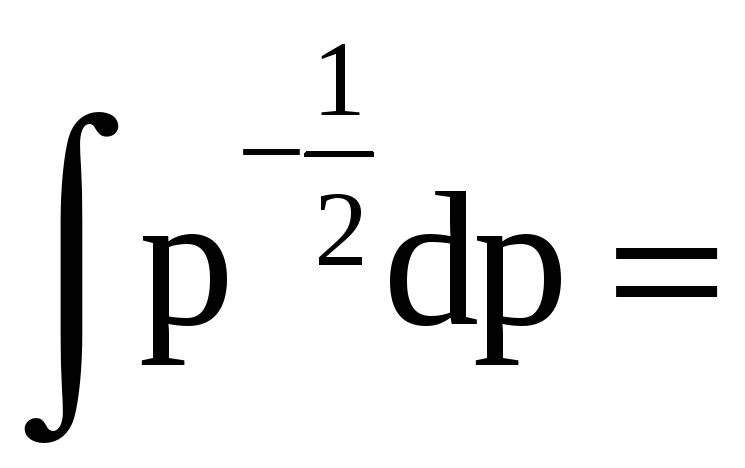
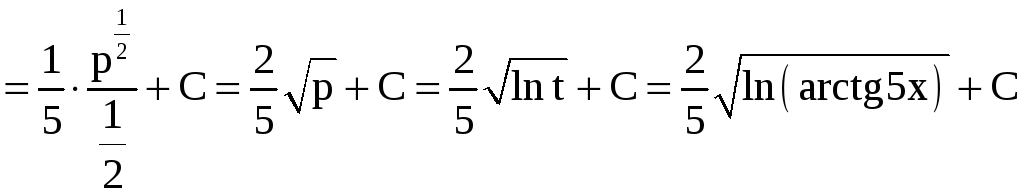 .
.
Пример 4.
Найти
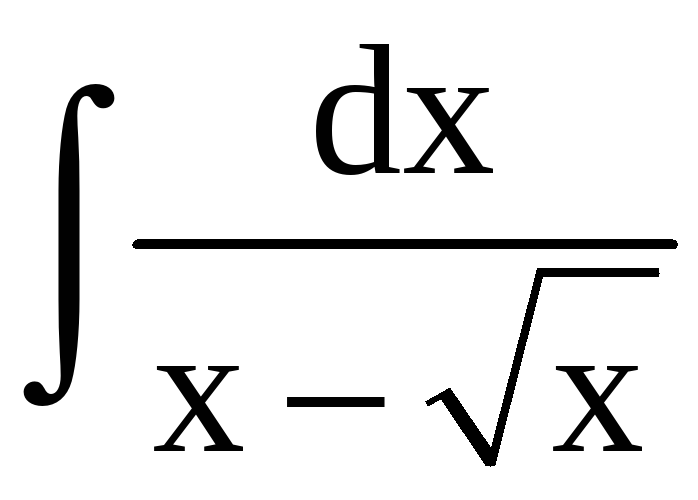 .
.
Решение.
Положим
![]() .
.
Тогда
![]() и
и
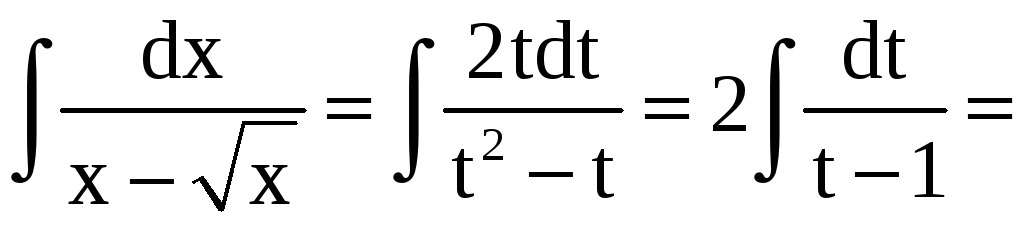
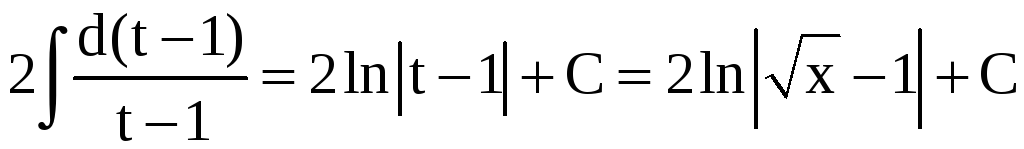
Пример 5.
Найти
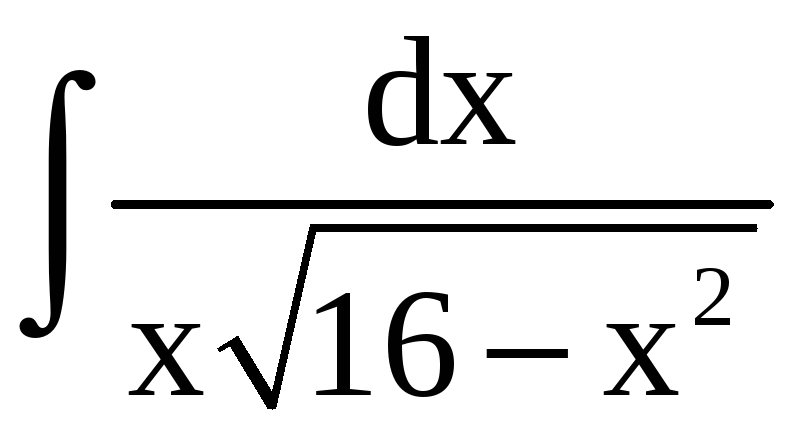 .
.
Решение.
Применим подстановку
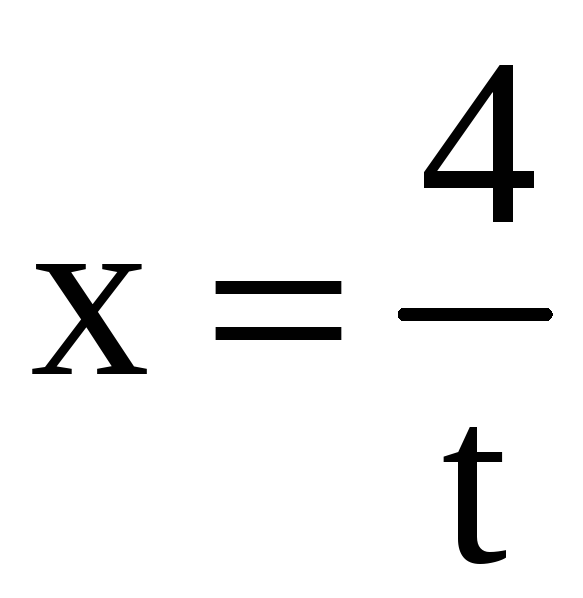 .
.
Тогда
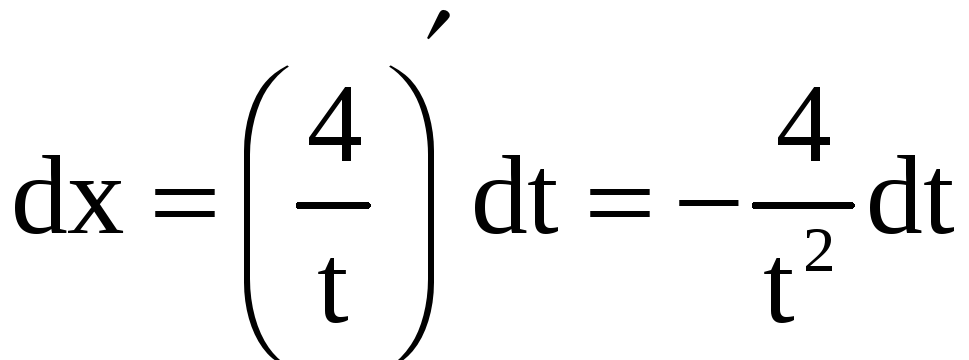 .
.
Имеем
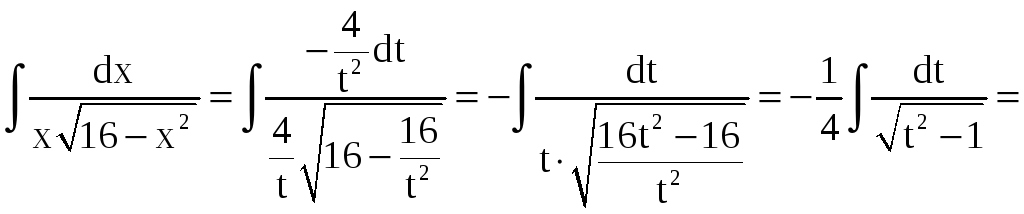
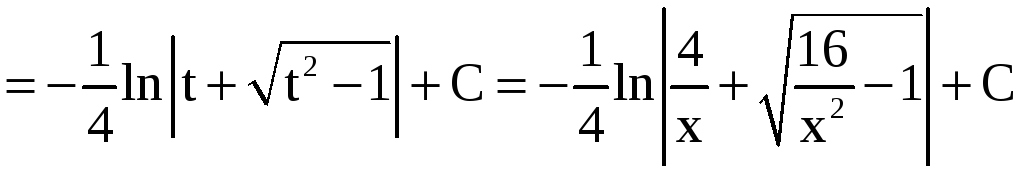 .
.
5. Интегрирование по частям
Если u(x), v(x) дифференцируемы, то справедлива формула интегрирования по частям
![]() .
.
Эту формулу следует применять в тех случаях, когда подынтегральное выражение vdu проще исходного выражения udv.
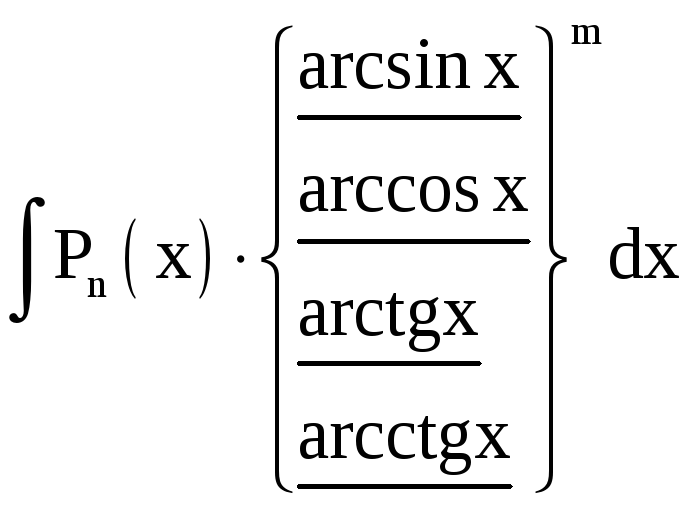
Ниже приведены основные типы интегралов, берущихся по частям.
|
I тип |
II тип |
III тип (интегралы, приводящиеся к себе) |
|
|
|
|
За u принимаются
подчёркнутые функции, за dv – остальная
часть подынтегрального выражения. Pn
(x) – многочлен степени n. Интегралы I
типа берутся путём интегрирования по
частям n раз, II типа – m раз, III типа (за
исключением двух последних) – 2 раза
(причём, в первом интеграле III типа оба
раза за u можно принять как
![]() ,
так и тригонометрические функции
,
так и тригонометрические функции
![]() ,
,
![]() ).
).
По частям могут быть взяты и интегралы, не вошедшие в эту таблицу.
Пример 6. Найти интегралы:
а)![]() ; б)
; б)![]() ; в)
; в)
![]() .
.
Решение. а)
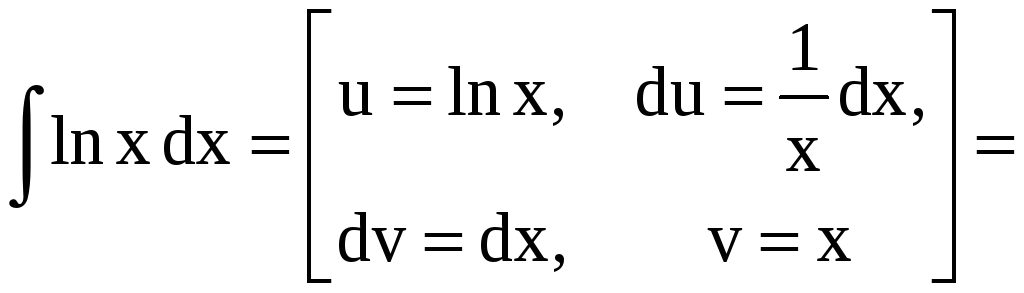
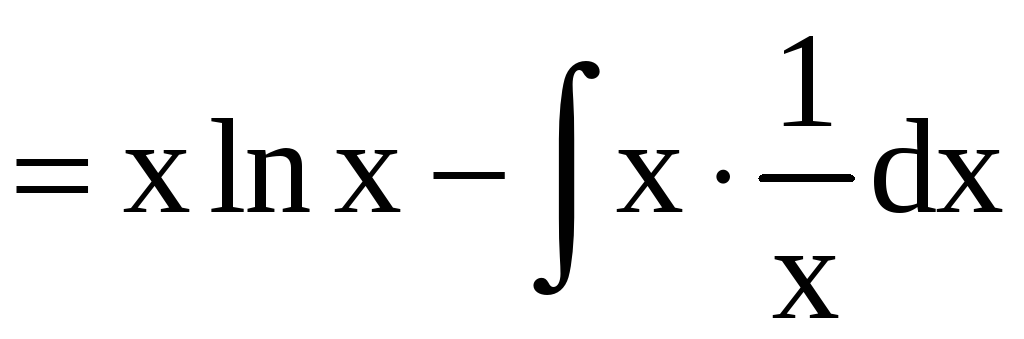
![]() .
.
Здесь и ниже при нахождении v при известном dv мы полагаем С = 0 (как в этом случае: dv = dx, отсюда следует v = x + C, но мы берём одну из первообразных v = x).
б)
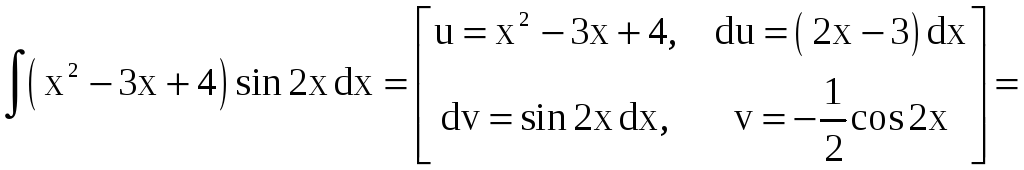
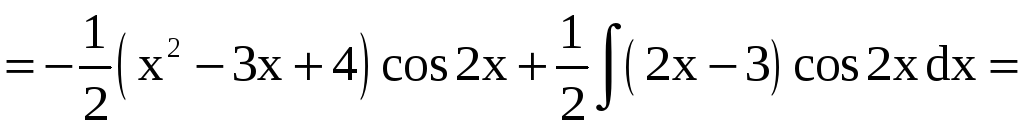
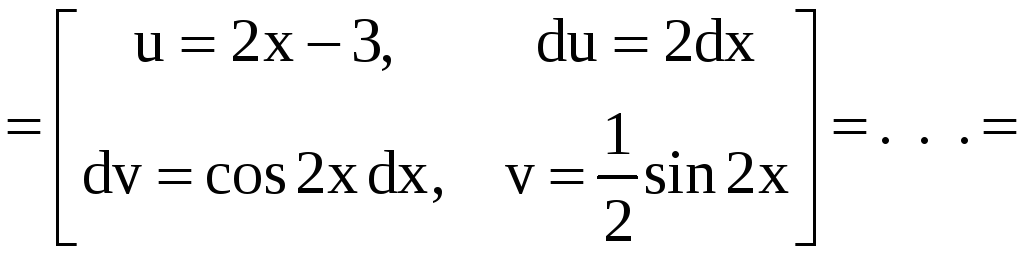
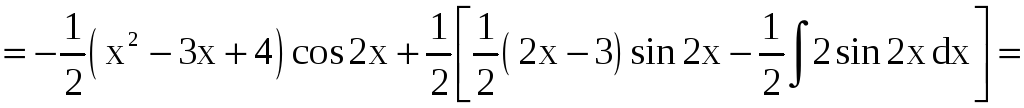
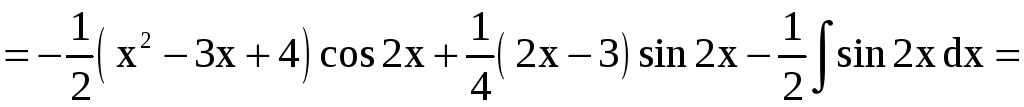
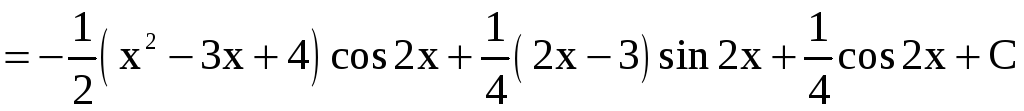 .
.
в) Обозначим
![]() .
Имеем
.
Имеем
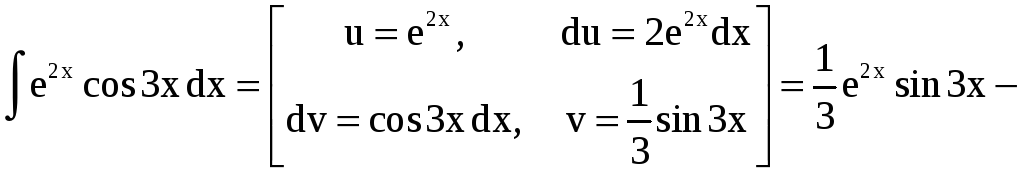
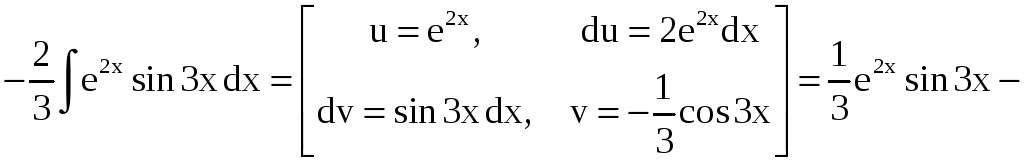
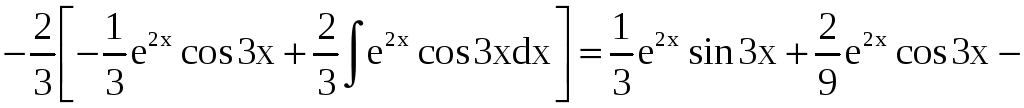
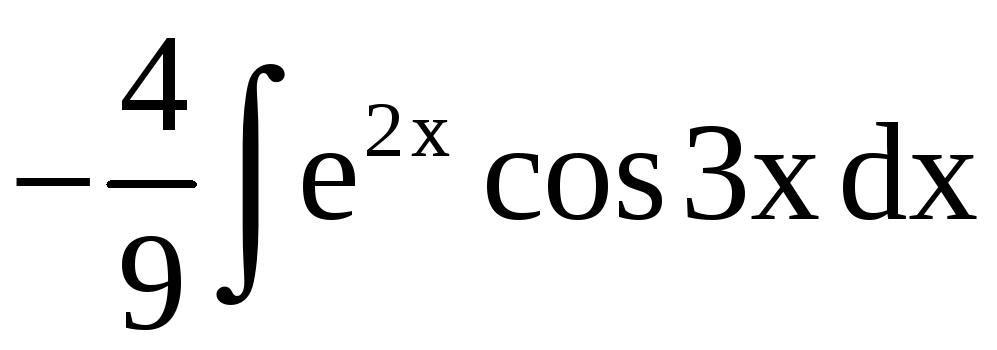 .
.
Получается, что
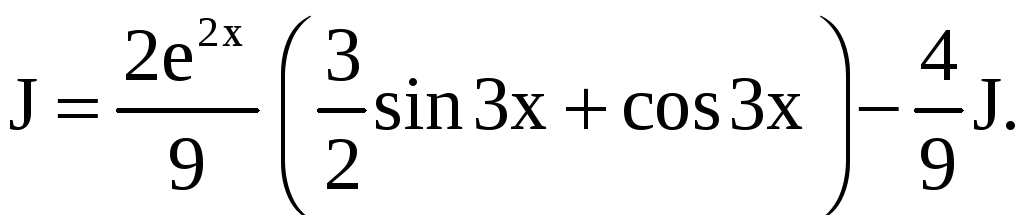
Отсюда находим (учитывая, что J является семейством функций, отличающихся друг от друга на постоянную величину)
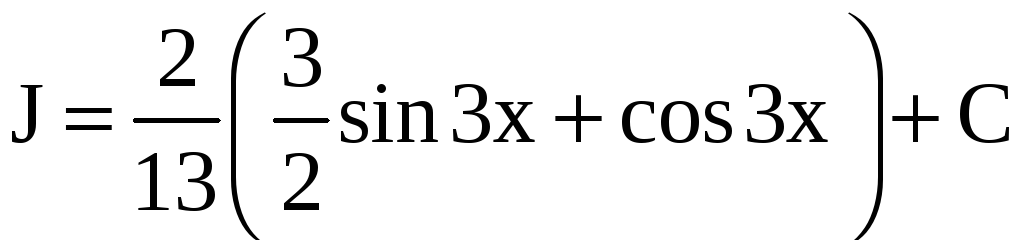 .
.
6. Интегрирование рациональных функций Интегрирование рациональной функции
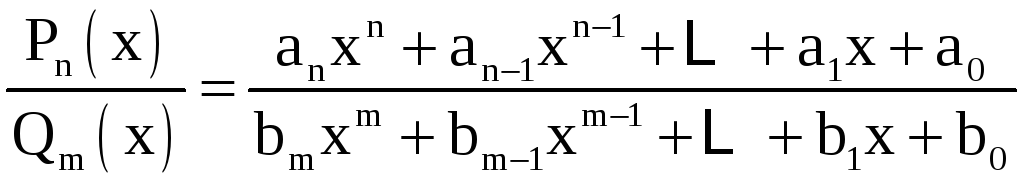 ,
, ![]() , являющейся
правильной дробью (т.е. при
, являющейся
правильной дробью (т.е. при
![]() ),
производится путём представления этой
функции в виде суммы простых дробей.
Если же дробь является неправильной
(
),
производится путём представления этой
функции в виде суммы простых дробей.
Если же дробь является неправильной
(![]() ),
то её представляют в виде суммы многочлена
и правильной дроби, затем интегрируют
эти слагаемые.
),
то её представляют в виде суммы многочлена
и правильной дроби, затем интегрируют
эти слагаемые.
Пример 7.
Найти интегралы: а)
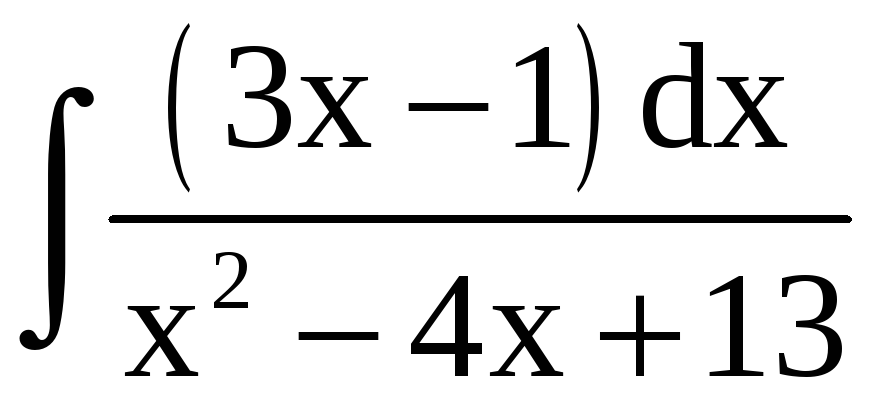 ; б)
; б)
 .
.
Решение.
а)
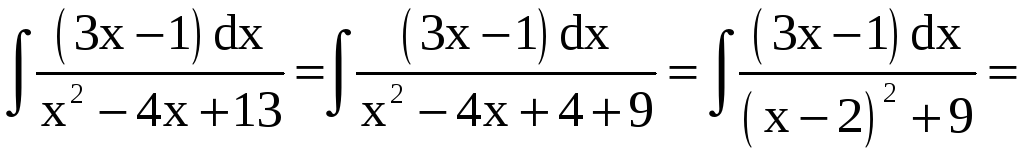
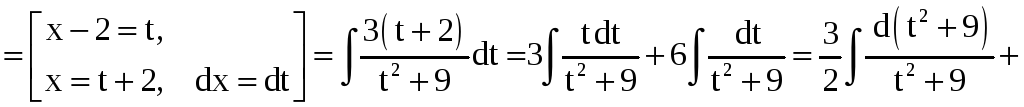
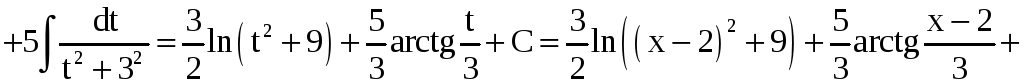
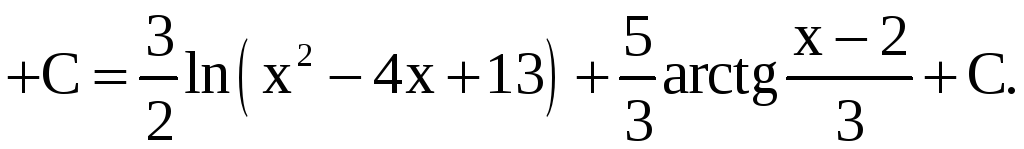
б)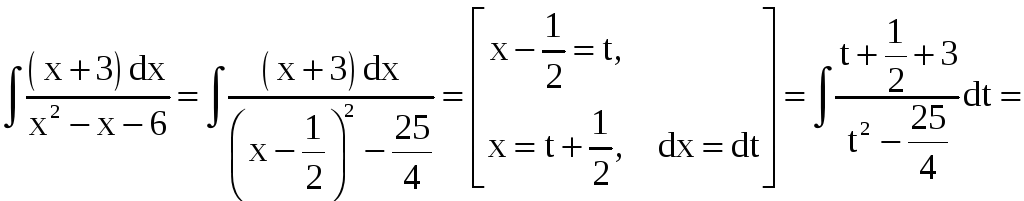

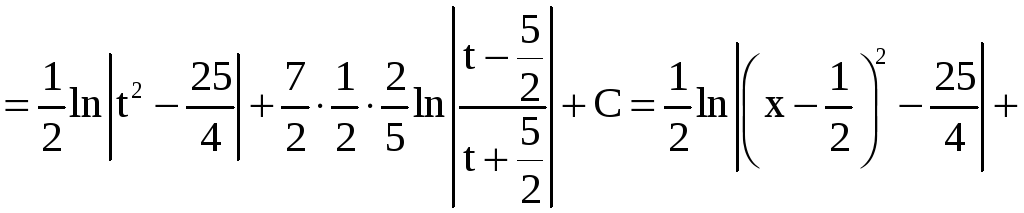
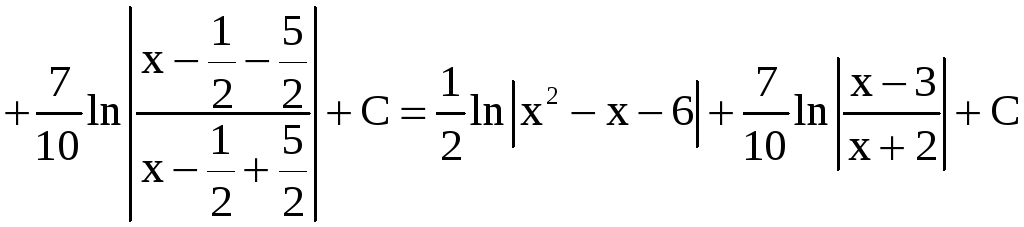 .
.
Пример 8. Найти
интегралы: а)
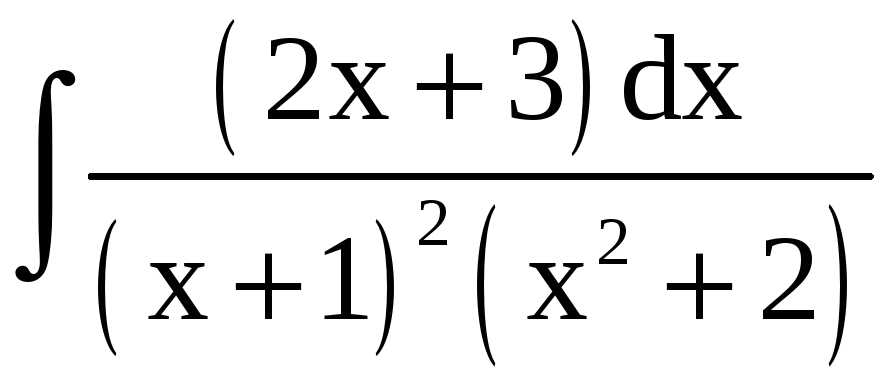 ;
;
б)
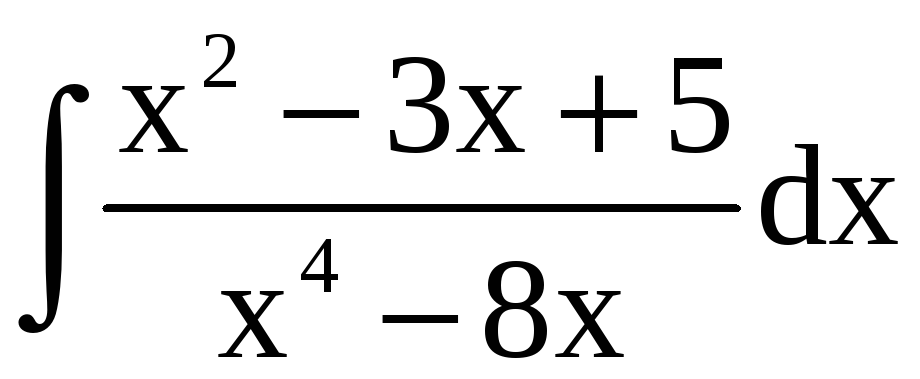 ; в)
; в)
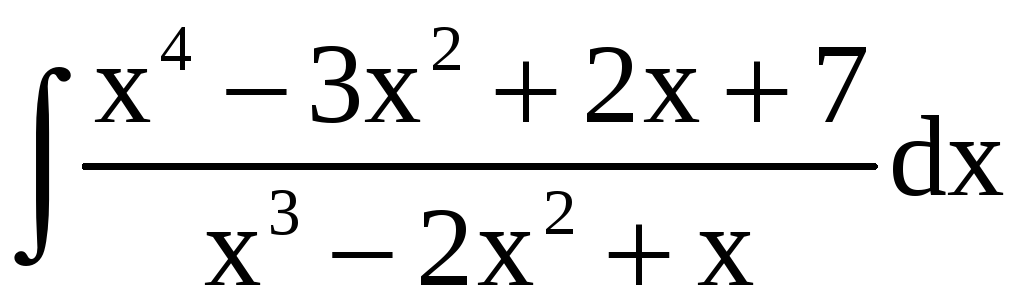 .
.
Решение. а) Найдём
разложение подынтегральной функции
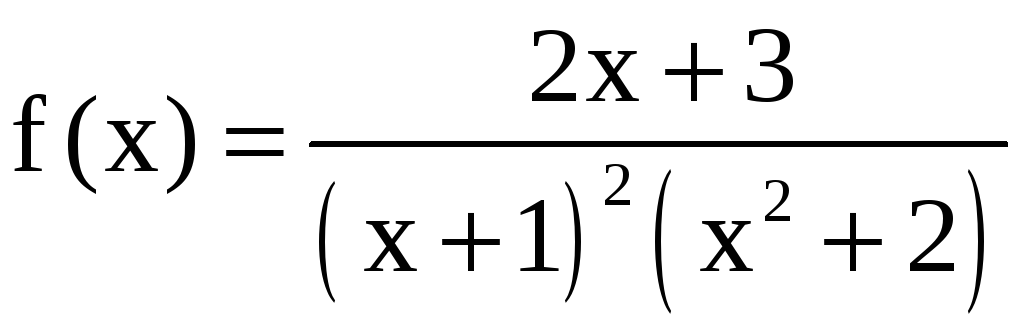 на сумму простых дробей:
на сумму простых дробей:
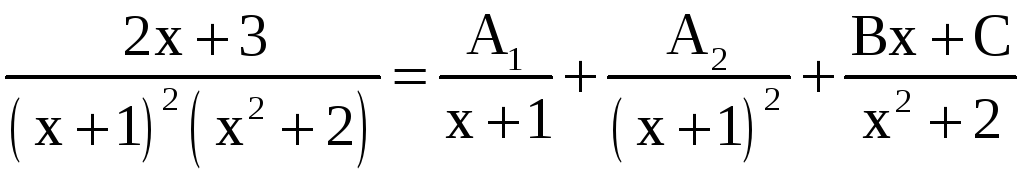 ;
;
![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]()
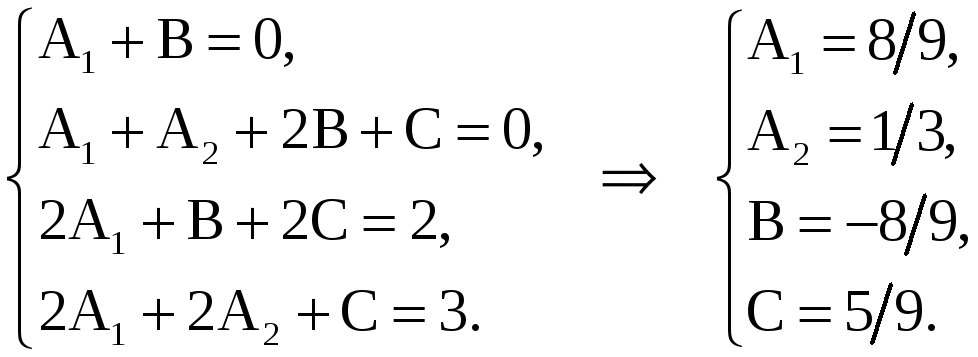
Таким образом,
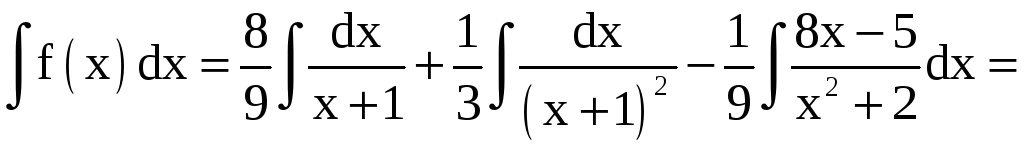

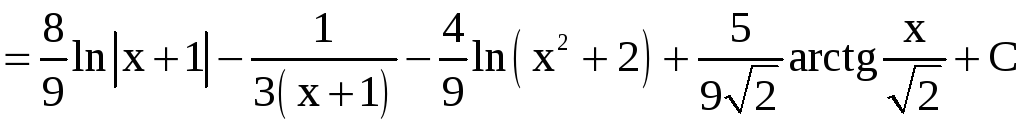 .
.
б)
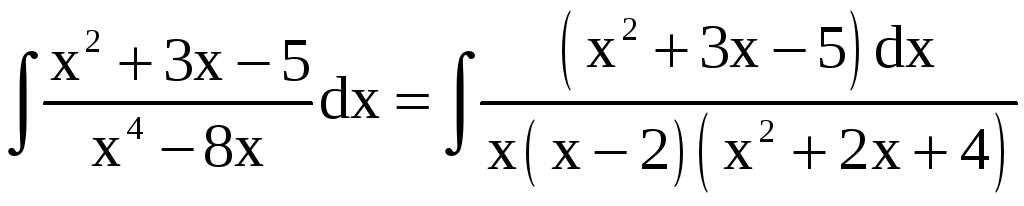 .
.
Разложим
подынтегральную функцию
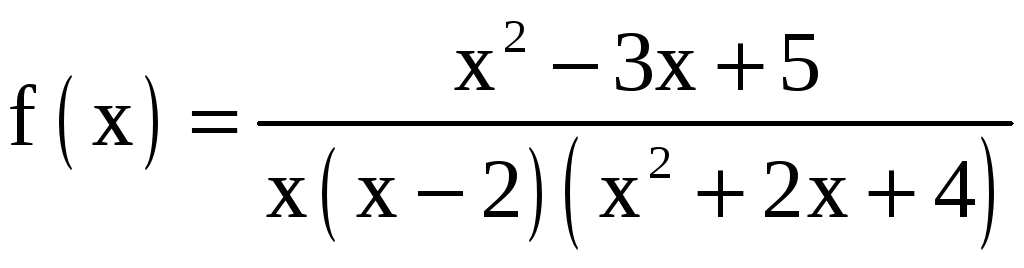 на сумму простых дробей:
на сумму простых дробей:
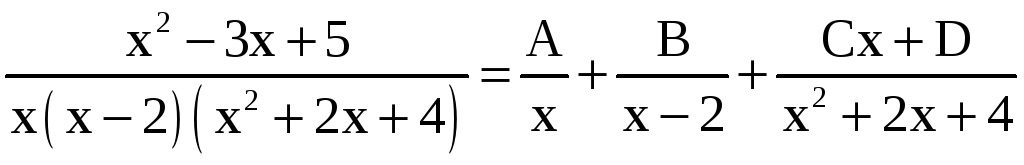 ;
;
![]()
![]() . (1)
. (1)
x = 0; –8A = +5. A = –5/8,
x = 2; 24B = 3. B = 1/8.
Из равенства (1) следует (приравниваются коэффициенты при x3 и x):
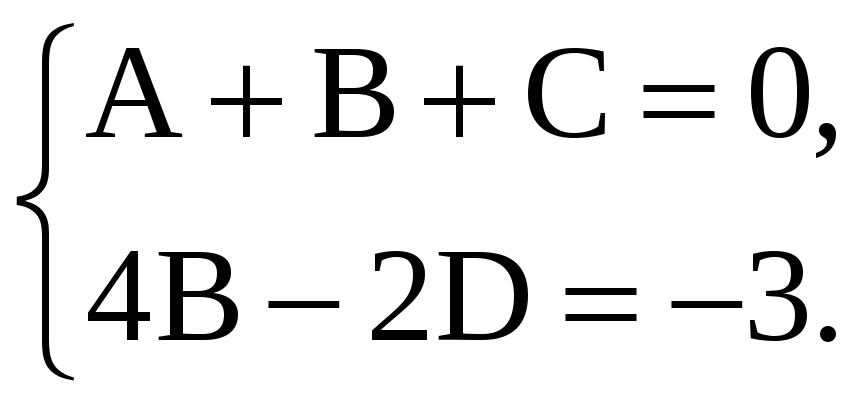
Отсюда, зная уже
A = –5/8 , B = 1/8, находим C = 1/2, D = 7/4. Таким
образом,
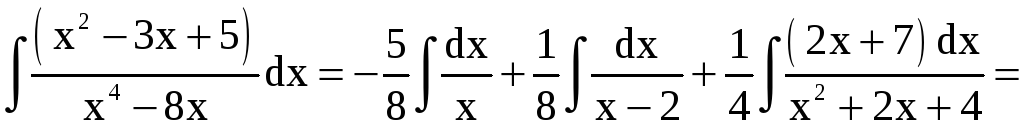
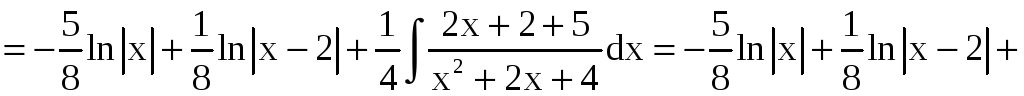
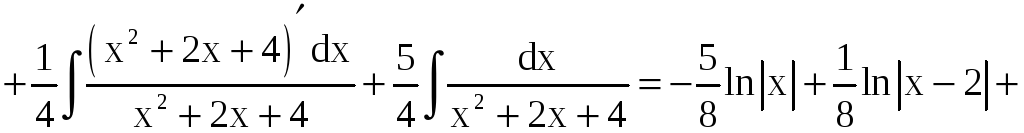
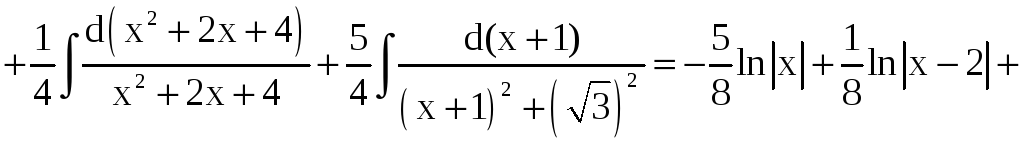
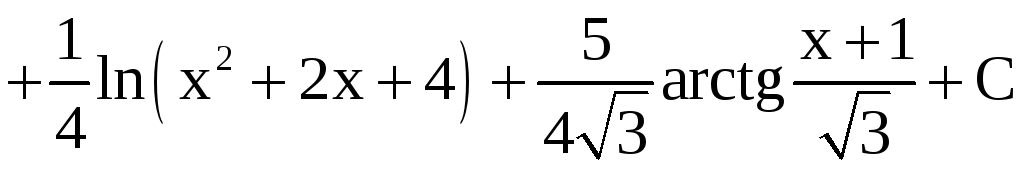 .
.
в) Рациональная
функция
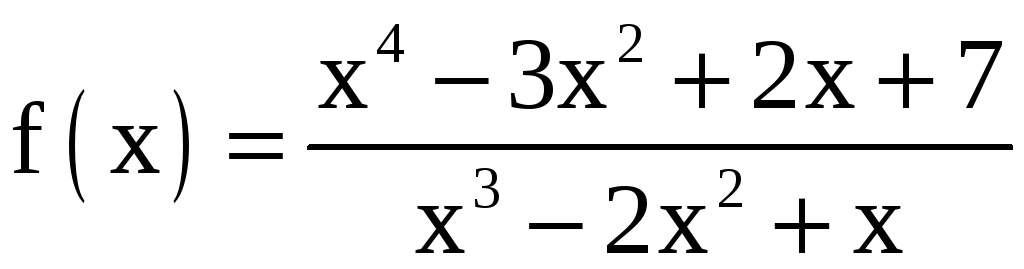 представляет собой неправильную дробь.
Выделим целую часть делением уголком
представляет собой неправильную дробь.
Выделим целую часть делением уголком
 x4
– 3x2
+ 2x +7 x3
– 2x2
+ x
x4
– 3x2
+ 2x +7 x3
– 2x2
+ x
 x4
– 2x3
+ x2
x + 2
x4
– 2x3
+ x2
x + 2
 2x3
– 4x2
+ 2x + 7
2x3
– 4x2
+ 2x + 7
2x3 – 4x2+2x
7
Таким образом,
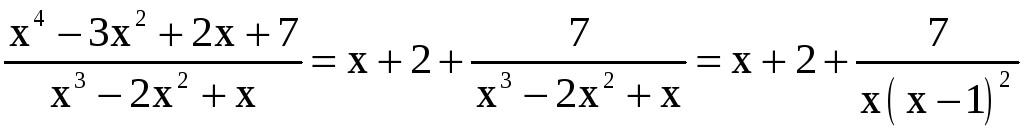 .
.
Разложим правильную
дробь
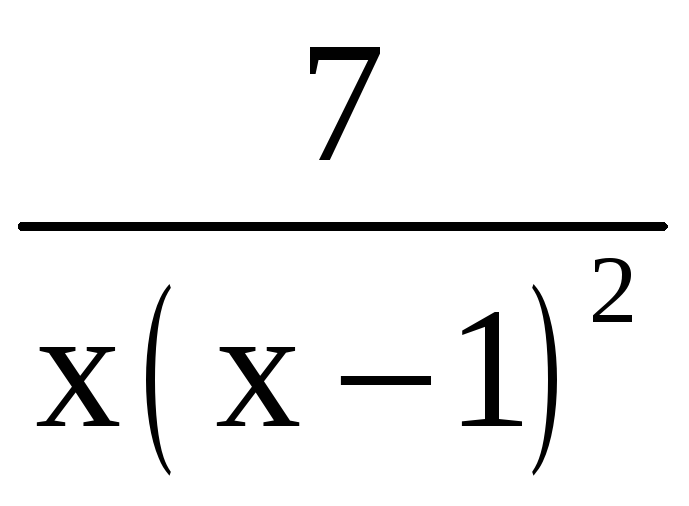 на сумму простых дробей:
на сумму простых дробей:
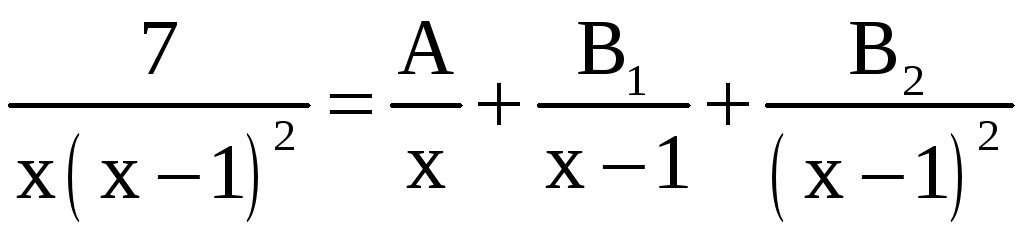 ;
;
![]() ; (2)
; (2)
x = 0; A = 7;
x = 1; B2 = 7.
Сравнивая старшие коэффициенты в обеих частях равенства (2), находим A + B1 = 0, B1 = –A = –7 . Таким образом,
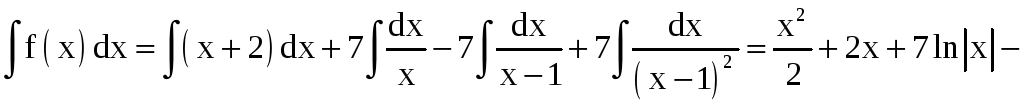
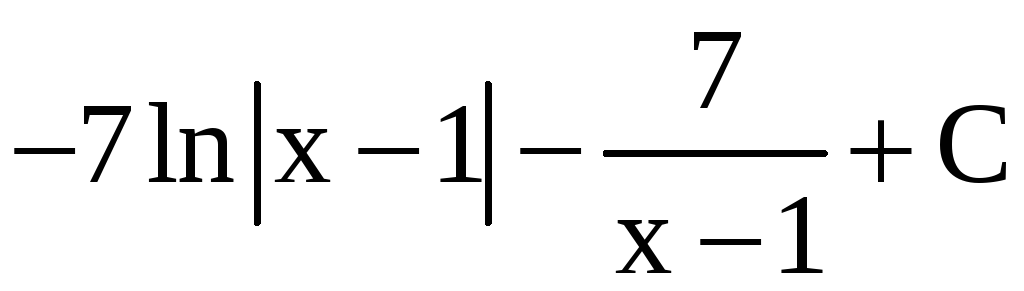 .
.