Оценка степени монопольной власти (индекс Лернера) (расчетный пример)

Действующая в условиях несовершенной конкуренции фирма имеет функцию предельной выручки . При этом зависимость общих издержек от объема выпуска описывается функцией . Какой степенью рыночной власти обладает фирма?

Решение.

Оценим степень монопольной власти фирмы с помощью индекса Лернера: . Для этого определим устанавливаемую монополистом цену и соответствующую ей величину предельных затрат .

Прибыль фирмы-монополиста максимизируется при , где . Следовательно, ; ; .

Для линейной кривой предельного дохода вида функция спроса имеет вид , т.е. .

Величину предельных издержек определим из рассчитанной ранее функции: .

Тогда индекс Лернера равен .

Ответ: .

Максимизация прибыли монополистом, осуществляющим ценовую дискриминацию третьей степени (расчетный пример)

Монополия, максимизирующая прибыль, может продавать продукцию на двух сегментах рынка, имеющих следующие функции спроса и . Функция общих затрат монополии имеет вид: ; . Какие цены получит монополия при проведении ценовой дискриминации и каким будет объем продаж на каждом сегменте рынка?

Решение.

Условие максимизации прибыли фирмы-монополиста, осуществляющей ценовую дискриминацию, в данном случае можно записать следующим образом: ; . Рассчитаем соответствующие функции.

есть первая производная функции : .

Для нахождения функций используем формулу , где a и b – коэффициенты в обратных линейных функций спроса вида . Для этого выразим функции спроса в виде обратных:

; ; ;

; ; .

Тогда соответствующие функции можно представить как: ; .

Равновесные объемы по сегментам и для рынка в целом находим из решения системы следующих уравнений:

;

;

.

Следовательно, .

Тогда,

;

;

; .

.

Цены по сегментам определяем из обратных функций спроса:

;

.

Ответ: , ; , .

Максимизация прибыли монополиста с несколькими заводами (расчетный пример)

Некоторая монополия имеет кривую спроса, заданную уравнением . Кривые валовых издержек для двух его предприятий имеют вид: , соответственно. Сколько продукции должен выпускать монополист, и как эту продукцию следует распределить между двумя предприятиями, чтобы получить максимальную прибыль?

Решение.

Условие максимизации прибыли фирмы-монополиста с несколькими заводами можно представить как ; . Рассчитаем соответствующие функции.

Для нахождения функции используем формулу , где a и b – коэффициенты в обратной линейной функции спроса вида , т.е. .

Функции определим, как первые производные от функций :

; .

Равновесные объемы по каждому заводу и фирмы в целом находим из решения системы следующих уравнений:

;

;

.

Выразим величину из первого уравнения и подставим ее во второе уравнение:

;

; ;

; ; ;

.

Тогда, .

Общий объем выпуска монополиста составит: .

Ответ: ; ; .

Максимизация прибыли в модели дуополии Курно (расчетный пример)

Спрос в отрасли описывается функцией . В отрасли присутствуют две фирмы, которые взаимодействуют по Курно. Предельные затраты обеих фирм одинаковы и равны 20. Постоянные издержки равны нулю. Определите:

1. объем выпуска каждой фирмы, максимизирующий ее прибыль, и рыночную цену на продукцию;

2. уровень выпуска и цену, обеспечивающие максимальную прибыль фирмам в случае, если они образуют картель.

Решение.

1) Представим функцию спроса в виде обратной: ; ; . Тогда функция остаточного спроса для первого дуополиста имеет вид .

Т.к. , а , то .

Выразим функции реакции для дуополистов. Прибыль первого дуополиста достигает максимума при . Поэтому его функция реакции имеет вид: . Предполагая (т.к. не указано иное), что фирмы являются идентичными, функцию реакции второго дуополиста можно выразить как .

Т.к. в модели Курно фирмы ведут себя как равноправные конкуренты, то равновесные рыночные показатели можно определить из решения следующей системы уравнений:

;

; ; ;

;

.

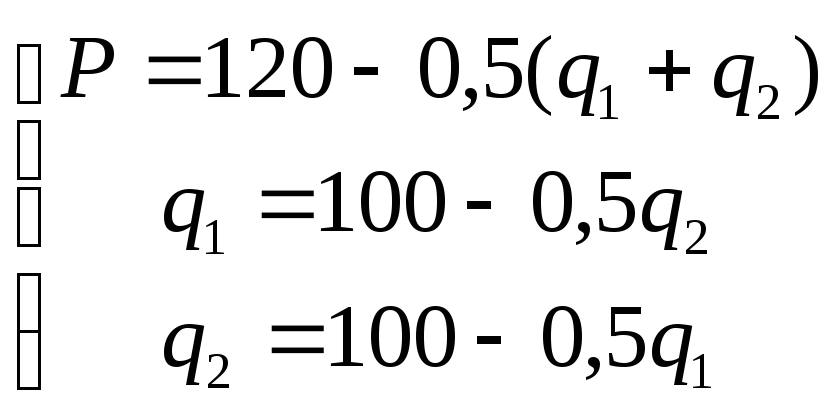2) При образовании картеля таковой ведет себя на рынке как монополист. Следовательно, правило максимизации прибыли имеет вид .

Для линейной обратной функции спроса вида функция имеет вид : ; . по условию.

Приравняв, получаем: ; ; ; .

Ответ: 1) ; ; 2) ; .