
- •Элементы и функциональные устройства судовой автоматики
- •Керчь, 2006
- •Введение
- •Функциональная связь
- •Примеры объединения элементов в группы типовых звеньев
- •3. Элементы с непосредственным преобразованием
- •4. Элементы с промежуточным преобразованием
- •5. Согласование характеристик и основные параметры элементов с промежуточными преобразованиями
- •6. Схемы формирования сигналов
- •7. Понятия надежности элементов автоматики
- •8. Датчики перемещения
- •9. Функциональные потенциометры
- •10. Датчики величины усилия
- •11. Датчики скорости
- •12. Датчики скорости с изменяющейся эдс
- •13. Асинхронный тахогенератор (атг)
- •Понятие о магнитных усилителях (му)
- •Электромашинный усилитель с поперечным полем (эму с пп)
- •Выбор эму
- •Электромашинный усилитель с поперечным полем (эму с пп)
- •Выбор эму
- •Датчики угла рассогласования
- •Сельсин
- •Исполнительные элементы
- •Шаговые двигатели
- •Двухфазный магнитоэлектрический шаговый двигатель
- •Электромагнитные элементы.
- •Нейтральное реле постоянного тока
- •Нейтральное реле постоянного тока состоит:
- •Тяговые и механические характаристики реле
- •Параметры реле
- •Схемные способы
- •Поляризованное реле постоянного тока
- •98309 Г. Керчь, Орджоникидзе, 82.
-
Примеры объединения элементов в группы типовых звеньев
Все элементы автономических систем в зависимости от их характеристик в установившихся и переходных режимах можно разделить на определенные группы простейших звеньев.
-
идеальные (безынерционные) звенья
Уравнение динамики идеального звена имеет вид
Хвык(t) = r Xвх(t) (1)
В оперативной форме
Хвык(р) = r Xвх(р) (2)
Передаточная функция идеального звена
W(p)
=
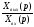 = r (3)
= r (3)
Примерами конструктивного выполнения идеального звена могут быть:
-
жесткий механический рычаг;
-
механический редуктор;
-
потенциометр;
-
электронная усилительная лампа;
-
полупроводниковый триод и др., если уравнения их динамики можно представить уравнением (1).
инерционное (апериодическое) звено первого порядка
Уравнение динамики инерционного звена первого порядка имеет вид
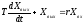 ,
(4)
,
(4)
где T – постоянная времени, обусловленная наличием массы, момента инерции, индуктивности, емкости и т.д.;
r – коэффициент усиления (или передачи).
Оперативное уравнение
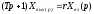 ,
(5)
,
(5)
Передаточная функция
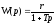 ,
(6)
,
(6)
Примерами инерционного звена первого порядка являются:
-
пассивные четырехполюсники, состоящие из сопротивления и индуктивности или из сопротивления и емкости;
-
термопара, а также (при определенных допущениях) магнитный усилитель;
-
генераторы постоянного и переменного тока;
-
электрические двигатели (если вход – ток якоря, а выход – угловая скорость) и т.д., если уравнения их динамики можно представить в виде (4).
-
интегрирующее звено
Уравнение динамики:
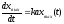
 (7)
(7)
или

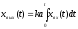
Где ka – коэффициент пропорциональности.
Операционное уравнение
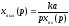 (8)
(8)
Передаточная функция
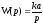 (9)
(9)
Примерами интегрирующего звена являются:
-
электрический двигатель при пренебрежении электрической постоянной времени (если вход – напряжение питания, а выход – угол поворота ротора или якоря);
-
поршневой гидравлический сервомотор при пренебрежении массой и силами трения (если вход – скорость подачи жидкости в цилиндр или открытие золотника, а выход – перемещение поршня) и т. д., если уравнения их динамики имеют вид уравнения(7).
г) инерционные звенья второго порядка
Уравнение динамики инерционного звена второго порядка имеют вид:
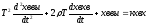 ,
(10)
,
(10)
где Т – постоянная времени;
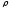 - коэффициент
демпфирования;
- коэффициент
демпфирования;
к - коэффициент усиления (или передачи).
В операторной форме:
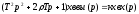 (11)
(11)
Передаточная функция:
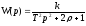 (12)
(12)
Примерами выполнения инерционных звеньев второго порядка могут быть:
-
центробежный маятник;
-
контур содержащий R, L и C;
-
ЭМУ поперечного поля;
-
электродвигатель постоянного тока (если входом является напряжение якорной цепи, а выходом – скорость вращения при учете постоянной времени цепи якоря и электромеханической постоянной времени) и т. д., если уравнения их динамики можно представить в виде уравнения (10).
д) консервативное звено
Уравнение динамики:
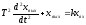 (13)
(13)
Это частный случай звена второго порядка, когда отсутствует демпфирование (ρ=0)
Передаточная функция:
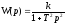 (14)
(14)
Примером консервативного звена может быть идеальный пассивный четырехполюсник, состоящий из L и C и другие элементы, если уравнения их динамики имеет вид уравнения (13).
е) дифференцирующие звенья
Уравнения динамики:
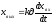 (идеальное диф. звено)
(15)
(идеальное диф. звено)
(15)
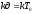 -
эквивалентный коэффициент усиления
-
эквивалентный коэффициент усиления
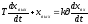 (реальное диф.
звено без статизма) (16)
(реальное диф.
звено без статизма) (16)
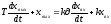 (реальное диф.
звено со статизмом), (17)
(реальное диф.
звено со статизмом), (17)
если
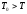 или
ПИД (пропор. диф.)
или
ПИД (пропор. диф.)
Примерами могут быть:
-
Электрические цепи содержащие L и C;
-
Демпфер с пружиной
-
Тахогенератор, и др. если уравнения динамики имеют вид уравнений(15,16,17).
