03 семестр / Разное / Пример курсача / теория

Задача о движении частицы в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Собственные функции и спектр энергий частицы. Плотность вероятности. Вероятность нахождения частицы в заданной области пространства.

Рассмотрим движение частицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками.

З

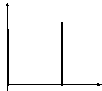
U(x)

I II III

0 d x

Рис.1

ависимость потенциальной энергии описывается так:

Всю область изменения переменной x разобьем на три области (рисунок 1). По условию задачи электрон находится в области II. Поскольку потенциальная яма имеет, бесконечно высокие стенки, то электрон не может выйти за ее пределы, т.е. вероятность обнаружить электрон в областях I и III равна нулю,

(1)

следовательно и Ψ(x) = 0.

И

(2)

з условия непрерывности Ψ функции, запишем граничные условия

(3)

З

(4)

апишем уравнение Шредингера в общем виде для одномерного случая

У

(5)

равнение Шредингера для движения электрона вдоль оси х для области II принимает вид:

Уравнение (2) соответствует движению свободной частицы, т.к. в области 0 < x <d потенциальное поле U(х) = 0.

В

(6)

ведем обозначение

С учетом (6) уравнение (5) запишем в виде:

(7)

У

(8)

равнение (7) имеет решение:

Постоянные A, d и k мы найдем из условий непрерывности волновой функции и нормировки. На левой границе, из условия (2)

следует , что d=0.

Н

(9)

а правой границе, из условия (3)

следует , что

kd = πn,

где n – натуральные числа. Нулевое значение n в ряд допустимых значений не входит, т.к. иначе волновая функция везде бы обращалась в ноль.

Состояние с минимальной энергией (n = 1) называют основным, остальные (n≥0) - возбужденными.

Р

(10)

ешения уравнения (4) в виде

Отвечающие собственным значениям энергии частицы Е_n, являются

с

(11)

обственными функциями. Их можно записать с учётом (4) в виде

Постоянную А найдём из условия нормировки Ψ- функции:

(12)

так как , то

Учитывая (5), будем иметь

;

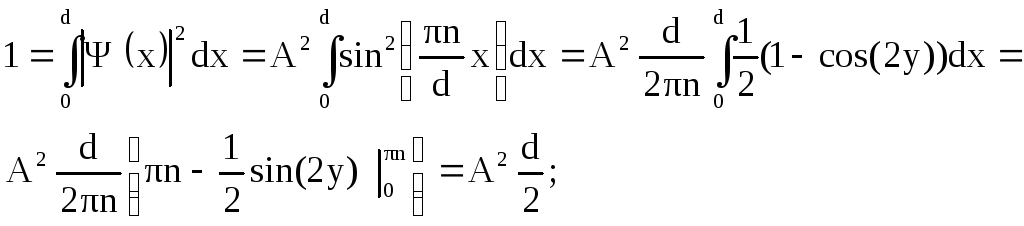
(13)

О

(14)

кончательный вид волновой функции

Из соотношений (6) и (9) находим собственные значения энергии

электрона:

(15)

   

Возможны только такие состояния, для которых E принимает одно из дискретных значений то есть частица, “запертая” в потенциальной яме, может иметь только дискретный спектр энергий. Введенное выше число n, определяющее значение энергии электрона, называют квантовым числом, квантованные значения E_n называются энергиями квантовых состояний.

Говорят, что частица находится в квантовом состоянии n, если ее движение описывается волновой функцией Ψ_n(x).

Три первых уровня энергии, соответствующие им волновые функции Ψ(x) и квадраты волновых функций изображены на рисунке 2.

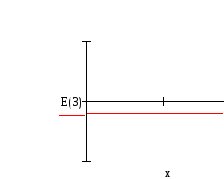
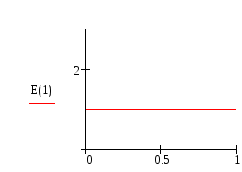
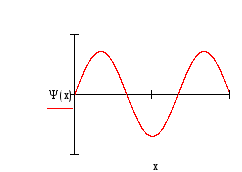
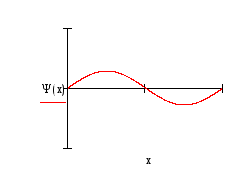
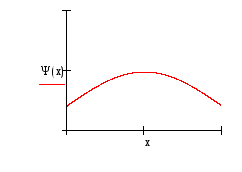
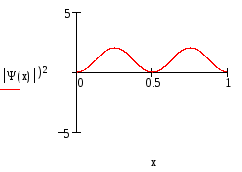
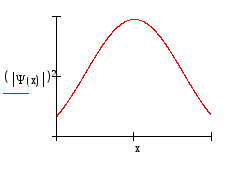
Рис.2

Р

аспределение вероятности обнаружения электрона в том или ином месте внутри ямы при различных значениях энергии электрона находим из формулы

Это распределение неоднородно и зависит от n. Чем больше n, тем сильнее неоднородность. При очень больших значениях квантового числа (большие возбуждения) дискретность состояний перестает проявляться. Фактически наблюдаем переход к непрерывному изменению энергии.

5