
- •1 Курс, 1 семестр.
- •1.Свойства степени с произвольным показателем.
- •2. Определение логарифма числа и его свойства. Натуральные и десятичные логарифмы.
- •Свойства логарифмов.
- •3.Тригонометрические функции числового аргумента(определения, табличные значения).
- •Табличные значения тригонометрических функций
- •1.Арккосинус
- •Табличные значения арккосинуса
- •2.Арксинус
- •Табличные значения арксинуса
- •3.Арктангенс
- •Табличные значения арктангенса
- •4.Арккотангенс
- •5.2.Формулы суммы и разности аргументов.
- •5.3.Формулы двойного аргумента.
- •5.4.Вывод формул понижения степени.
- •10. Степенная функция.
- •Показатель степени k2nчётное натуральное число.
- •Показатель степени k2n1 нечётное натуральное число.
- •Показатель степени k-2n, где nнатуральное число.
- •Показатель степени k(2n1), где nнатуральное число.
- •Показатель степени k-положительное действительное нецелое число.
- •Показатель степени k-отрицательное действительное нецелое число.
- •11. Показательная функция.
- •Свойства:
- •12. Логарифмическая функция.
-
Показатель степени k-положительное действительное нецелое число.
Областью
определения такой функции являются
неотрицательные числа x 0,
множеством значений-неотрицательные
числа y
0,
множеством значений-неотрицательные
числа y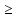 0;
функция-возрастающая на промежутке
x
0;
функция-возрастающая на промежутке
x 0.
0.
На
рисунке 5(а) представлены графики функций
y=x1/2и
y=x1/3(показатель
k 1),
на рисунке 5(б)-графики функций y=x2/3
и y=x4/3(показатель
k
1),
на рисунке 5(б)-графики функций y=x2/3
и y=x4/3(показатель
k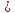 1)
1)
Y
y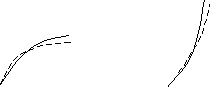
Y=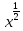 Y=
Y=
Y=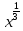 Y=
Y=
0 x 0 x
1 1
Рисунок 5(а) Рисунок 5(б)
-
Показатель степени k-отрицательное действительное нецелое число.
Такая
функция обладает следующими свойствами:
область определения-положительные
числа y 0;
множество значений-положительные числа
y
0;
множество значений-положительные числа
y 0;
функция-убывающая на промежутке x
0;
функция-убывающая на промежутке x 0/
0/
Этот
случай проиллюстрирован графиками на
рисунке 6: y=x-1/2= и y=x-1/3=
и y=x-1/3=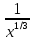 .
.
На
рисунке 7 в I
квадранте представлены кривые,
соответствующие функциям y=xk
при k 0,
на графиках рисунка 8 при k
0,
на графиках рисунка 8 при k
-2
-1

-10
2
3

10
y
Рис.6
Y
Рис.7 y
Рис.8





-0,1
y ;k
;k 0
0

-0,1
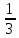
y= 1
1
1
1




 1
1

0,1
1
y=
x
x
-2
-10
y ;k
;k 0
0
x
0 1 0 1 0 1
11. Показательная функция.
Определение: Функция вида y=ax, где a положительное и не равно единице, называется показательной функцией.
y=ax 2 случая
x
x
1)
0 a
a 1
Пример: y=
1
Пример: y= 2)
а
2)
а 0
Пример: y=2x
0
Пример: y=2x
X 0 1 2 -1 -2 X 0 1 2 -1 -2
y
1
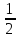
 2 4
y
1
2 4
y
1

 2 4
2 4
y y






x
y= y=2x
y=2x




 Экспонента
Экспонента
 Экспонента
Экспонента








1




x x
-2 -1 1 2 -2 -1 1 2
Точно также будет выглядеть график Точно также будет выглядеть график любой
любой
функции вида y=ax,
при 0 a
a 1
любой функции y=ax,
при условии, что a
1
любой функции y=ax,
при условии, что a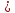 1
1
