
- •1 Курс, 1 семестр.
- •1.Свойства степени с произвольным показателем.
- •2. Определение логарифма числа и его свойства. Натуральные и десятичные логарифмы.
- •Свойства логарифмов.
- •3.Тригонометрические функции числового аргумента(определения, табличные значения).
- •Табличные значения тригонометрических функций
- •1.Арккосинус
- •Табличные значения арккосинуса
- •2.Арксинус
- •Табличные значения арксинуса
- •3.Арктангенс
- •Табличные значения арктангенса
- •4.Арккотангенс
- •5.2.Формулы суммы и разности аргументов.
- •5.3.Формулы двойного аргумента.
- •5.4.Вывод формул понижения степени.
- •10. Степенная функция.
- •Показатель степени k2nчётное натуральное число.
- •Показатель степени k2n1 нечётное натуральное число.
- •Показатель степени k-2n, где nнатуральное число.
- •Показатель степени k(2n1), где nнатуральное число.
- •Показатель степени k-положительное действительное нецелое число.
- •Показатель степени k-отрицательное действительное нецелое число.
- •11. Показательная функция.
- •Свойства:
- •12. Логарифмическая функция.
10. Степенная функция.
Функция
вида y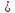 xk,
где k
xk,
где k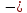 действительное
число, называется степенной
функцией
с показателем k.
действительное
число, называется степенной
функцией
с показателем k.
Свойства и график степенной функции существенным образом зависят от показателя k. Рассмотрим различные возможные варианты.
-
Показатель степени k2nчётное натуральное число.
В этом
случае областью определения функции
y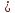 x2n
является множество R
всех действительных чисел; множество
значений
x2n
является множество R
всех действительных чисел; множество
значений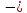 неотрицательные
числа (y
неотрицательные
числа (y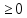 );
функция является чётной ((-x)2n
);
функция является чётной ((-x)2n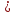 x2n);
функция убывающая на промежутке x
x2n);
функция убывающая на промежутке x
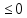 и возрастающая на промежутке x
и возрастающая на промежутке x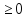 .
.
На
рисунке 1 приведены графики функции
y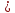 x2
и y
x2
и y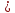 x4.
x4.
y
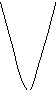
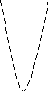
y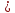 x4
x4
y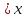 2
2
x Рисунок 1
-
Показатель степени k2n1 нечётное натуральное число.
Такая
степенная функция y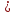 x2n-1,
где n
x2n-1,
где n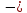 натуральное
число, обладает следующими свойствами:
область определения
натуральное
число, обладает следующими свойствами:
область определения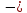 множество
R,
множество значений
множество
R,
множество значений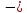 множество
R,
функция
является нечётной, так как (
множество
R,
функция
является нечётной, так как (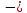 x)2n-1
x)2n-1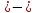 x2n
x2n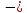 1;
функция
1;
функция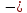 на
всей действительной оси.
на
всей действительной оси.
Графики,
изображённые на рисунке 2, соответствует
функциям y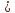 x3
и y
x3
и y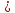 x5.
x5.
(Отметим, что в частном случае при n=1 получаем функцию y=x с графиком биссектрисы первого и третьего квадрантов.)
Y
y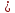 x3
x3
x
y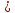 x5
x5
Рисунок 2
-
Показатель степени k-2n, где nнатуральное число.
В этом
случае областью определения функции
y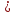 x-2
x-2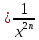 является множество R,
кроме x
является множество R,
кроме x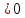 ;
множеством значений-положительные
числа y
;
множеством значений-положительные
числа y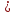 0;
функция является чётной, так как
0;
функция является чётной, так как
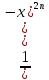 ;
функция возрастающая на промежутке x
;
функция возрастающая на промежутке x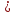 0
и убывающая на промежутке x
0
и убывающая на промежутке x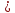 0.
0.
На
рисунке 3 представлены графики функции
y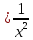 и y
и y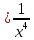 .
.
Y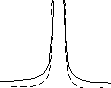
y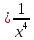
y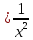
-
x
-1 1
Рисунок 3
-
Показатель степени k(2n1), где nнатуральное число.
Областью
определения такой функции y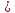 x-(2n-1)
x-(2n-1)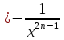 является множество R,
кроме x
является множество R,
кроме x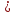 0;
множеством её значений-множество R,
кроме y=0;
функция является убывающей на промежутке
x
0;
множеством её значений-множество R,
кроме y=0;
функция является убывающей на промежутке
x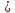 0,
x
0,
x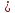 0.
0.
На
рисунке 4 приведены графики функций y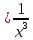 и y
и y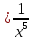
y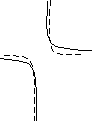
y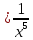
y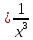
-
x
Рисунок 4
