
- •1 Курс, 1 семестр.
- •1.Свойства степени с произвольным показателем.
- •2. Определение логарифма числа и его свойства. Натуральные и десятичные логарифмы.
- •Свойства логарифмов.
- •3.Тригонометрические функции числового аргумента(определения, табличные значения).
- •Табличные значения тригонометрических функций
- •1.Арккосинус
- •Табличные значения арккосинуса
- •2.Арксинус
- •Табличные значения арксинуса
- •3.Арктангенс
- •Табличные значения арктангенса
- •4.Арккотангенс
- •5.2.Формулы суммы и разности аргументов.
- •5.3.Формулы двойного аргумента.
- •5.4.Вывод формул понижения степени.
- •10. Степенная функция.
- •Показатель степени k2nчётное натуральное число.
- •Показатель степени k2n1 нечётное натуральное число.
- •Показатель степени k-2n, где nнатуральное число.
- •Показатель степени k(2n1), где nнатуральное число.
- •Показатель степени k-положительное действительное нецелое число.
- •Показатель степени k-отрицательное действительное нецелое число.
- •11. Показательная функция.
- •Свойства:
- •12. Логарифмическая функция.
Экзаменационные вопросы по курсу «Математика»
1 Курс, 1 семестр.
1.Свойства степени с произвольным показателем.
a) Степень с натуральным показателем.
Определение:
 ,
где n-любое
натуральное число называется степенью
с натуральным показателем.
,
где n-любое
натуральное число называется степенью
с натуральным показателем.
 =a·a·a…·a
=a·a·a…·a
n-раз
 =2·2·2·2=4·4=16
=2·2·2·2=4·4=16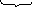
4 раза
a- основание степени
т-показатель степени
 = a
5)
= a
5)
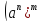 =
=

 = 1
6)
= 1
6)
 =
=
 ·
·

n
3)
 ·
· =
=
 7)
7)
 =
=

4)
 =
=
 8)
8)
 =
=

б) Степень с рациональным показателем.
Определение:
Под степенью с рациональным показателем
 ,
где q
,
где q 1
понимают
1
понимают
 ,
т.е.
,
т.е.
 =
=
 ,
a>0
,
a>0
 =
=

Все свойства степени с натуральным показателем верны для степени с любым рациональным показателем и положительным основанием.
r
и s
–рациональные числа, т.е. числа вида
 q
q 1
1
s
1)
 = a 4)
= a 4)
 =
=
 7)
7) =
=

2)
 = 1 5)
= 1 5) =
=
 8)
8)
 =
=
3)
 ·
· =
=

 =
=
 ·
·
 9)
9)
 =
=

2. Определение логарифма числа и его свойства. Натуральные и десятичные логарифмы.
Показательное
уравнение вида
 =b
(при условии, что числа a
и b
положительны, где a
=b
(при условии, что числа a
и b
положительны, где a 0
; a
0
; a 0
и b
0
и b 0)
имеет решение, которое можно записать:
0)
имеет решение, которое можно записать:

|
- Основное логарифмическое тождество.
|
Например,
 =
7;
=
7;

 ;
;
 125 и т.д.
125 и т.д.
Определение:
Логарифмом положительного числа b
по положительному и отличному от единицы
основанию a,
называется показатель степени x,
в которую нужно возвести число a,
чтобы получить число b.
Таким образом,
 =x
=x
 b
; a
> 0 ; a
< 0 и a
b
; a
> 0 ; a
< 0 и a 1
1
Операцию нахождение логарифма называют логарифмированием. Эта операция является обратной по отношению к операции возведение в степень соответствующим основаниям.
Возведение в степень Логарифмирование
 =25
=25
 =2
=2
 =0,001
=0,001
 =3
=3
Определение:
Логарифмом по основанию 10 называется
десятичным
логарифмом и обозначается символом lg
(читается десятичный логарифм), т.е.
вместо
 пишут lg
5. Если в основании логарифма стоит число
a
= e
пишут lg
5. Если в основании логарифма стоит число
a
= e 2,71828…
e
2,71828…
e 2,7,
то такой логарифм называется
натуральным
и обозначается символом:
2,7,
то такой логарифм называется
натуральным
и обозначается символом:
 (читается
натуральный логарифм), т.е. вместо записи
логарифм трёх по основанию e
пишут
(читается
натуральный логарифм), т.е. вместо записи
логарифм трёх по основанию e
пишут
 =ln3
=ln3
Особо выделим 3 формулы:
1) =1
(
=1
( =1)
=1)
2) =0
(
=0
( =0)
=0)
3) =r
(
=r
( =2)
=2)

 =
b
=
b