8. Условная вероятность. Независимость событий

 

Условная вероятность. Независимые и зависимые события.

Вероятность появления события  А  при условии, что событие  В  произошло, называется  условной вероятностью события  А  и вычисляется по формуле:

          

События  А , В  Е называются независимыми, если  Р ( А  В ) = Р ( А ) · Р ( В ) .

В противном случае события  А и В называются зависимыми.

9.Вероятность «хотя бы одного» события

Хотя бы одно это противоположное событие тому, что ни одного. Если р вероятность того, что событие произойдёт, а n – количество событий, то Р=1-(1-р)^n.

10.Формула полной вероятности

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

11. Формула Байеса

Формула Байеса:,

P(A) — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

P(A | B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность);

P(B | A) — вероятность наступления события B при истинности гипотезы A;

P(B) — вероятность наступления события B.

12. Повторные независимые испытания. Формула Бернулли

Примеры повторных испытаний:

1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;

2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. , а вероятность противоположного события (событие А не наступило) - буквой .

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

13.Муавра-Лапласа

Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n) значению функции:

при x=(k-np)/√npq

Итак, вероятность того, что событие А появится в n независимых испытаниях ровно k раз, приближенно равна , где x=(k-np)/√npq

Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний . При больших значениях пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.

Теорема. Если вероятность  наступления события  в каждом испытании постоянна и мала, а число независимых испытаний  достаточно велико, то вероятность наступления события  ровно  раз приближенно равна

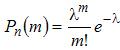,(3.4)

где .

14.Интегральная теорема Лапласа. Имеет место следующее утверждение.     Теорема. Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна . Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная

величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np, .