6. Постоянный электрический ток

6.1 Законы постоянного тока. Законы Ома, закон Джоуля – Ленца

Задачи этого раздела посвящены применению законов постоянного электрического тока к расчету электрических цепей. Для решения этих задач используются законы Ома для однородного участка цепи, закон Ома для замкнутой цепи и закон Джоуля – Ленца.

Электрическим током называют упорядоченное движение заряженных частиц. За направление тока принимают направление движения положительно заряженных частиц.

Количественной характеристикой электрического тока является - сила тока.

Сила тока - скалярная физическая величина, численно равная заряду, прошедшему через поперечное сечение проводника в единицу времени

.

При неравномерном распределении тока по поверхности, через которую переносится заряд, вводится векторная характеристика – плотность тока.

Плотность тока - векторная величина. Её модуль численно равен величине заряда, протекающего через единицу поперечного сечения проводника за единицу времени. Направление вектора в каждой точке проводника совпадает с направлением тока, т.е. с направлением скорости упорядоченного движения положительных зарядов на данном участке проводника.

,

где dI – сила тока, протекающего в данном месте внутри проводника через элементарную площадку dS, расположенную перпендикулярно к направлению тока.

Используя вектор плотности тока, можно найти силу тока, протекающего через любую поверхность S :

,

где - угол между вектором и вектором нормали к элементарной площадке.

Электрический ток существует при наличии свободных зарядов и электрического поля. Такие условия можно создать в различных средах: в твердых телах, жидкостях газах и в вакууме. В различных средах носителями заряда являются различные частицы. В металлах ток проводимости обусловлен движением электронов.

В начале 19^го века Г.Ом экспериментально установил закон:

Сила тока , текущего по однородному участку цепи, прямо пропорциональна напряжению , приложенному к этому участку, и обратно пропорциональна сопротивлению этого участка .

.

Однородным участком электрической цепи называют участок, на котором направленное движение зарядов происходит только под действием кулоновских сил, т.е. участок не содержит источника тока. Для такого участка напряжение совпадает с разностью потенциалов между начальной и конечной точками участка цепи .

Коэффициент пропорциональности в законе Ома называется электрической проводимостью участка цепи, а величина обратная проводимости называется электрическим сопротивлением.

Сопротивление участка проводника зависит от его размеров и формы, материала и физических условий (температуры и др.). Для цилиндрического проводника длиной и площадью поперечного сечения сопротивление можно вычислить по формуле ,

где r - удельное сопротивление материала проводника, l - длина проводника, S - площадь поперечного сечения проводника. Удельное сопротивление зависит от температуры следующим образом

r = r₀ (1 + at),

где r₀ - удельное сопротивление материала проводника при 0^оС. Его численное значение можно взять из справочников или оно приводится в задаче. Величина обратная удельному сопротивлению называется удельной проводимостью.

a - температурный коэффициент сопротивления, который численно равен относительному изменению удельного сопротивления при изменении температуры на один градус.

- определение температурного коэффициента сопротивления. Расчет сопротивления участка цепи при параллельном и последовательном соединении отдельных проводников

; R = R₁ + R₂ + …

(параллельное соединение) (последовательное соединение)

Закон Ома в дифференциальной форме

,

где - плотность тока на данном участке цепи;

σ - удельная проводимость проводника;

r - удельное сопротивление проводника;

- напряженность электрического поля внутри проводника.

Закон Ома для неоднородного участка цепи ( участок содержит ЭДС):

.

а) j₁>j₂ и j₊ > j_-- В этом случае j₁ - j₂ =IR + e

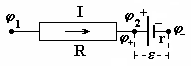или U = (j₁ -j₂) - e

б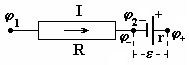) j₁ > j₂ и > j_- < j_+, тогда j₁ -j₂ =IR - e. При таком включении ЭДС падение напряжения на всем участке

U = (j₁ - j₂) + e.

Закон Ома для полной (или замкнутой) цепи: ток в цепи прямо пропорционален ЭДС и обратно пропорционален полному сопротивлению цепи

,

где - ЭДС источника тока;

R - сопротивление внешнего участка цепи;

r - внутреннее сопротивление источника тока.

При протекании электрического тока по проводнику в проводнике выделяется некоторое количество теплоты Q. При протекании тока по однородному участку цепи работа сил электрического поля по перемещению заряда в проводнике вся расходуется на выделение тепла, поэтому количество выделившегося тепла равняется работе сил электрического поля:

.

Мощность тока равна

Закон Джоуля – Ленца в дифференциальной форме:

,

где – объёмная плотность тепловой мощности, т.е. количество теплоты, которое выделяется в единице объема проводника в единицу времени.

Закон Фарадея для электролиза

,

где k - электрохимический эквивалент вещества.

КПД электрической цепи

,

где А_n -полезная работа тока на внешнем участке цепи ,

А₃ – работа затраченная равная полной энергии, вырабатываемой источником тока ,

где R- сопротивление нагрузки, а r – внутреннее сопротивление источника тока.

Плотность тока , средняя скорость <> упорядоченного движения носителей заряда в проводниках и их концентрация n связаны соотношением

,

где e – элементарный заряд.

Удельная проводимость , средняя длина свободного пробега <> и средняя скорость хаотического теплового движения электронов u связаны соотношением

,

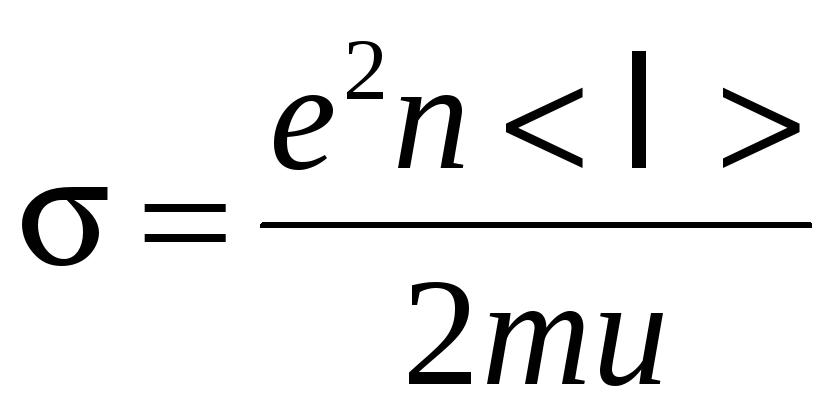где e и m – заряд и масса электрона, n – концентрация электронов.