4. Специальные графы

Граф называется r‑валентным или r‑однородным, если любая его вершина имеет степень, равную r.

Например, цикл является 2-валентным графом. На рисунке 32 (а) изображен 3-валентный граф Петерсона, графы Платоновых тел: (б)–куба, (в)‑тетраэдра, (г)–додекаэдра, (д)–4-валентный граф октаэдра и (е)–5-валентный граф икосаэдра.

Л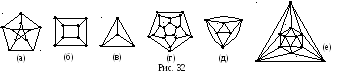 юбой полный граф К_n, где n – число вершин, является (n‑1)‑регулярным.

Граф G=(V, E) называется двудольным, если множество его вершин V можно разбить на два непересекающихся подмножества V₁ и V₂, что каждое ребро графа имеет одну концевую вершину в V₁, а вторую в V₂. См. рис.33 слева. При этом не обязательно, чтобы каждая пара вершин из V₁ и V₂ была соединена ребром. Если же это так, то граф называется полным двудольным графом и обозначается обычно K_m,n, где m и n – число вершин в V₁ и V₂ соответственно. См. рис.33 справа.

В полном двудольном графе число вершин равно m+n, а число ребер mn. Полный двудольный граф вида K_1,n называется звездным.

Граф G=(V, E) называется k‑дольным, если множество его вершин V можно разбить на k попарно непересекающихся подмножеств V₁, V₂,, V_k, что любое ребро имеет одну концевую вершину в V_i, а вторую в V_j, где ij. Полным k‑дольным графом называется такой k‑дольный граф, что любая вершина V_i смежна с любой вершиной из V_j, где ij и i, j=1,2,,k.

Объединение звездного графа K_1,n‑1 и цикла C_n‑1 называется колесом и обозначается W_n.

5. Эйлеровы графы

Знаменитая задача Эйлера о Кёнигсбергских мостах, сформулированная на языке графов в 1736 г., дала начало математической теории графов. Это игровая задача, суть которой заключается в следующем: в городе Кёнигсберге на реке Преголя имеется два острова, которые соединяются между собой и берегами семью мостами, как показано на рис.34. Прогуливаясь по городу и начиная движение из любой точки, требуется пройти по каждому мосту ровно по одному разу и вернуться в исходную точку.

С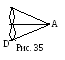опоставим каждому участку суши вершину графа, а каждому мосту – ребро. Тогда «план города» будет выглядеть так, как показано на рис.35. И задачу можно теперь переформулировать для графов: найти в связном графе такую замкнутую цепь, которая проходит через каждое его ребро или, как говорят, покрывает все ребра графа. Такая цепь называется эйлеровой цепью или эйлеровым циклом, а графы, в которых такая цепь существует, называются эйлеровыми графами. Очевидно, что граф, изображенный на рис.35, эйлеровым не является. Граф на рисунке 36 – эйлеров, и соответствующая эйлерова цепь – это последовательность ребер (1,2,,12).

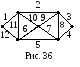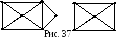Граф называется полуэйлеровым, если в нем существует открытая эйлерова цепь, т.е. цепь, покрывающая все ребра графа, у которой начальная и конечная вершины не совпадают. И, наконец, граф называется неэйлеровым, если в нем не существует ни открытой, ни замкнутой эйлеровой цепи. На рис.37 (слева) – полуэйлеров граф, на рис.37 (справа) – неэйлеров граф.

Теорема: Связный граф является эйлеровым тогда и только тогда, когда любая его вершина имеет четную степень.

Следствие 1: семейство ребер эйлерова графа можно разбить на непересекающиеся по ребрам циклы.

Следствие 2: каждая вершина эйлерова графа содержится хотя бы в одном цикле.

В любом связном графе с 2k нечетными вершинами имеется семейство из k цепей (не пересекающихся по ребрам), которые в совокупности покрывают все ребра графа.

Следствие. Граф является полуэйлеровым тогда и только тогда, когда в нем имеется ровно две вершины нечетной степени. Очевидно, одна из этих вершин будет начальной для открытой эйлеровой цепи графа, а другая – конечной.

Рассмотрим алгоритм Флёри построения эйлеровой цепи в эйлеровом графе.

Пусть G – эйлеров граф, тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины, идем по ребрам графа произвольным образом, соблюдая лишь следующие правила: 1) стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются; 2) на каждом этапе идем по мосту только тогда, когда нет других возможностей.