7 Вопрос: Простейшие методы интегрирования.

1.Непосредственное интегрирование:

Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.

2.Подведение под знак дифференциала:

Данный метод эквивалентен методу замены переменной (см. далее):

3.Метод замены переменной (метод подстановки):

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Пусть требуется вычислить интеграл . Сделаем подстановку где — функция, имеющая непрерывную производную.

Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

4.Интегрирование выражений вида: :

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.

Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.

Если n и m чётные, то удобнее сделать подстановку tg x = t.

Примеры:

Вычислить:

Пусть тогда и

5.Интегрирование по частям:

Интегрирование по частям — применение следующей формулы для интегрирования:

В частности, с помощью n-кратного применения этой формулы находится интеграл где Pn + 1(x) — многочлен (n + 1)-ой степени.

6.Интегрирование рациональных дробей(?!)

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов. Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь , знаменатель которой разложен на множители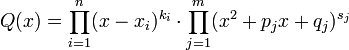

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

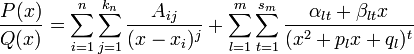
где Aij,αlt,βlt — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

8 Вопрос:Понятие определенного интеграла, св-ва.

Определённый интеграл — аддитивный монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Данное выше определение интеграла в итоге приводит к привычному пониманию определённого интеграла, как площади подграфика функции на отрезке.

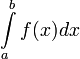
a – нижний предел.

b – верхний предел.

f(x) – подынтегральная функция.

Геометрический смысл-Определённый интеграл как площадь фигуры:

Определённый интеграл 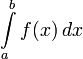численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

Формула Ньютона — Лейбница-главная формула-основная теорема анализа: 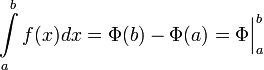, где Ф-первообразная функции , сама функция должна быть непрерывна на отрезке.

Свойства определённого интеграла:

Теорема 1. Определённый интеграл с одинаковыми пределами интегрирования равен нулю, т.е.:

Это свойство содержится в самом определении определённого интеграла. Однако его можно получить и по формуле Ньютона-Лейбница:

Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования, т.е.:

Пусть F(x) – первообразная для f(x). Для f(t) первообразной служит та же функция F(t), в которой лишь иначе обозначена независимая переменная. Следовательно,

.

Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла, т.е.

Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций, т.е.: .

Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям, т.е. если

То :

Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак, т.е:

.

Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его, т.е.:

.

Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если:

Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство :

можно почленно интегрировать, т.е.:

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.