49.Физические основы электрокардиографии

Живые ткани являются источником электрических потенциалов (биопотенциалов).

Регистрация биопотенциалов тканей и органов с диагностической целью получила название электрографии. Такой общий термин употребляется сравнительно редко, более распространены конкретные названия соответствующих диагностических методов: электрокардиография (ЭКГ) – регистрация биопотенциалов, возникающих в сердечной мышце при ее возбуждении, электромиография (ЭМГ) – метод регистрации биоэлектрической активности мышц, электроэнцефалография (ЭЭГ) – метод регистрации биоэлектрической активности головного мозга и др.

В большинстве случаев биопотенциалы снимаются электродами не непосредственно с органа (сердца, головного мозга), а с других, соседних тканей, в которых электрические поля этим органом создаются.

В клиническом отношении это существенно упрощает саму процедуру регистрации, делая ее безопасной и несложной. Физический подход к электрографии заключается в создании (выборе) модели электрического генератора, которая соответствует картине «снимательных» потенциалов.

Все сердце в электрическом отношении представляется как некоторый электрический генератор в виде реального устройства и как совокупность электрических источников в проводнике, имеющем форму человеческого тела. На поверхности проводника при функционировании эквивалентного электрического генератора будет электрическое напряжение, которое в процессе сердечной деятельности возникает на 34б поверхности тела человека. Моделировать электрическую деятельность сердца вполне допустимо, если использовать дипольный эквивалентный электрический генератор. Дипольное представление о сердце лежит в основе теории отведений Эйнтхове-на. Согласно ей сердце есть таковой диполь с диполь-ным моментом, который поворачивается, изменяет свое положение и точку приложения за время сердечного цикла. В. Эйнтховен предложил снимать разности биопотенциалов сердца между вершинами равностороннего треугольника, которые приближенно расположены в правой и левой руке и левой ноге.

По терминологии физиологов, разность биопотенциалов, регистрируемую между двумя точками тела, называют отведением. Различают I отведение (правая рука – левая рука), II отведение (правая рука – левая нога) и III отведение (левая рука – левая нога).

По В. Эйнтховену, сердце расположено в центре треугольника. Так как электрический момент диполя – сердца – изменяется со временем, то в отведениях будут получены временные напряжения, которые и называют электрокардиограммами. Электрокардиограмма не дает представления о пространственной ориентации. Однако для диагностических целей такая информация важна. В связи с этим применяют метод пространственного исследования электрического поля сердца, называемый вектор-кардиографией. Вектор-кардиограмма – геометрическое место точек, соответствующих концу вектора, положение которого изменяется за время сердечного цикла.

50. Уравнение Шредингера. Электрон в потенциальной яме.

 

Основной характеристикой состояния атомов, молекул, элементарных частиц является y-функция. Аналитическое выражение y-функции в каждом конкретном случае можно получить путем решения волнового уравнения – основного урав­нения квантовой механики, предложенного Э. Шредингерам в 1920 г.

Применительно к стационарным состояниям уравнение Шредингера имеет вид:

.       (4.1)

где т – масса частицы; Е и U  – ее полная и потенциальная энергии.

Если частица перемещается только вдоль некоторой линии, например, вдоль оси ОХ (одномерный случай), то уравнение Шрёдингера упрощается и принимает вид:

                  (4.2)

Одним из наиболее простых примеров использования уравнения Шрёдингера является решение задачи о движении частицы в одномерной потенциальной яме.

Пусть электрон перемещается вдоль оси ОХ только в пределах 0<х<l (рис. 4.1). Это означает, что в указанном интервале y-функция отлична от нуля, а вне интервала (х < 0, х³  l) равна нулю.

Так как на частицу в выделенном интервале силовые поля не действуют, то ее потенциальная энергия может иметь любое постоянное значение (наиболее удобно принять U=0). Вне этого интервала электрона нет, поэтому следует считать его потенциальную энергию бесконечно большой. На рис. 4.1 показана графическая зависимость U = f(x). Интервал 0<х<l, удовлетворяющий сформулиро­ванным выше условиям, называют одномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетом  U=0 уравнение Шрёдингера (4.2) для интервала 0<х<l  имеет вид:  

.             (4.3)

Введем обозначение:               ,                           (4.4)

тогда:                                                                             (4.5)

Это уравнение аналогично дифференциальному уравнению гармонического колебания, решение которого:

,               (4.10)

где –амплитуда волновой функции, –ее начальная фаза. Чтобы найти две постоянные  и , а также возможные значения  или Е, рассмотрим граничные условия:

1) при х =0 y = 0. Подставляя эти значения в (4.10), получаем

Физический смысл здесь имеет только одно значение: = 0, откуда .

2) при х =l  y = 0. C учетом  из (4.10) имеем:

Физический смысл здесь имеет только одно значение:

, или , откуда

,                                 (4.7)

где п – целое число, оно принимает значения 1, 2, 3, ...; п ≠ 0, так как в противном случае y= 0 при любом х, что означает отсутствие электрона в потенциальной яме. Число n называют квантовым числом. Из (4.4) находим энергию , что с учетом (4.7) дает:

.                                               (4.8)

Индекс n при Е показывает, что различным значениям квантового числа n соответствует и разная энергия.

Подставляя w (4.7) в (4.5) и учитывая , получаем

.                  (4.9)

Из (4.8) следует, что решение уравнения Шредингера для электрона в потенциальной  яме  без  каких-либо дополнительных  постулатов  приводит к дискретным, квантованным значениям энергии:  ;  и т.д.

Возведя (4.9) в квадрат, получим плотность вероятности  нахождения электрона в разных точках потенциальной ямы. На рис.4.2. показана графическая зависимость от х при разных дискретных состояниях, то есть разных квантовых числах. Как видно из рисунка, электрон может с разной с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в которых вероятность нахождения электрона вообще равна нулю. Это существенно отличается от представлений классической физики, согласно которым равновероятно нахождение частицы в раз­ных местах потенциальной ямы

Теория атома водорода по Бору.

Для объяснения противоречий модели строения атома опытным фактам датский физик Нильс Бор в 1913 г. обобщил гипотезу Планка для любой атомной системы, положив тем самым начало развитию квантовой теории строения атома. В основе теории Бора лежат два постулата:

I. Атомы и атомные системы могут длительное время находиться в определенных состояниях, называемых стационарными, при этом атом не излучает и не поглощает энергию. Энергии стационарных состояний образуют дискретный ряд Е₁, Е₂, Е₃,…

II. Атомы излучают или поглощают энергию при переходе из одного стационарного состояния в другое, при этом квант излучаемой или поглощаемой энергии определяется соотношением: hv=E_n–E_m , где E_n , E_m – энергии стационарных состояний, между которыми произошел переход.

Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем (систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не⁺, Li⁺), а также теоретически вычислить постоянную Ридберга. 

Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами.  Потенциальная энергия взаимодействия электрона с ядром:

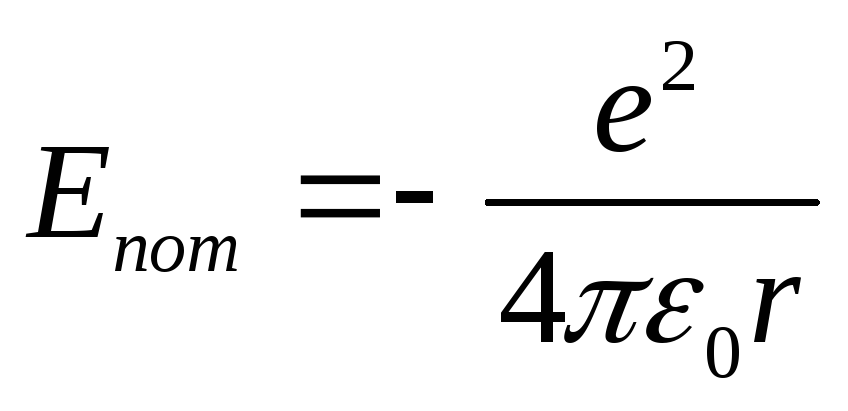                                               (9.1),

r – радиус орбиты. Кинетическая энергия электрона, движущего вокруг ядра:                                                          (9.2).

Тогда полная энергия атома:

              (9.3).

Электрон вокруг ядра движется с ускорением  под действием кулоновской силы:                    .

По второму закону Ньютона (ma = F_k) можно записать:

                                               (9.4);

отсюда                                                                            (9.5).  

Поставим (9.5) в (9.3):                                           (9.6).

По классической механике радиус орбиты электрона может принимать любые значения, тогда и энергия согласно (9.6) может принимать любые значения. Согласно же постулатам Бора энергия атома, а значит и радиус орбиты электрона определенные. Бор предложил правило отбора или правило квантования (третий постулат Бора): из всех возможных орбит электрона осуществляется только те, для которых момент импульса электрона кратен постоянной Планка:

                                     (9.7),

где n=1,2,3,… – главное квантовое число. Используя соотношения (9.4) и (9.7) определим радиус стационарной орбиты электрона:

                   (9.8),

при  (радиус первой орбиты).

Из (9.8) следует . Подставляя (9.8) в (9.10) получим выражение для энергии стационарных состояний:

=                        (9.9)

При  – энергия первого стационарного состояния.

51. Электронные оболочки сложных атомов.

Квантовые числа, описывающие состояние электрона в атоме водорода, используют для приближённой характеристики состояния отдельных электронов сложных атомов. Однако при этом следует учитывать по крайней мере два существенных отличия сложных атомов от атома водорода: 1) в сложных атомах энергия электронов из-за их взаимодействия зависит не только от n, но и от l;

2) распределение электронов по энергетическим уровням обусловлено принципом Паули, согласно которому в атоме не может быть двух (и более) электронов с четырьмя одинаковыми квантовыми числами.

При образовании электронной конфигурации, соответствующей невозбуждённому состоянию атома, каждый электрон стремиться иметь наименьшую энергию. Если бы не принцип Паули, то все электроны расположились бы на самом нижнем энергетическом уровне. В действительности электроны последовательно заполняют состояния, которые указаны для атома водорода в табл. 30 (за некоторыми исключениями).

Электроны с одинаковым квантовым числом образуют слой. Слой обозначают буквами K,L, M, N и т.д в соответствии с n = 1, 2, 3, 4, … . Электроны, имеющие одинаковые пары значений n и l, входят в состав оболочки, которая кратко обозначается так же, как соответствующие состояния для электрона атома водорода: 1s, 2s, 2p и т.д. Так, например, называют 2s-оболочка, 2s-электроны и т.п.

Число электронов в оболочке обозначают справа вверху около символической записи оболочки, например 2p4.

Распределение электронов по оболочкам в атоме (электронные конфигурации) обычно указывают следующим образом: для азота (Z=7) – 1s2, 2s2, 2p3; для кальция (Z=20) – 1s2, 2s2, 2p6, 3s2, 3p6, 4s2 и т.д.

Так как энергия электронов сложных атомов зависит не только от n, но и от l, то построение таблицы Менделеева не всегда происходит постепенным заполнением слоёв по мере усложнения атома. У калия (Z=19), например, вместо заполнения слоя M (что соответствовало конфигурации: 1s2, 2s2, 2p6, 3s2, 3p6, 3d1) начинается заполнение слоя N и создаётся следующая электронная конфигурация: 1s2, 2s2, 2p6, 3s2, 3p6, 4s1. Аналогичные отклонения от «регулярного» заполнения слов имеются и у некоторых других элементов.

Всегда выполняется общее правило: электроны невозбуждённого атома занимают состояние с наименьшей энергией и в соответствии с принципом Паули.

Состояние многоэлектронного атома в целом определяется следующими квантовыми числами: L – квантовым числом полного орбитального момента атома, которое принимает значения 0, 1, 2, 3 и т.д.; J – квантовым числом полного момента атома, которое может принимать значения с интервалом в единицу от |L – S| до L + S; S – квантовым числом результирующего спинового момента атома; минимальным квантовым числом mj, которое определяет дискретные значения проекции полного момента импульса атома LA на некоторую ось Z: LAZ = (h/2П)mj

Энергетический уровень — собственные значения энергии квантовых систем, то есть систем, состоящих из микрочастиц (электронов, протонов и других элементарных частиц) и подчиняющихся законам квантовой механики. Каждый уровень характеризуется определённым состоянием системы, или подмножеством таковых в случае вырождения. Понятие применимо к атомам (электронные уровни), молекулам (различные уровни, соответствующие колебаниям и вращениям), атомным ядрам (внутриядерные энергетические уровни) и т.д.

Электронные энергетические уровни

В современном понятии об орбитальной модели атома, электроны в атоме способны обладать лишь определёнными величинами энергии, и переходить с одного энергетического уровня на другой лишь скачком. Разница между энергетическими уровнями определяет частоту кванта света, выделяемого или поглощаемого при переходе. Каждой паре значений главного квантового числа n и орбитального квантового числа l соответствует определённый уровень энергии, которой может обладать электрон.

Внутриядерные энергетические уровни

Термин появился благодаря исследованию радиоактивности. Радиационное излучение разделяется на три части: альфа-лучи, бета-лучи и гамма-лучи. Исследования показали, что альфа-излучение состоит из ядер гелия-4 (см. альфа-частица), бета-излучение является потоком быстро движущихся электронов, а гамма-лучи являются электромагнитными. Поскольку энергии переходов между различными электронными уровнями недостаточно для возникновения гамма-лучей, стало понятно, что их источник нужно искать внутри атомного ядра, то есть ядро атома само может обладать различными энергетическими уровнями, при переходах между которыми и происходит излучение гамма-квантов. Гамма-лучи расширили спектр известных электромагнитных волн, и все волны короче 10⁻³ нм называются гамма-лучами.