Скорость

СРЕДНЯЯ Характеризует движение тела на определенном участке траектории Вычисляется по формуле (1.3). t - время, за которое тело совершает перемещение S.

МГНОВЕННАЯ Скорость в данный момент времени Вычисляется по формуле (1.3). t - промежуток времени, имеющий малое значение (стремится к нулю).

Из (1.3) следует, что вектор скорости сонаправлен с вектором перемещения. Следовательно, при любом виде траектории вектор мгновенной скорости направлен по касательной в данной точке в сторону движения (рис 7).

Подобно перемещению, вектор скорости можно разложить на составляющие Vx, Vy (рис 8).

Причем:

V = Vx + Vy

Для нахождения проекций используют формулы проекций векторов на ось:

Vx = V cos()

Vy = V sin() (1.5)

tg()= Vy / Vx

В зависимости от угла, между вектором скорости и осью проекция может принимать как положительное так и отрицательное значение.

Повседневные наблюдения показывают, что тела могут менять модуль и направление скорости с течением времени. Поэтому для характеристики быстроты изменения скорости вводят величину - ускорение.

ускорение - физическая величина, равная изменению скорости в единицу времени.

Обозначение: а

Единицы измерения: [ м/с]

Из определения а = (V - Vo) / t (1.6)

Из (1.6) следует, что направление ускорения совпадает с направлением вектора изменения мгновенной скорости (рис 9).

Подобно перемещению и скорости модуль ускорения можно найти через его проекции на оси координат.

а = аx + аy

аx = а cos() (1.7)

аy = а sin()

При прямолинейном движении вектор ускорения коллинеарен векторам скорости и перемещения. При криволинейном движении это совершенно не обязательно. В этом случае полное ускорение тела раскладывают на две составляющие: нормальное и касательное (тангенциальное) ускорение (рис 10).

Так как нормальное и касательное ускорения в общем случае могут менять направление и численное значение с течением времени, то в дальнейшем речь будет идти о их мгновенных значениях.

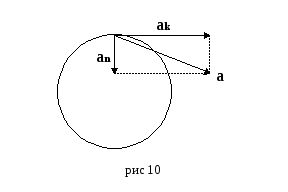
Обозначение: касательное - аk :

Направлено по касательной к траектории в сторону движения тела.

нормальное - аn :

Направлено по нормали к касательной к центру окружности.

По определению нормальное и касательное ускорения перпендикулярны друг другу и :

а = аn + аk (1.8)

Где а - полное ускорение тела.

Наличие нормального ускорения в данной точке показывает, что тело меняет направление движения т.е. направление скорости (но не модуля скорости). В случае движения по окружности с постоянной скоростью модуль скорости не меняется, а меняется лишь ее направление.

Наличие касательного ускорения в данной точке показывает, что тело меняет модуль скорости. При этом нормальное ускорение может равняться нулю. Например в случае прямолинейного движения тела.

Таким образом формула (1.6) приобретает вид:

an + аk = (V - Vo) / t (1.9)

Значение, полученной формулы в том, что она применима к любому виду движений, рассматриваемых дальше. Т.е. появляется возможность описания более частных случаев.

И так, для определения положения тела в любой момент времени вводятся физические величины: перемещение, скорость и ускорение. Это позволяет описать механическое движение тела посредством математических формул. Составление и применение этих формул возможно только в случае выбора системы отсчета.

Далее будут рассмотрены частные случаи движения тел.