#1

Ця форма запису носить назву рівняння (закона) Клапейрона—Менделєєва.

#2

Середня кінетична енергія руху молекули

,

де m — маса частинки, v — її швидкість, k_B — стала Больцмана, T — температура.

Середня швидкість частинок у газі дорівнює

,

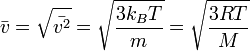де R — газова стала, M — молярна маса.

Абсолю́тна температу́ра (рос. абсолютная температура, англ. absolute temperature, нім. absolute Temperatur f) — параметр стану, який характеризує макроскопічну систему в стані термодинамічної рівноваги..

Абсолютна температура позначається здебільшого великою латинською літерою T й вимірюється в градусах Кельвіна.

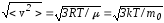– середня квадратична швидкість молекули.

#3

Таким образом, функция распределения молекул по энергиям теплового движения

В механіці можна розглянути також поняття середнього значення абсолютної величини швидкості тіла, що за час t пройшло шлях s. Воно розраховується за простою формулою:

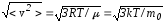– середня квадратична швидкість молекули.

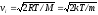– найбільш імовірна швидкість молекул газу

#4 Барометри́чна фо́рмула (рос. барометрическая формула; англ. barometric height formula; нім. barometrische Formel) — формула, за якою визначають залежність тиску або густини газу від висоти. Ця залежність зумовлена дією поля тяжіння Землі і тепловим рухом молекул газу (повітря). Припускаючи, що газ є ідеальним газом сталої температури, і вважаючи поле тяжіння Землі однорідним, отримують барометричну формулу такого вигляду:

,

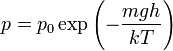Розпо́діл Ма́ксвелла-Бо́льцмана визначає ймовірність того, що частинка ідеального газу перебуває в стані з певною енергією.

Ймовірність того, що частинка перебуває в стані з енергією ε_k згідно з розподілом Больцмана визначається формулою:

,

де μ — хімічний потенціал, T — температура, k_B — стала Больцмана.

Хімічний потенціал μ визначається з умови

∑	nk = 1,
k

Розподіл Больцмана в класичній статистиці

В класичній статистиці частка ідеального газу має лише кінетичну енергію.

Число часток з імпульсами в проміжку  визначається формулою:

,

де m — маса частки.

У випадку коли дана формула виражена через швидкості, а не через імпульси, вона носить назву розподілу Максвелла

.

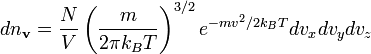#5

Внутрішня енергія ідеального газу описується наступним рівнянням:

#6

Пе́рший зако́н термодина́міки — одне з основних положень термодинаміки, є, по суті, законом збереження енергії у застосуванні до термодинамічних процесів. Перший закон термодинаміки сформульований в середині 19 століття в результаті робіт Саді Карно, Юліуса фон Маєра, Джеймса Прескотта Джоуля і Германа фон Гельмгольца.

Зміна внутрішньої енергії закритої системи, яка відбувається в рівноважному процесі переходу системи із стану 1 в стан 2, дорівнює сумі роботи, зробленої над системою зовнішніми силами, і кількості теплоти, наданої системі: ΔU = A' + Q. Робота здійснена системою над зовнішніми тілами в процесі 1->2 (Назвемо її просто А) A=-A', тоді закон приймає вигляд:

Q = ΔU + A.

Кількість теплоти, що надається системі, витрачається на зміну внутрішньої енергії системи і на здійснення системою роботи проти зовнішніх сил.

Для елементарної кількості теплоти δQ; елементарної роботи δA і малої зміни dU внутрішньої енергії перший закон термодинаміки має вигляд:

δQ = dU + δA

 Для ідеального газу справджується рівняння адіабати

,               (1)

#7

Круговий процес (цикл) в термодинаміці, процес, при якому фізична система (наприклад, пара), зазнавши ряд змін, повертається у вихідний стан. Термодинамічні параметри і характеристичні функції стану системи (температура Т, тиск р,об'єм V, внутрішня енергія U, ентропія S і ін.) в кінці До. п. знов приймають первинне значення і, отже, їх зміни при До. п. дорівнюють нулю (D U = 0 і т. д.). Всі зміни, що виникають в результаті До. п., відбуваються лише в середовищі, що оточує систему. Система (робоче тіло) на одних ділянках До. п. виробляє позитивну роботу за рахунок своєї внутрішньої енергії і кількостей теплоти Q _n , отриманих від зовнішніх джерел, а на ін. ділянках До. п. роботу над системою здійснюють зовнішні сили (частина її йде на відновлення внутрішньої енергії системи). Згідно першому початку термодинаміки (закону збереження енергії), вироблена в До. п. системою або над системою робота ( А ) дорівнює сумі алгебри кількостей теплоти (Q ) , отриманих або відданих на кожній ділянці До. п. (D U = Q — А = 0, А = Q ) . Відношення А / Q _n (досконалою системою роботи до кількості отриманої нею теплоти) називається коефіцієнтом корисної дії (ккд) До. п.

Кругов́ий цикл або замкнений цикл – це сукупність процесів, що повертають систему у першопочатковий стан.

Дру́гий закон термодина́міки — один із основних законів фізики, закон про неспадання ентропії в ізольованій системі.

Формулювання

Для системи із сталою температурою існує певна функція стану S — ентропія, яка визначається таким чином, що

1. Адіабатичний перехід із рівноважного стану A в рівноважний стан B можливий лише тоді, коли

.

2. Приріст ентропії в повільному квазістатичному процесі дорівнює

,

де T — температура.

У найпростішій ідеальній тепловій машині здійснюється так званий цикл Карно, який складається з двох ізотерм і двох адіабат.

Цикл Карно́ — цикл роботи теплового двигуна. Цикл складається з чотирьох стадій:

1. Робоча речовина нагрівається за сталої температури (ізотермічний процес).

2. Робоча речовина розширюється за сталої ентропії (адіабатичний процес).

3. Робоча речовина охолоджується за сталої температури (ізотермічний процес).

4. Робоча речовина стискається за сталої ентропії (адіабатичний процес).

Коефіцієнт корисної дії для двигуна, що працює за циклом Карно, залежить лише від різниці температур нагрівача T_H і охолоджувача T_C.

Для збільшення коефіцієнта корисної дії циклу Карно необхідно зробити температуру нагрівача якомога більшою, а температуру охолоджувача — якомога меншою.

Фо́рмула Карно́, називається на честь Лазаря Карно. Нижче наведено її формулювання. Нехай ABC вписаний в коло трикутник, тоді сума відстаней від центра описаного кола D до сторін трикутника ABC дорівнює:

де r — радіус вписаного кола, а R — радіус описаного кола. Тут знак відстаней береться негативним тоді і тільки тоді, якщо відрізок DX (X = F, G, H) лежить повністю за межами трикутника. На даному рисунку DF — зі знаком мінус, а DG і DH — зі знаком плюс.

#8

Ентроп́ія S — в термодинаміці міра енергії у термодинамічній системі, яка не може бути використана для виконання роботи. Вона також є мірою безладдя, присутнього в системі.

Поняття ентропії

Поняття ентропії було вперше введено у 1865 році Рудольфом Клаузіусом. Він визначив зміну ентропії термодинамічної системи при оборотному процесі як відношення загальної кількості теплоти ΔQ, отриманої або втраченої системою, до величини абсолютної температури T:

Рудольф Клаузіус дав величині S назву «ентропія», утворивши її від грецького слова τρoπή, «зміна» (зміна, перетворення).

Рівність відноситься саме до зміни ентропії. У термодинаміці ентропія визначається лише з точністю до сталої.

Зв'язок між теплоємністю та ентропією дається формулою

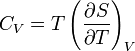
Третій закон термодинаміки

Теорема Нернста, відома також під назвою третій закон термодинаміки, стверджує, що ентропія прямує до нуля при абсолютному нулі температури.

Вперше закон спадання ентропії до нуля при нульовій температурі сформулював Вальтер Нернст (Нобелівська премія з хімії 1920 року).

Обґрунтування

Теорема Нернста базується на квантвомеханічних уявленнях. У класичній фізиці ентропія визначена з точністю до сталої, тому можна стверджувати лише те, що при нульовій температурі ентропія приймає мінімальне значення. Згідно з квантовою механікою при абсолютному нулі температури фізичне тіло перебуває в основному стані. Такий стан єдиний. Оскільки

,

де S — ентропія, k — стала Больцмана, Γ — кількість можливих станів, ентропія системи дорівнює нулю.