
05 семестр / Книги и методические указания / Баловнев Расчет цилиндрических зубчатых передач
.pdf
11
Модули m в мм по стандарту ГОСТ 9563-80
|
|
|
|
|
|
|
|
|
Таблица 5 |
Ряд 1 |
1,5 |
2 |
2,5 |
3 |
4 |
5 |
6 |
8 |
10 |
Ряд 2 |
1.75 |
2,25 |
2,75 |
3,5 |
4,5 |
5,5 |
7 |
9 |
11 |
Задаются ориентировочно углом наклона зубьев β : для косозубых колес редукторов
в пределах 8о...20о , для косозубых колес коробок передач - 20о...30о , для шевронных -
25о...40о .
Определяют числа зубьев z1 и z2
|
|
|
z1 |
= |
2 aw cos β |
, |
|
|
|
(13) |
||
|
|
|
m ( u ± |
1 ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
z2 = z1 u . |
|
|
|
|
|
|
(14) |
|
Полученные значения округляют до целых чисел. |
|
|
|
|
|
|
|
|||||
Примечание. Если число зубьев z1 < 17 , то следует выполнить проверку на |
возможность |
|||||||||||
подрезания зуба по формуле (15). |
|
|
|
|
|
|
|
|
|
|
||
|
zmin = 2 (cos2 β / tg2αw +1) cosβ . |
|
(15) |
|||||||||
Здесь αw = 200 - угол зацепления. |
|
|
|
|
|
|
|
|
|
|
||
2.6.3.2. При |
колесе |
и |
шестерне с |
|
упрочненной поверхностью |
зубьев |
||||||
( H > 45HRC ) |
|
|
|
|
|
|
|
|
|
|
|
|
Из условий равнопрочности по контактным напряжениям и изгибу определяют |
||||||||||||
наибольшее допустимое произведение |
|
|
[σ]F |
|
|
|
|
|||||
|
(z |
Y |
) |
|
= A 103 |
|
u ±1 , |
|
(16) |
|||
|
|
|
|
|||||||||
|
V 1 |
FS |
max |
|
|
[σ]2 |
u |
|
|
|||
|
|
|
|
|
|
|
|
H |
|
|
|
|
где zV 1 - эквивалентное число |
зубьев шестерни; |
YFS - |
коэффициент, |
учитывающий |
||||||||
формулу зубьев и концентрацию напряжений. |
|
|
|
|
|
|
|
|||||
При этом допускаемое напряжение изгиба устанавливают по п. 2.5. Для прямозубых |
||||||||||||
колес A =190 , косозубых и шевронных A = 220 . |
|
|
|
|
|
|||||||
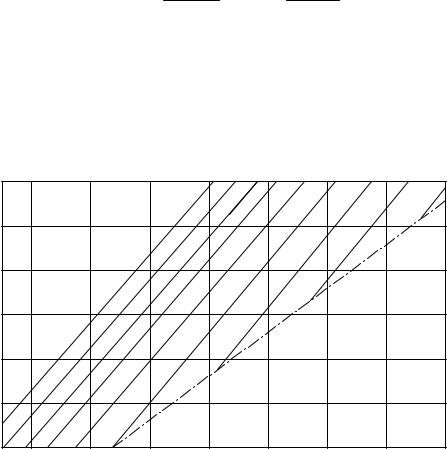
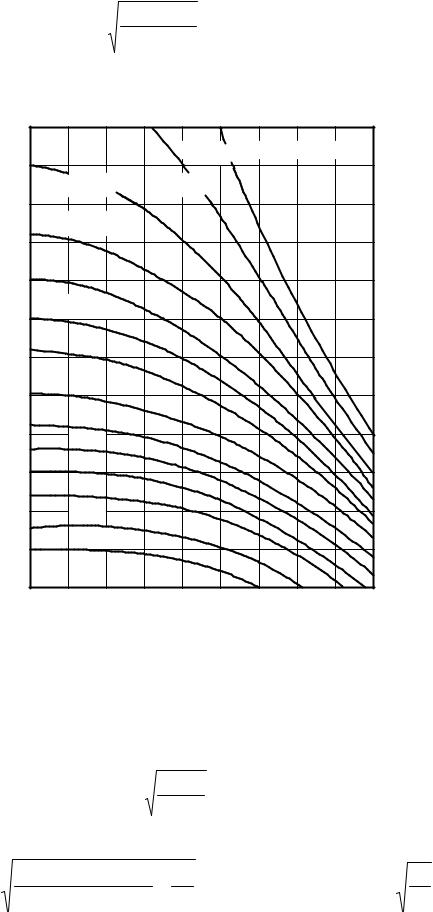
По найденному |
произведению |
( z1 YFS ) |
из |
рис. 4 находят возможные |
zV 1 и |
|||||||
коэффициент смещения x1 . При этом расчет следует вести для нескольких вариантов zV 1 и
x |
1 с тем, чтобы после окончательного определения модуля по п. 2.6.4., угла наклона зуба |
β |
по п. 2.6.5. и коэффициента осевого перекрытия εβ по п. 2.6.6. выбрать более |
целесообразный вариант.
12
Примечания:
1. Если определенное по формуле (16) произведение ( z1 YFS ) при данном zV 1
оказывается больше величин, соответствующих на рис. 4 линии а −а, то лимитирующим является контактное напряжение и смещение определяется только условием отсутствия подрезания.
2. Следует иметь в виду, что рис. 4 дает значение коэффициента смещения x1 при данном zV 1 из условия равнопрочности по контактным напряжениям и изгибу при диаметре dw1 , определенному по контактным напряжениям. Поэтому с увеличением числа зубьев zV 1 модуль уменьшается и требует большее смещение x1 .
Задаются ориентировочно углом наклона зубьев β согласно п. 2.7.3.1. и определяют числа зубьев:
z |
= z |
cos3 β |
и |
z |
2 |
= z |
1 |
u . |
|
|
Округляют |
|
z |
1 |
|
и |
z |
2 |
до |
целых |
чисел. |
Находят |
||||||||||||||
1 |
V 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
эквивалентные числа зубьев |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
z |
|
= |
|
|
z1 |
|
|
|
|
|
и |
z |
= |
|
|
z2 |
β |
, |
|
|
|
|
(17) |
|||||||
|
|
|
|
|
|
V |
1 |
|
cos3 β |
|
|
|
|
|
V2 |
|
|
cos3 |
|
|
|
|
|
|
||||||||||||
и по блокирующему контуру в приложении 3 к ГОСТ 16532-70 проверяют допустимость |
||||||||||||||||||||||||||||||||||||
смешение |
x1 и находят смещение |
x2 . При z1 + z2 < 60 рекомендуется равносмещенная |
||||||||||||||||||||||||||||||||||
передача, т.е. x2 = −x1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Графики для определения ( z1 YFS ) |
|
|
|
|
||||||||||||||||||||||||||
|
zV1 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
= |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
17 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
6 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70 (zV1 YF S ) |
|
||||
|
|
40 |
|
45 |
|
|
50 |
|
|
|
|
|
55 |
|
|
|
|
|
60 |
|
|
|
65 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
13
2.6.4. Определяют модуль
m = |
2 dw1 |
cos β |
|
|
|
(18) |
|
z1 |
|
||
|
+ z2 |
||
иокругляют его до стандартного по табл. 5 п. 2.7.3.1.
2.6.5.Находят окончательно:
передаточное число |
u = |
z2 |
; |
|
|
|
|
|
|
|
(19) |
|
|
|
|
|
|
|
|
|
|||||
|
|
z |
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
||
угол наклона зуба β ( cos β ); |
|
|
|
|
|
|
|
|||||
β = arccos |
m ( z1 + z2 ) |
; |
(20) |
(cosβ = |
m ( z1 + z2 ) |
); |
(20а) |
|||||
|
|
|||||||||||
|
|
|
|
2 aw |
|
|
|
|
2 aw |
|
||
( β фиксируется до минут или четвертого знака после запятой; |
cos β - до шестого знака |
|||||||||||
после запятой); |
|
|
|
|
|
|
|
|
|
|
|
|
осевой шаг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
px = |
π m |
. |
|
|
(21) |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
sin β |
|
|
|
|
|
2.6.6. Определяют коэффициент осевого перекрытия |
|
|
|
|||||||||
|
|
|
|
εβ |
= bw2 / px , |
|
|
(22) |
||||
который рекомендуется εβ ≥1,1. В крайнем случае не менее 0,9 . |
|
|||||||||||
Расчет геометрии по п.п. 2.6.3. - 2.6.6. целесообразно вести в нескольких вариантах.
Выбирают тот, у которого u ближе к заданному, а εβ ≥ 1. |
|
||||||||
2.6.7. Диаметры зубчатых колес |
|
|
|
|
|
|
|||
2.6.7.1. Делительные диаметры |
|
|
|
|
|
|
|||
d |
= |
m z1 |
; |
d |
2 |
= |
m z2 |
. |
(23) |
|
|||||||||
|
|
||||||||
1 |
|
cosβ |
|
|
cosβ |
|
|||
2.6.7.2. Диаметры вершин зубьев: |
|
|
|
|
|
|
|||
колес внешнего зацепления |
|
|
|
|
|
|
|
|
|
da1 =d1 +2 m (1 + x1 − y ); |
da2 =d2 +2 m (1+x1 −y); |
(24) |
|||||||
колес внутреннего зацепления |
|
|
|
|
|
|
|
|
|
da1 =d1 +2 m (1 + x1 ); |
da2 =d2 −2 m (1−x1 −0,2); |
(24а) |
|||||||
где x1 и x2 - коэффициенты смещения |
шестерни и колеса; y = −( aw −a ) / m - |
||||||||
коэффициент воспринимаемого смещения; a = 0,5 m ( z2 ± z1 ) - делительное межосевое
14
расстояние. |
|
|
|
|
|
|
|
|
2.6.7.3. Диаметры впадин: |
|
|
|
|
|
|
|
|
колес внешнего зацепления |
|
|
|
|
|
|
|
|
df1 =d1 −2 m (1,25−x1 ); |
df 2 =d2 −2 m (1,25−x2 ); |
(25) |
||||||
колес внутреннего зацепления |
|
|
|
|
|
|
|
|
df1 =d1 −2 m (1,25−x1 ); |
df 2 =d2 +2 m (1,25−x2 ). |
(25а) |
||||||
2.6.7.4. Начальные диаметры |
|
|
|
|
|
|
|
|
dw1 |
= |
2 aw |
|
dw2 = |
2 |
aw u |
|
(26) |
u ±1 |
|
u ±1 |
||||||
|
|
|
|
|
||||
Примечание. Диаметры и контрольные размеры колес находят с точностью до сотых долей мм выполняют проверку по формуле d1 + d2 = 2 aW .
2.6.7.5. Уточнение коэффициента относительной ширины зубчатого венца ведут по формуле
ψbd = |
bw2 |
. |
(27) |
|
|||
|
dw1 |
|
|
Если его величина выходит за рекомендуемые пределы по табл. 3, то степень точности колес корректируют.
2.6.8. Коэффициент торцового перекрытия передачи без смещения находят по формуле
|
|
|
|
εα = εα1 +εα2 , |
|
|
(28) |
||||||
где εα1 |
и εα2 - составляющие коэффициента торцового перекрытия шестерни и |
||||||||||||
колеса соответственно по рис. 5. |
|
|
|
|
|
|
|
|
|
||||
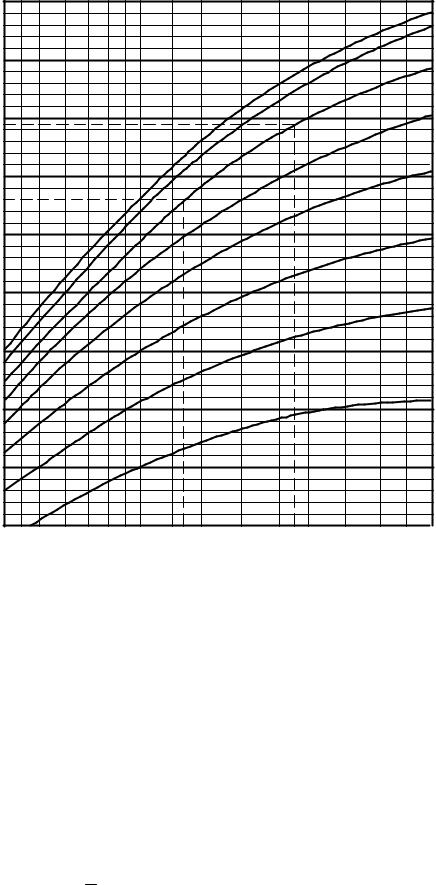
Пример. Дано: |
z = 27 , |
z |
2 |
= 55 , |
β = 150 . |
По |
графику определяем |
(см. пунктир) |
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
εα1 = 0,78 , а εα2 = 0,845 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
При β |
< 20o коэффициент торцового перекрытия можно определять по формуле |
||||||||||||
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
1 |
|
|
cos β . |
|
|||
|
εα |
|
|
|
|
± z |
|
(28а) |
|||||
|
= 1,88 − 3,2 z |
2 |
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|||
Примечание. Для передач со смещением коэффициент торцового перекрытия передачи находят по приложению 2 ГОСТ21354-87.
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
График для определения εα1 и εα2 |
|
|
||||||
ea |
|
|
|
|
|
|
|
|
|
|
|
b=0o |
|
|
|
|
|
|
|
|
|
|
|
|
8o |
0,9 |
|
|
|
|
|
|
|
|
|
|
|
15o |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,85 |
|
|
|
|
|
|
|
|
|
|
|
20o |
0,8 |
|
|
|
|
|
|
|
|
|
|
|
25o |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
|
|
|
|
|
|
|
30o |
0,7 |
|
|
|
|
|
|
|
|
|
|
|
35o |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,65 |
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
40o |
0,55 |
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
8 |
9 10 |
12 |
14 16 18 20 |
25 |
30 |
40 |
50 |
60 |
80 |
100 120 |
z |
|
|
|
|
|
|
Рис. 5 |
|
|
|
|
|
|
2.6.9. Суммарный коэффициент перекрытия находят по формуле |
|
|||||||||||
εγ = εα +εβ . |
(29) |
2.7.Размеры для контроля взаимного положения разноименных профилей
2.7.1.Постоянная хорда, выраженная в долях модуля
sc* = π |
cos2 α + x sinα . |
(30) |
2 |
|
|
2.7.2. Постоянная хорда |
|
|
|
sc = sc* m |
(31) |
2.7.3. Высота до постоянной хорды |
|
|
hc = 0,5 [(da −d )− m sc* tgα] |
(32) |
|
16
2.8.Скорость и силы в зацеплении
2.8.1.Окружная скорость
V = π dw1 n1 .
60000
2.8.2. Окружная сила
F = 2000 T2 .
t dw2
2.8.3. Радиальная сила
Fr = Ft costgαβw .
2.8.4. Осевая сила
Fx = Ft tgβ .
2.9. Проверка заготовок колес на прокаливаемость
(33)
(34)
(35)
(36)
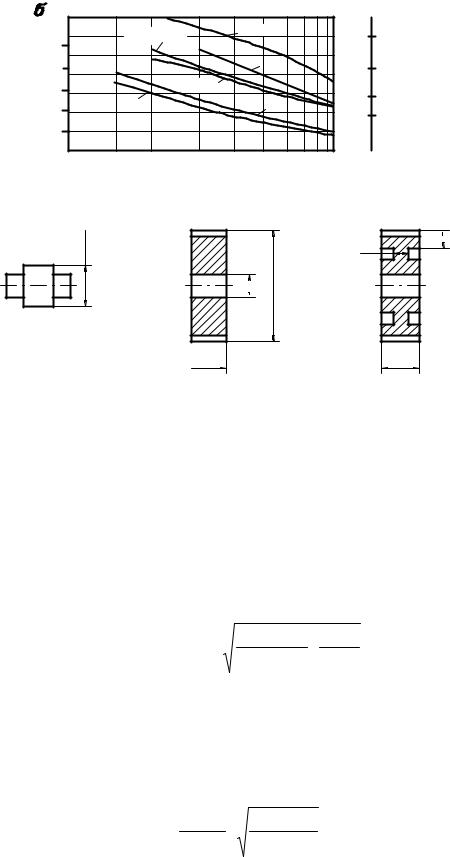
Окончательный выбор марки стали при колесах с упрочненной поверхностью должен проводиться с учётом прокаливаемости в зависимости от предела прочности σв или твердости HB ( HRC ) сердцевины по рис. 6, для улучшенных колес - по рис.7.
Размеры, определяющие прокаливаемость, устанавливаются по рис.8.
σв , |
HB и HRC сердцевины сталей с поверхностным упрочнением |
|||||
|
в |
|
25Х ГТ |
H B H RCЭ |
||
|
МПа |
|
||||
|
|
|
|
|||
|
1500 |
|
|
|
400 |
|
|
1400 20ХН 2М |
|
|
|
||
|
|
30Х ГТ |
360 40 |
|||
|
1300 |
|
|
|
|
|
|
1200 |
|
|
25ХГМ |
320 |
35 |
|
1100 |
|
|
|
|
|
|
|
|
|
280 |
30 |
|
|
1000 12ХН3А |
|
20ХН 3А |
|||
|
|
240 25 |
||||
|
900 |
|
|
18ХГТ |
||
|
800 |
|
|
|
200 |
20 |
|
700 |
|
|
20Х Н |
|
|
|
|
|
|
|
||
|
600 |
|
|
|
|
|
|
10 |
15 |
20 |
30 40 50 60 80 S мм |
|
|
|
|
|
|
Рис.6 |
|
|
|
|
|
17 |
|
|
|
σв , |
HB и HRC улучшенных сталей |
|
||
в |
|
|
40ХН |
H B H RCЭ |
|
МПа |
|
40ХН2М А |
325 35 |
||
|
|
||||
1100 |
|
|
|
300 |
|
1000 |
|
|
40Х |
30 |
|
|
|
275 |
|||
|
40ХФА |
||||
900 |
|
250 |
25 |
||
|
40 |
45 |
|||
800 |
|
225 |
20 |
||
|
|
|
|||
700 |
|
|
|
200 |
|
10 |
15 |
20 |
30 40 50 60 80 S мм |
|
|
|
|
|
Рис. 7 |
|
|
|
Размеры, определяющие прокаливаемость |
|
|||
da
d da
da
 b
b
K
S
b
S = |
da |
+3мм |
меньшее из двух |
большее из двух |
||
|
||||||
2 |
|
|
da −d |
|
|
|
|
|
|
S = |
или S = b |
S = ( 5...6 ) m или S = K , |
|
|
|
|
|
|||
|
|
|
2 |
|
K = ( 0,4...0,5 ) b |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8 |
|
|
3.ПРОВЕРОЧНЫЙ РАСЧЕТ ПО КОНТАКТНЫМ НАПРЯЖЕНИЯМ
3.1.Расчет на сопротивление усталости для стальных колес производят по формуле
σ |
H |
= 190 Z |
H |
Z |
ε |
Ft K H |
u ± 1 ≤ [σ ] . |
( 37) |
|
|
|
|
bw 2 dw1 u |
H |
|
||||
|
|
|
|
|
|
|
|
||
Передаточное число u, ширину колеса bw2 и |
начальный диаметр шестерни dw1 |
||||||||
берут из геометрических расчетов п. 2.6.3...2.6.7.
3.1.1. Коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления
при x ≠ 0 и x |
2 |
≠ 0 - |
Z |
H |
= 1 |
2 cos βв ; |
(38) |
1 |
|
|
cosαt |
tgαtw |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
при x |
= x |
2 |
= 0 - |
Z |
H |
= |
4 cos βв |
; |
|
|
|
(38а) |
||
1 |
|
|
|
|
|
sin 2 αt w |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или по рис. 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент ZH |
|
|
|
|||
|
|
ZH |
|
|
|
|
|
-0,02=(x1+x2)/(z1+z2) |
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
2,7 |
-0,015 |
|
-0,015 |
|
|
|
|
|||||
|
|
-0,005 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2,5 |
0,0 |
|
|
|
|
|
|
|
||||
|
|
0,005 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2,3 |
0,01 |
|
|
|
|
|
|
|
||||
|
|
0,02 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2,1 |
0,03 |
|
|
|
|
|
|
|
||||
|
|
0,04 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0,05 |
|
|
|
|
|
|
|
||
|
|
1,9 |
0,06 |
|
|
|
|
|
|
|
||||
|
|
0,08 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
1,7 |
5 |
|
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
||
|
|
|
|
0 |
|
b |
||||||||
|
|
|
|
|
|
|
|
|
Рис. 9 |
|
|
|
|
|
Здесь αt |
- |
делительный угол профиля в торцовом сечении; αtw - угол зацепления; |
||||||||||||
βв - основной угол наклона.
3.1.2.Коэффициент, учитывающий суммарную длину контактных линий
Для прямозубых колес |
Zε = |
4 −εα . |
|
|
|
(39) |
|||
|
|
|
|
3 |
|
|
|
|
|
Для косозубых и шевронных колес: |
|
|
|
|
|
|
|
||
при εβ <1 - Zε = |
( 4 −εα ) |
(1 −εβ ) |
+ |
εβ |
; (40) при εβ |
≥1 - |
Zε = |
1 |
(40а). |
3 |
|
εα |
εα |
||||||
|
|
|
|
|
|
|
|||
Примечание. Для прямозубых колес без смещения при α = 20о ZH Zε = 2,25 .
19
3.1.3 Коэффициент нагрузки
|
|
|
KH = K A KHV KHβ KHα ; |
|
|
|
(41) |
|||||
3.1.3.1. Коэффициент, учитывающий внешнюю динамическую нагрузку K A |
||||||||||||
Если |
циклограмма нагружения |
включает внешние |
динамические |
нагрузки, то |
||||||||
K A = 1 . В противном случае при расчётах на сопротивление усталости |
K A |
принимают |
||||||||||
по табл. 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициент внешней динамической нагрузкиK A |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Таблица 6 |
|
|
Тип двигателя |
|
|
|
Тип рабочей машины |
|||||||
|
|
|
|
|
|
I |
|
II |
|
III |
|
IV |
Электродвигатель; |
паровые |
и газовые |
1,00 |
|
1,25 |
|
1,5 |
|
1,75 |
|||
турбины |
при |
|
стабильных |
режимах |
|
|
|
|
|
|
|
|
эксплуатации |
и |
небольших |
пусковых |
|
|
|
|
|
|
|
||
моментах. |
|
|
|
|
|
|
|
|
|
|
|
|
Гидравлические |
двигатели, |
паровые |
и |
1,10 |
|
1,35 |
|
1,60 |
|
1,85 |
||
газовые турбины при больших часто |
|
|
|
|
|
|
|
|||||
возникающих пусковых моментах. |
|
|
|
|
|
|
|
|
||||
Многоцилиндровый |
двигатель |
внутреннего |
1,25 |
|
1,50 |
|
1,75 |
|
2,00 и |
|||
сгорания. |
|
|
|
|
|
|
|
|
|
|
|
выше |
Одноцилиндровый |
двигатель |
внутреннего |
1,50 |
|
1,75 |
|
2,00 |
|
2,25 и |
|||
сгорания. |
|
|
|
|
|
|
|
|
|
|
|
выше |
Тип рабочей машины:
I – электрический генератор; равномерно работающие ленточные, пластинчатые конвейеры; легкие подъемники; вентиляторы; мешалки для веществ равномерной плотности; турбокомпрессоры; легкие центрифуги; механизмы с вращающимися деталями.
II - неравномерно работающие ленточные, пластинчатые конвейеры; шестеренчатые и ротационные насосы; приводы станков; тяжелые подъемники; центрифуги; механизмы кранов; ; мешалки для веществ с переменной плотностью; поршневые многоцилиндровые насосы; экструдеры; каландры; вращающиеся печи; станы холодной прокатки.
III – экструдеры и мешалки для резины и пластмасс; легкие шаровые мельницы; деревообрабатывающие станки; одноцилиндровые поршневые насосы; нереверсивные станы горячей прокатки; подъемные машины.
IV – экскаваторы; черпалки; тяжелые шаровые мельницы; резиносмесители; дробилки; кузнечные машины; тяжелые насосы; буровые машины; прессы; реверсивные станы горячей прокатки.
3.1.3.2. Коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении назначают по табл. 7.
20
Коэффициент KHV
|
|
|
|
|
|
|
|
|
|
Таблица 7 |
||
Степень |
|
Твердость зубьев |
|
Коэффициент KHV при скорости V в м/с |
|
|||||||
точности |
|
колеса |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
4 |
6 |
|
8 |
|
10 |
|||
|
|
|
|
|
|
|
||||||
6 |
|
Н2 ≤ 350НВ |
_ |
|
_ |
|
_ |
1,18 |
|
1,25 |
|
1,32 |
|
|
|
|
|
|
|
1,06 |
|
1,09 |
|
1,13 |
|
|
|
H2 ≥ 45HRC |
_ |
|
_ |
|
_ |
1,12 |
|
1,16 |
|
1,20 |
|
|
|
|
|
|
|
|
1,04 |
|
1,06 |
|
1,08 |
|
|
Н2 ≤ 350НВ |
_ |
|
_ |
|
1,16 |
1,24 |
|
1,32 |
|
1,40 |
7 |
|
|
|
|
|
|
1,07 |
1,10 |
|
1,13 |
|
1,16 |
|
H2 ≥ 45HRC |
_ |
|
_ |
|
1,09 |
1,14 |
|
1,19 |
|
1,25 |
|
|
|
|
|
|
|
|
1,04 |
1,06 |
|
1,08 |
|
1,10 |
|
|
Н2 ≤ 350НВ |
1,05 |
|
1,10 |
|
1,20 |
1,28 |
|
1,38 |
|
1,48 |
8 |
|
|
1,02 |
|
1,04 |
|
1,08 |
1,12 |
|
1,15 |
|
1,19 |
|
H2 ≥ 45HRC |
1,03 |
|
1,06 |
|
1,12 |
1,18 |
|
1,24 |
|
1,30 |
|
|
|
|
1,01 |
|
1,02 |
|
1,05 |
1,07 |
|
1,09 |
|
1,12 |
|
|
Н2 ≤ 350НВ |
1,06 |
|
1,11 |
|
1,22 |
_ |
|
_ |
|
_ |
9 |
|
|
1,02 |
|
1,04 |
|
1,08 |
|
|
|
|
|
|
H2 ≥ 45HRC |
1,03 |
|
1,06 |
|
1,13 |
_ |
|
_ |
|
_ |
|
|
|
|
1,01 |
|
1,02 |
|
1,05 |
|
|
|
|
|
Примечание. |
В числителе приведены |
значения |
для прямозубых, в |
знаменателе |
– для |
|||||||
косозубых и шевронных колес.
3.1.3.3. Коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий KHβ , уточняют по рис.1 и откорректированному по результатам
проектного расчета коэффициенту относительной ширины зубчатого венца ψbd .
Примечание. При уточненном расчёте зубчатой пары KHβ находят по ГОСТ 21354-87 с
учётом упругой линии вала, зазоров в подшипниках и жесткостей зубьев.
3.1.3.4. Коэффициент, учитывающий неравномерность распределения нагрузки по парам зубьев
K Hα =1 +( K H0 α −1 ) K Hw . |
(42) |
Здесь K Hw - коэффициент, учитывающий приработку зубьев, находят по рис. 10.
В приближенных расчетах для точных зубчатых колес, начиная с 5-й степени
точности, при твердости колеса и шестерни более 350HB принимают |
K H0 α =1 . Для |
|||
степеней точности nCT = 6...9 по формуле |
|
|
|
|
K 0 |
=1 + 0,25 ( n |
−5 ) (1 / Z 2 |
−1 ) . |
(43) |
Hα |
CT |
ε |
|
|
При твердости шестерни или колеса меньше или равной 350HB по формуле
