Задачи к практическому занятию № 1

Для совместной работы на доске

Задача 1.1

Определить размерность производной физической величины объема V, рассчитываемой по формуле V=a·b·h , где a,·b,·h – габаритные размеры длина, ширина и высота соответственно.

Dim V=L·L·L=L³

Задача 1.2

Определить размерность производной физической величины скорости υ, равной первой производной от перемещения по времени.

υ =dl / dt

Dim υ =L / T=LT ^–1

Задача 1.3

Определить размерность производной физической величины угловой скорости ω, равной первой производной от угла поворота по времени.

ω =dφ / dt

Dim ω =1/ T=T ^–1

Задача 1.4

Определить размерность производной физической величины силы F, являющейся мерой механического воздействия на тело со стороны других тел и рассчитываемой по II Закону Ньютона F=ma , где m – масса тела, а – его ускорение, равное второй производной от перемещения по времени.

F =m·dl / d²t

Dim F=M·L /T ²=M·L·T ^–2

Для самостоятельной работы

Задача 1.5

Определить размерность производной физической величины ускорения а, равного первой производной от скорости по времени.

Ответ: Dim а = LT ^–1

Задача 1.6

Определить размерность производной физической величины углового ускорения ε, равного первой производной от угловой скорости по времени.

Ответ: Dim ε =T ^–2

Задача 1.7

Определить размерность производной физической величины плотности тела ρ, равной отношению массы элемента тела dm к объему этого элемента dV.

Ответ: Dim ρ = ML ^–3

Задача 1.8

Определить размерность производной физической величины давления Р, равного отношению силы dF, действующей на элемент поверхности нормально (перпендикулярно) к ней, к площади dS этого элемента.

Ответ: Dim Р = M·L^–1·T ^–2

Задача 1.9

Определить размерность производной физической величины электрического заряда Q, равного произведению силы тока I на время t, в течение которого шел ток.

Ответ: Dim Q = IT

Лекция №3. Основы технических измерений

Ввести понятие измерительной задачи и составляющие ее элементы. Ввести следующие понятия: истинное значение, действительное значение, погрешность. Рассказать об источниках появления погрешностей и привести классификацию погрешностей.

Ввести понятие метрологической характеристики и дать определение основным метрологическим характеристикам.

Рассказать о регулировке и градуировке средств измерений, их целях и способах.

Привести классификацию измерений по числу измерений и рассмотреть алгоритмы обработки результатов однократных и многократных измерений.

Практическое занятие №2. Алгоритмы обработки многократных измерений

Мероприятие	Время проведения	Примечание
Теоретическая база	20 минут
Совместное решение на доске типовых задач	20 минут
Выдача задач для самостоятельного решения	5 минут
Самостоятельное решение задач обучающимися	45 минут	Задачи решаются самостоятельно в аудитории и в конце занятия показываются преподавателю для начисления баллов за практическое занятие. За каждую решенную самостоятельно задачу начисляется 1 балл, но максимально 4 балла за занятие.

Диапазон измерительных величин и их количество постоянно растут, и поэтому возрастает и сложность измерений. Они перестают быть однократным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.

В случае, когда случайная составляющая погрешности однократного измерения может превысить требуемые по условиям задачи значение, выполняют ряд последовательных отдельных измерений и получают одно многократное измерение, погрешность которого может быть уменьшена методами математической статистики.

Из опыта известно, что ни одно измерение, как бы тщательно оно не проводилось, не может дать абсолютно точный результат, вследствие чего часто говорят о наличии ошибок и погрешностей при проведении измерительного эксперимента. Всегда существует множество факторов, в том числе и случайных, приводящих к искажениям получаемой измерительной информации.

При условии исключения из результатов экспериментов систематических и грубых ошибок, остается лишь случайная составляющая погрешности. Случайную ошибку можно рассматривать как суммарный эффект действия многих факторов, каждый из которых не проявляет себя отчетливо. Поэтому случайные ошибки при многократных измерениях получаются различными как по величине, так и по знаку. Их невозможно учесть как систематические, но можно учесть их влияние на оценку истинного значения измеряемой величины. Анализ случайных ошибок является важнейшим разделом математической обработки экспериментальных данных.

В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале.

При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.

Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами.

Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения.

Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.

Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин – моментов.

Начальным моментом n–го порядка результатов наблюдений называется интеграл вида

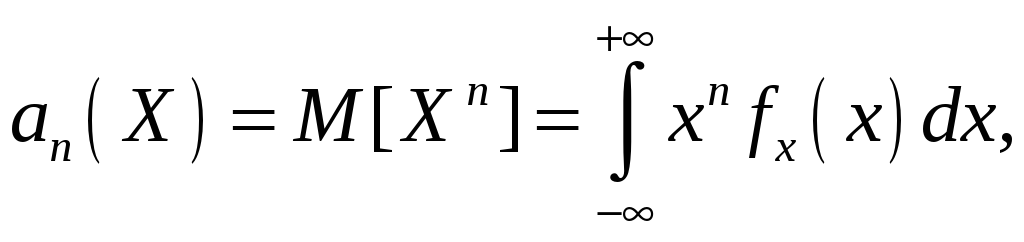
представляющий собой математическое ожидание степени Хⁿ.

При n=1

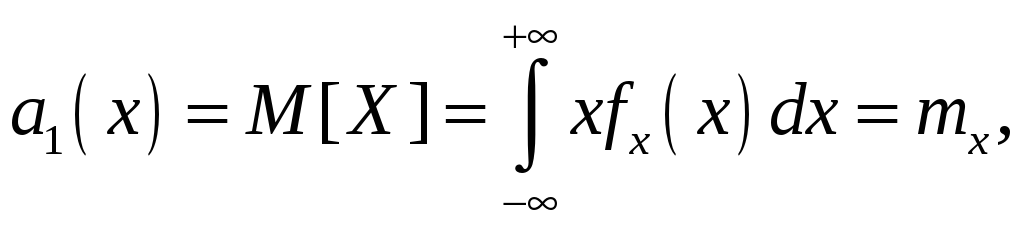
т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений.

Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины математическое ожидание результатов наблюдений.

Центральным моментом n–го порядка результатов наблюдений называется интеграл вида

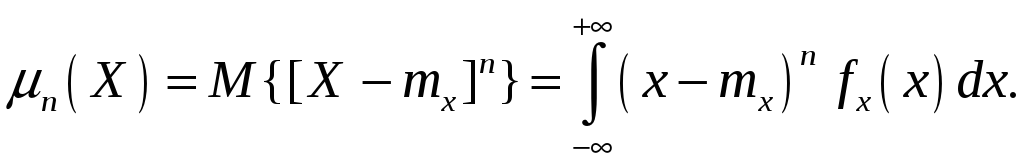
Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений.

При n=2

Дисперсия D[X] случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания.

Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений:

С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины ε, т.е. вероятность P{|δ|}< ε. Для этого рассмотрим формулу, известную как неравенство Чебышева:

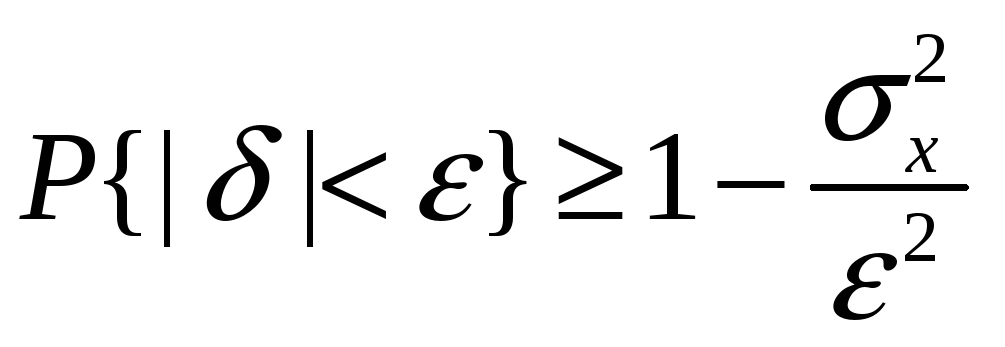или .

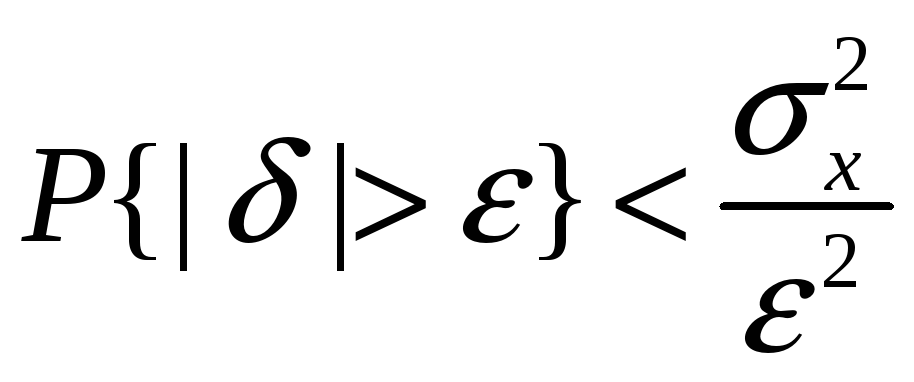Полагая ε = 3σ_х, можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т. е. вероятность того, что случайная погрешность окажется больше 3σ_х:

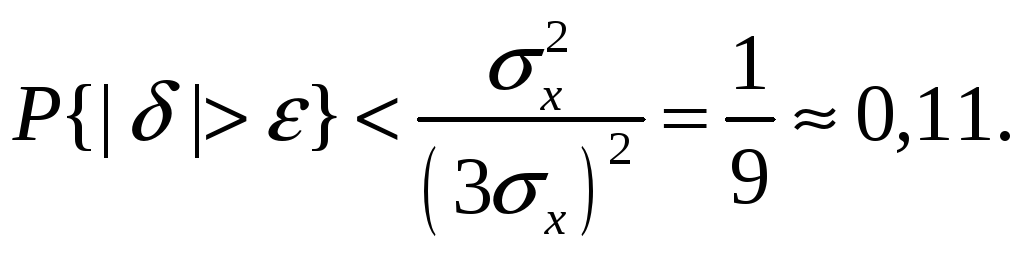
Вероятность того, что погрешность измерения не превысит 3σ_х, составит соответственно P{|δ|}< ε ≥1 – 0,11=0,89.

Неравенство Чебышева дает только нижнюю границу для вероятности P{|δ|}< ε, меньше которой она не может быть ни при каком распределении. Обычно P{|δ|}< ε значительно больше 0,89. Так, например, в случае нормального распределения погрешностей эта вероятность составляет 0,9973.

Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют наиболее важные черты распределения: положение центра распределения и степень его разбросанности. Для более подробного описания распределения используются моменты более высоких порядков.

При практической обработке результатов измерений необходимо последовательно выполнить следующие операции

1. Записать результаты измерений;

2. Вычислить среднее значение из n измерений:

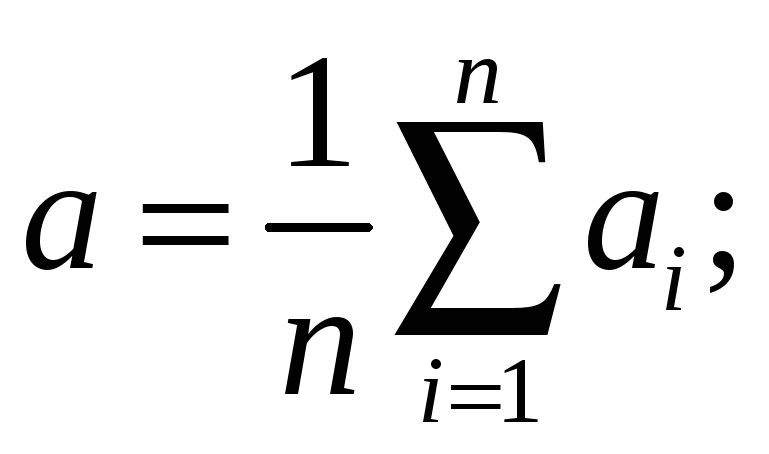
3. Определить погрешности отдельных измерений V_i  а  а_i;

4. Вычислить квадраты погрешностей отдельных измерений V_i²;

5. Если несколько измерений резко отличаются по своим значениям от остальных измерений, то следует проверить не являются ли они промахом. При исключении одного или нескольких измерений п.п.1...4 повторить;

6. Определить среднюю квадратичную погрешность результата серии измерений: