1.1.Уравнение состояния газов.
Аналитическая
зависимость между параметрами состояния
системы называется уравнением состояния.
Для простого тела уравнение состояния:
Этому уравнению простого тела можно придать следующий вид:
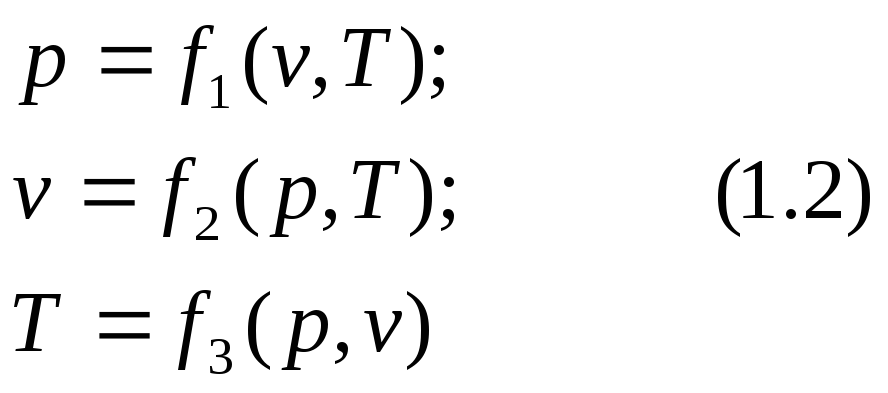
Данные уравнения называют уравнениями состояния простого тела. В термодинамике рассматриваются процессы: изохорный, изотермический, изобарный, адиабатный, политропный. Политропный процесс является обобщающим. Диаграммы круговых процессов (циклов) часто используются в термодинамике для наглядного представления положительной работы двигателей. Идеальный газ можно представить как систему материальных частиц, не обладающих объёмом и силами молекулярного взаимодействия.
В реальных газах имеет место межмолекулярное взаимодействие, а также нельзя пренебрегать собственным объёмом молекул. Реальные газы близки к идеальным, если они находятся в состоянии разрежения или давлении не превышающим атмосферное.
Уравнение состояния идеального газа было получено Клапейроном в 1834 г. и имеет вид:
Для 1 киломоля газа уравнение получено Менделеевым Д.И.:
Объём 1 киломоля
любого газа равен 22,4146 нм
,
р=101325 Па, T=273,15К,
Соответственно универсальная газовая постоянная –
Уравнение состояния, приближённо отражающее свойства реальных газов:
носит название уравнения Ван-дер-Ваальса, где «а» и «b» const.
1.2. I. Законы термодинамики.
Первый закон
термодинамики – частный случай всеобщего
закона природы, т.е. закона сохранения
и превращения энергии применительно к
тепловым процессам. Если газу сообщить
количество теплоты dQ,
то часть её идёт на изменение энергии
газа dU
(внутренняя энергия), а другая часть на
совершение работы dL
против сил внешнего давления «р».
Перемещение поршня dx,
элементарная работа:
интегрируя данное
выражение в пределах от V
до V
,
находим работу:
Обычно в термодинамике
используют удельные значения
соответствующих величин, т.е.
здесь
v-
удельный объём рабочего тела.
Данные соотношения
справедливы для равновесных процессов,
однако с известной долей приближения
их используют для практических
термодинамических расчётов. Для простого
тела внутренняя энергия функция двух
параметров: u=f
(р,T);
u=f
(р,v);
u=f
(v,T)
(1.9).
Таким образом, первый закон термодинамики можно сформулировать в такой редакции – теплота, которой обменивается термодинамическая система с окружающей средой, равна изменению внутренней энергии этой системы и работе, совершаемой в процессе изменения состояния термодинамической системы, т.е. dq=du+рdv (1.10)
Полная теплоёмкость системы равна:
На практике
пользуемся понятием удельной теплоёмкости.
Различают удельную массовую, объёмную,
мольную теплоёмкости. Изохорная
теплоёмкость с
определяет скорость изменения внутренней
энергии системы при T=var
в процессе v=const.
Для изобарного процесса теплоёмкость
с
найдём воспользовавшись выражением:
разделив это
выражение на dT
Получим:
т.к. «u»
не зависит от объёма «v»,
поскольку отсутствуют
силы межмолекулярного взаимодействия,
т.е.
кроме того
,
соответственно
,
это уравнение Майера. Для реальных газов
.
Среднее значение теплоёмкости в
определённом интервале температур
определяется из выражения:
В термодинамических расчётах часто используется вспомогательная функция – энтальпия «H» . Данная функция равна сумме «U» и произведения давления на объём термодинамической системы, Дж, т.е.:
H=U+рV
U, р, V- функции состояния термодинамической системы, следовательно, «H» - также функция состояния. Таким образом, изменение энтальпии в термодинамическом процессе не зависит от пути процесса и может быть представлена в виде функции двух любых параметров состояния простого тела:
,
где
удельная
энтальпия
h=u+рv,
т.к. рdv=d(рv)-vdр,
тогда dq=d(u+рv)-vdр=dh-vdр,
при р=const,
dq
=dh.
Таким образом элементарное изменение энтальпии:
