Порядок выполнения работы

Упражнение 1. Определение коэффициента вязкости жидкости без учета влияния стенок сосуда.

1. Штангенциркулем измерить диаметр d шарика.

2. Пинцетом или смоченной палочкой опустить шарик по центру сосуда.

3. Определить при помощи секундомера время прохождения шарика между метками.

4. Измерить линейкой расстояние между метками . Повторить пункты 1-3 еще для четырех шариков.

5. Рассчитать коэффициент вязкости по формуле (15.14) в каждом опыте. Плотность жидкостей и плотность шарика взять в приложении.

6. Найти среднее значение коэффициента вязкости и рассчитать погрешность .

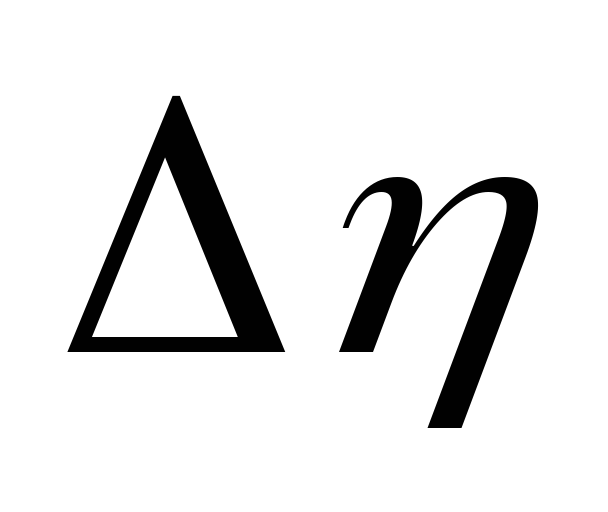Упражнение 2. Определение коэффициента вязкости жидкости по уточненной формуле с учетом влияния стенок сосуда.

1. Измерить линейкой внутренний диаметр 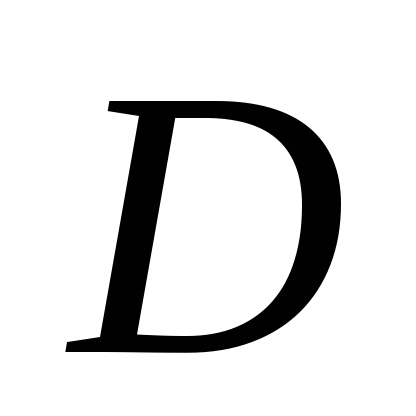сосуда 1.

2. Рассчитать коэффициент вязкости жидкости по формуле (15.15).

3. Сравнить результаты, полученные по формулам (15.14) и (15.15) и сделать выводы.

4. Все результаты занести в таблицу по форме 15.1.

Форма 15.1.

№

d, м

Δd, м

t, c

Δt, c

h, м

Δh, м

η, Па.с

Δηi, Па.с

Δη по (15.17)

D, м

η’, Па.с

l0, м

1

2

3

4

5

Средние

–

–

Замечание. Погрешность коэффициента вязкости Δη рассчитывается двумя способами:

а) по стандартной методике расчета погрешностей случайной величины:

, (15.16)

где коэффициент Стьюдента для числа опытов и доверительной вероятности α=0.95 равен: t_{n, α}=2.57; Δη_i=|η_ср.– η_i|.

б) исходя из формулы (15.14) по стандартной методике расчета погрешностей при косвенных измерениях:

, (15.17)

где , , .

Расчет по (15.17) производится для одного какого-либо опыта, при этом в качестве , и нужно взять приборные погрешности.

Упражнение 3. Оценка участка неравномерного падения шарика l₀.

Выведем формулу для оценки l₀.

Запишем формулу (15.10):

ma=F_тяж–F_Арх–F_С. (15.10)

после подстановки выражений (15.6-15.9) получим:

ρ_шa=(ρ_ш– ρ_ж)g –6πηrv,

или после почленного деления на ρ_ш:

,

и далее после сокращения и элементарных преобразований и с учетом того, что ускорение – это производная скорости по времени :

. (15.18)

Решением дифференциального уравнения (15.18) будет функция:

, (15.19)

где v_р – скорость равномерного (установившегося) движения, v₀ – начальная скорость шарика, которую можно принять равной нулю, коэффициент b в показателе степени экспоненты равен:

. (15.20)

Убедиться в том, что (15.19) является решением уравнения (15.18), можно путем подстановки (15.19) в (15.18), рассчитав предварительно производную скорости v по времени; при этом будут получены также и выражение для b (15.20), и формула для установившейся скорости движения (см.(15.13)):

. (15.21)

Заметим, что (15.19) удовлетворяет начальным условиям: при t=0 скорость равна v₀, при t→∞ скорость v→v_р. Движение можно считать практически равномерным, если экспонента мала:

<<1.

Это реализуется при (bt)→∞, то есть если t>>b^-1. Достаточно потребовать (bt)=4; в этом случае отличие скорости от установившейся составит не более 2% (при v₀=0): . Таким образом, оценим l₀, проинтегрировав (15.19) по времени на промежутке [0: t₁], где :

;

Далее, с учетом того, что и подстановки :

,

откуда с учетом (15.20) и (15.21):

,

и окончательно:

. (15.22)

1. Оценить участок неравномерного движения шарика по формуле (15.22).

2. Записать результат в таблицу 15.1.

3. Сравнить полученное значение с величиной l0, реально используемой в установке.

4. Сделать вывод.

Контрольные вопросы.

1. Запишите формулу Ньютона для коэффициента динамической вязкости. Сделайте поясняющий рисунок.

2. Что называется коэффициентом динамической вязкости? Поясните его физический смысл и выведите его размерность.

3. Объяснить механизм внутреннего трения для газов и жидкостей. Как зависит от температуры вязкость газов и жидкостей? Почему?

4. Какие силы действуют на шарик, падающий в жидкости? Сделайте рисунок, запишите второй закон Ньютона для шарика, падающего в вязкой жидкости.

5. Почему, начиная с некоторого момента, шарик движется равномерно?

6. Как зависит скорость падения шарика от его диаметра?

7. Имеет ли смысл использование уточненной формулы (15.15) при выполнении работы на данной установке?

8. Выведите приближенную расчетную формулу (15.14) для коэффициента вязкости.

9. Докажите (15.19) и (15.20).