
- •Шкала оценки качественных свойств: разновидности, определение, матем. Действия, примеры шкал
- •Шкалы измерения количественных свойств: разновидности, определение, математические действия, примеры шкал.
- •3. Основные требования к системе единиц фв. Примеры систем единиц фв
- •4. Понятие о системных и внесистемных единицах.
- •5. Понятие об основных и производных единицах фв. Выражение производных единиц через основные единицы.
- •7. Экспертный метод оценки качественных свойств фв, схема метода. Критерий согласованности результатов экспертных оценок.
- •8. Основные этапы развития метрологии в России и за рубежом до конца XVIII века.
- •9. Менделеевский период развития метрологии в России
- •Основные метрологические организации рф.
- •Понятие о фв, классификация фв.
- •Классификация величин величины
- •Основные Производные Дополнительные
- •12. Понятие единицы фв. Основное уравнение измерений.
- •13. Понятия об эталонах фв. Классификация эталонов
- •15.Понятие об измерении. Содержание, определения. Необходимое условие измерений.
- •Понятие о передаче размера единицы фв рабочим эталонам. Система поверочных схем.
- •16.Общая классификация измерения
- •17...Классификация измерения по способу получения данных об измеряемой фв. Уравнение соответствующих измерений.
- •18...Общее и отличия между косвенными, совокупными и совместными измерении
- •19. Понятие истинного и действительного значения фв
- •Понятие о погрешностях измерений. Способы выражения погрешности измерений.
- •Относительная погрешность - это погрешность измерения, выраженная отношением абсолютной погрешности измерения () к действительному значению измеряемой величины (хд):
- •21. Понятие отсчёта и принцип арифметического среднего. Основной постулат метрологии: отсчет является случайным числом
- •22. Понятие об оценке рассеяния окончательного результата измерений и оценка рассеивания отдельных результатов измерений хi относительно среднего значения.
- •23. Взаимосвязь между погрешностью и числом измерений.
- •24. Погрешности, подчиняющиеся нормальному закону распределения. Использование дифференциальной и интегральной функции вероятности в определении погрешности измерений.
- •25. Понятие о доверительном интервале и уровне значимости. Роль параметров tp и р в определении погрешностей.
- •26. Доверительный интервал: неравенство Чебышева. Применение критерия.
- •27. Правило «трех сигм» в метрологии
- •28. Семейство распределения Стьюдента в метрологии.
- •29. Понятие о систематических погрешностях. Общая классификация.
- •30. Выявление и исключение систематических погрешностей методом серий.
- •31. Выявление и исключение систематических погрешностей дисперсным методом.
- •32. Основные методы выявления и исключения грубых погрешностей.
- •33. Средства измерений (си) – определение, классификация.
- •Мх си. Основные нормированные мх
- •36. Понятие класса точности си. Способы назначения классов точности си
- •37. Способы обозначения классов точности си
- •38. Алгоритм обработки многократных равноточных измерений.
- •39. Метод проверки нормального распределения погрешности измерений (критерий Пирсона)
- •40. Алгоритм обработки результатов неравноточных измерений.
- •41. Алгоритм обработки результатов косвенных измерений.
- •42. Метод коэффициентов, как способ приближенного определения погрешностей косвенных измерений.
- •43. Закон рф «о техническом регулировании» и задачи обеспечения единства измерений.
- •44. Ответственность за нарушение законодательства по метрологии
- •45. Система испытаний и утверждения типа си.
- •46. Понятие о поверке си. Основные документы, регламентирующие поверочную деятельность. Классификация поверок си
- •Понятие о калибровке си. Область применения. Российская система калибровки.
- •Международные организации по метрологии.
- •50. Понятие о стандартизации, ее сущность и содержание.
- •51. Закон рф «о техническом регулировании» и задачи обеспечения единства измерений.
- •59. Ряды предпочтительных чисел r5, r10, r20, r40. Взаимосвязь предпочтительных чисел в данном ряду.
- •60. Ряды предпочтительных чисел r5, r10, r20, r40. Логарифмическое правило.
- •61. Ряды предпочтительных чисел, построенные на базе геометрической прогрессии: правило перехода из одного десятичного интервала в другой.
31. Выявление и исключение систематических погрешностей дисперсным методом.
В практике измерений часто бывает необходимо выяснить наличие систематических погрешности результатов наблюдений, обусловленной влиянием какого-либо фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. С этой целью проводят многократные измерения, состоящие из и достаточного числа серий, каждая из которых соответствует определенным значениям влияющего фактора (ими могут быть внешние условие – температура, давление, или временная последовательность измерений и т.п.).
Выявление систематических погрешностей с помощью дисперсионного анализа (универсальный метод Фишера).
Проведено N измерений, разбиваем на s серий (s>3) по nj в каждой серии. snj= N. Определяем имеется или отсутствует систематическое расхождение.
Характеристикой совокупности случайных внутрисерийных погрешностей будет ср сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии.
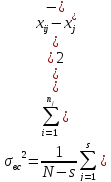
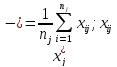 -
результат i-того
измерения в j-той
серии.
-
результат i-того
измерения в j-той
серии.
Внутрисерийная
дисперсия
 хар-т случайные погр измерений. Далее
рассчитывается усредненная межсерийная
дисперсия.
хар-т случайные погр измерений. Далее
рассчитывается усредненная межсерийная
дисперсия.
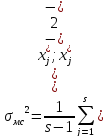 -
выражает силу действия фактора,
вызывающего систематические различия
между сериями.
-
выражает силу действия фактора,
вызывающего систематические различия
между сериями.
Т.о.
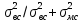 -
коэффициент
ошибки
- харак-т долю дисперсии всех результатов
наблюдений, обусловленную наличием
случайных погрегностей измерений, а
-
коэффициент
ошибки
- харак-т долю дисперсии всех результатов
наблюдений, обусловленную наличием
случайных погрегностей измерений, а
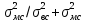 - показатель
дифференциации
– долю дисперсии, обусловленную
межсирийными различиями результатов
наблюдений. Чем больше отнашение
показателя дифференциации к коэффициенту
ошибки, тем сильнее действие фактора,
по которому группировались серии и тем
больше систематическое различие между
ними.
- показатель
дифференциации
– долю дисперсии, обусловленную
межсирийными различиями результатов
наблюдений. Чем больше отнашение
показателя дифференциации к коэффициенту
ошибки, тем сильнее действие фактора,
по которому группировались серии и тем
больше систематическое различие между
ними.
Критерий оценки наличия сист погр явл дисперсиооный критерий Фишера F=62мс/62вс. Критическая область для критерия Фишера соответствует Р(F >Fq)=q.
Значение Fq для различных уровней значимости q, числа и змерений N и числа серий s представляют собой табличные данные, где даются степени свободы k2=N-s, k1=s-1. Если полученное знач критерия Фишера больше, то обнар сист погрешность.
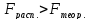 -
это
есть систематическая ошибка.
-
это
есть систематическая ошибка.
32. Основные методы выявления и исключения грубых погрешностей.
Грубая
погрешность или промах – это погрешность
отдельного результата измерения,
входящего в ряд измерений, которая для
данных условий резко отличается от
остальных результатов этого ряда.
Грубые
погрешности измерений (промахи) могут
сильно исказить
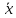 ,
и доверительный интервал, поэтому их
исключение из серии измерений обязательно.
Обычно в ряду полученных результатов
они сразу видны, но в каждом конкретном
случае это необходимо доказать.
Существует ряд критериев для оценки
промахов.
,
и доверительный интервал, поэтому их
исключение из серии измерений обязательно.
Обычно в ряду полученных результатов
они сразу видны, но в каждом конкретном
случае это необходимо доказать.
Существует ряд критериев для оценки
промахов.
Критерий З. В этом случае считается, что результат, возникающий с вероятностью Р < 0,003, нереален и его можно рассматривать как промах, т. е. сомнительный результата отбрасывается, если
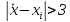
Величины
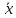 ,
и
и вычисляют без учета хi
.
Данный критерий надежен при числе
измерений п
> 20,.
..,50.
,
и
и вычисляют без учета хi
.
Данный критерий надежен при числе
измерений п
> 20,.
..,50.
Если 4 < п < 20, применяют критерий Романовского.
В соответствии с данным критерием вычисляют отношение:
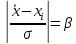
и полученное значение сравнивают с теоретическим т — при выбираемом уровне значимости Р по таблице.
Уровень значимости Т = f(п)
Обычно выбирают Р = 0,01-0,05. Если т , то результат отбрасывают.
Критерий
Шовине
можно применять, если число измерений
невилико – не превышает 10, т.е есть
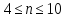 . в этом случае промахом считается
результат xi,
если в зависимости от числа измерений
n
разность
. в этом случае промахом считается
результат xi,
если в зависимости от числа измерений
n
разность
 превышает число сигм:
превышает число сигм:
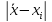
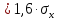 ,
при n
= 4;
,
при n
= 4;
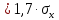 ,
при n
= 6;
,
при n
= 6;
 ,
при n
= 8;
,
при n
= 8;
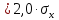 ,
при n
= 10;
,
при n
= 10;
