
- •Дифференциальное исчисление
- •Содержание
- •Введение
- •Задачи для самостоятельного решения
- •Свойства бесконечно малых и бесконечно больших функций
- •Теоремы о пределах (правила предельного перехода)
- •Замечательные пределы. Сравнение бесконечно малых величин
- •Задачи для самостоятельного решения
- •Свойства эквивалентных бесконечно малых функций
- •Важнейшие эквивалентности
- •Задачи для самостоятельного решения
- •3. Практическое занятие по теме: Непрерывность функции. Точки разрыва и их классификация
- •Задачи для самостоятельного решения
- •4. Практическое занятие по теме: вычисление производной функции одной переменной. Таблица производных. Нахождение частных производных. Производная сложной функции
- •Правила дифференцирования результатов арифметических действий над функциями
- •Геометрический смысл производной функции одной переменной
- •Геометрический смысл частных производных функции двух переменных
- •Задачи для самостоятельного решения
- •5. Практическое занятие по теме: производная неявной функции однОй и нескольких переменных. Производная функции, заданной параметрически. Логарифмическое дифференцирование
- •Производная неявно заданной функции.
- •Производная функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Задачи для самостоятельного решения
- •6. Практическое занятие по теме: Дифференциал функции одной и нескольких переменных, применение дифференциалов в приближенных вычислениях. Производные и дифференциалы высших порядков
- •Основные свойства дифференциала
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •7. Практическое занятие по теме: Правило Лопиталя
- •1.Неопределенность
- •2.Неопределенность .
- •3.Неопределенности , , .
- •Задачи для самостоятельного решения
- •8. Практическое занятие по теме: Общая схема исследования функции и построение графика
- •Алгоритм исследования функции
- •Задачи для самостоятельного решения
- •Библиографический список
Задачи для самостоятельного решения
Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию:
3.1.![]()
3.2.
![]()
3.3.
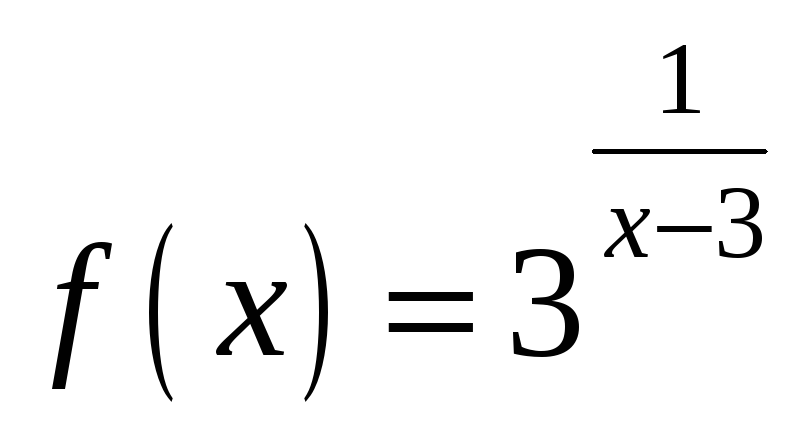
3.4.

3.5.
![]()
3.6.

3.7.

3.8.
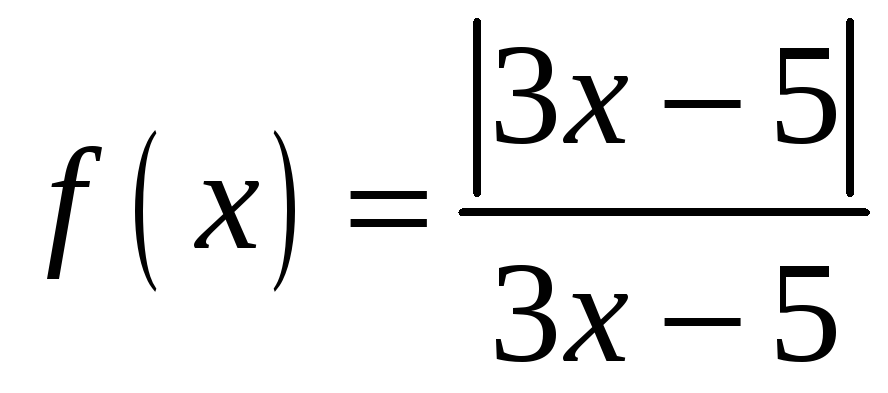
3.9.
![]()
3.10.
![]()
3.11.

3.12.
![]()
3.13.
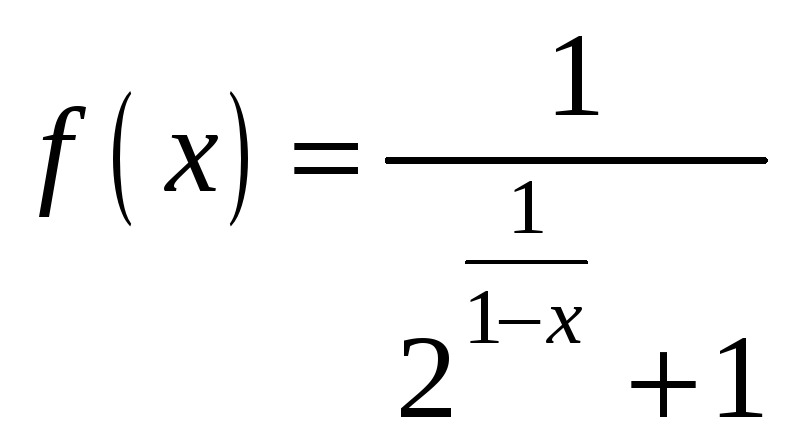
3.14.

3.15.
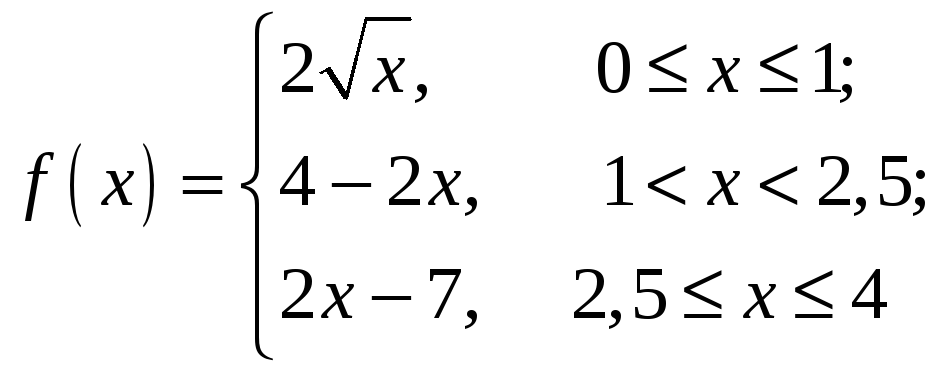
3.16.

3.17.

Задана функция
![]() .
При каком выборе параметров, функция
.
При каком выборе параметров, функция
![]() будет непрерывной?
будет непрерывной?
3.18.
3.19.
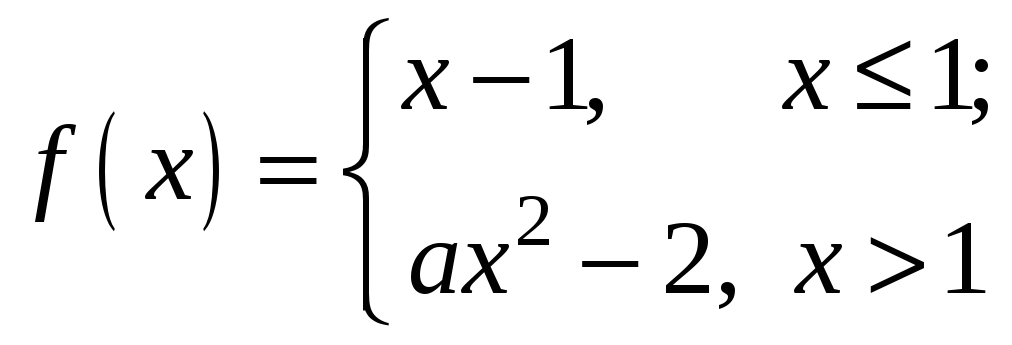
3.20.
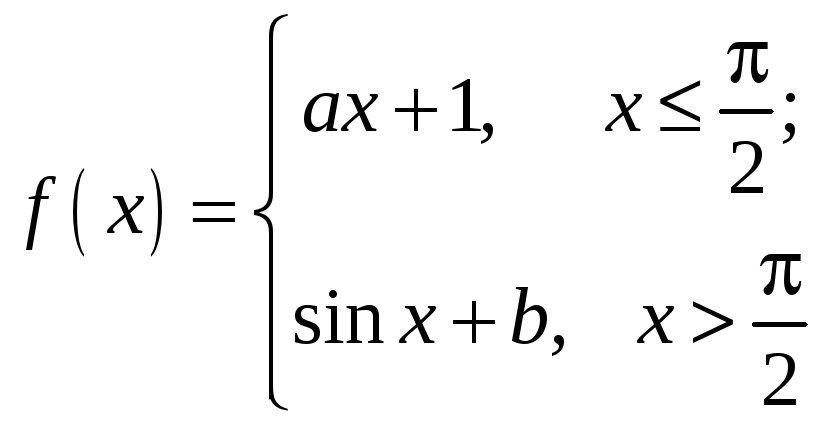
4. Практическое занятие по теме: вычисление производной функции одной переменной. Таблица производных. Нахождение частных производных. Производная сложной функции
Определение 1.
Производной
функции одной переменной
![]() в точке
в точке
![]() называется
предел отношения приращения функции
к приращению независимой переменной
этой точки, при стремлении последнего
к нулю.
называется
предел отношения приращения функции
к приращению независимой переменной
этой точки, при стремлении последнего
к нулю.
Обозначается
![]() .
.
 (4.1)
(4.1)
Операция нахождения производной называется дифференцированием.
Теорема 1.
Если функция
![]() имеет производную
имеет производную
![]() в точке
в точке
![]() ,
функция
,
функция
![]() имеет производную
имеет производную
![]() в соответствующей точке
в соответствующей точке
![]() (
(![]() ),
то сложная функция
),
то сложная функция
![]() имеет производную
имеет производную
![]() ,
в точке
,
в точке
![]() ,
которая находится по формуле
,
которая находится по формуле
![]() .
.
Правила дифференцирования результатов арифметических действий над функциями
Пусть
![]() ,
,
![]() ,
,
![]() .
.
-
 ,
где
,
где

-
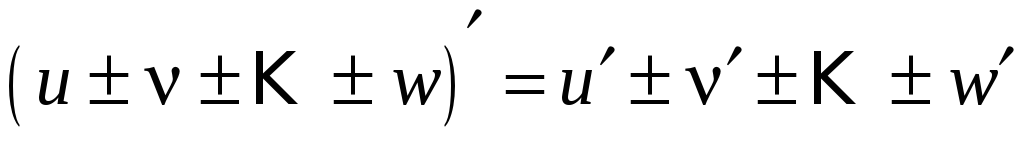
-

-

-

![]()
-
 ,
где
,
где
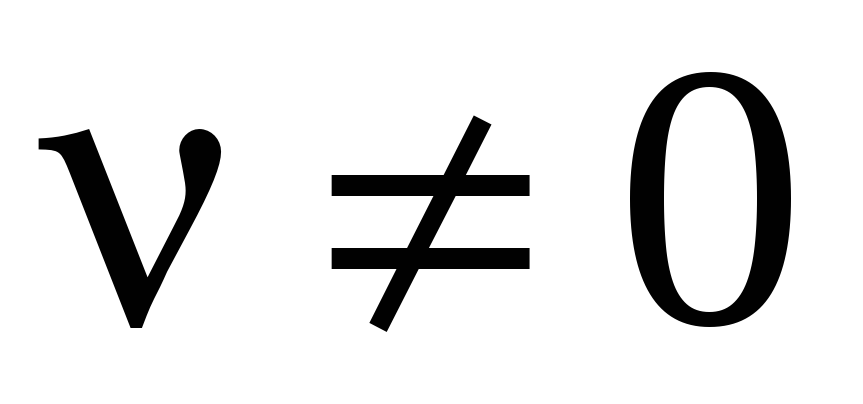
ТАБЛИЦА ПРОИЗВОДНЫХ
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Геометрический смысл производной функции одной переменной
![]()
 ,
где
,
где
![]() ‑ угол между осью
‑ угол между осью
![]() и касательной, проведенной к графику
функции
и касательной, проведенной к графику
функции
![]() в точке
в точке
![]() ,
,
![]() ‑ угловой коэффициент касательной
(см. рис.4.1).
‑ угловой коэффициент касательной
(см. рис.4.1).
-
уравнение касательной:
![]() ; (4.2)
; (4.2)
-
уравнение нормали:
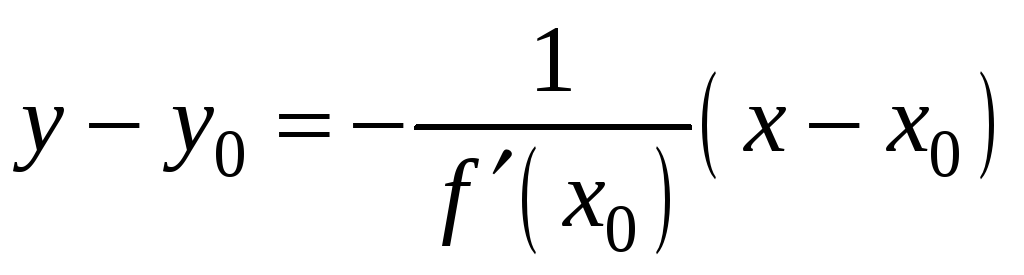 (если
(если
![]() ).(4.3)
).(4.3)
Пример 1.
Используя определение производной,
найти производную функции
![]() .
.
Решение. 1.
По приращению независимой переменной
![]() находим приращение функции
находим приращение функции
![]() ,
имеем
,
имеем
![]() .
.
2. Составляем
отношение
![]() ,
имеем
,
имеем
 .
.
3. По формуле (4.1)

Так как
![]() при
при
![]() (см. п.2, важнейшие эквивалентности), то
(см. п.2, важнейшие эквивалентности), то
 ,
тогда
,
тогда
![]() .
.
Ответ.
![]() .
.
Пример 2. Найти производные функций.
а)
![]() .
.
Решение. По правилу 5 находим
 .
.
Ответ.
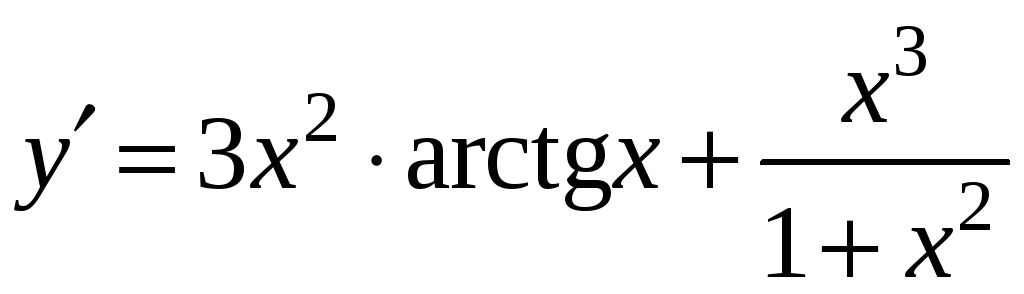 .
.
б)
![]() .
.
Решение. Обозначим
![]() ,
тогда
,
тогда
![]() .
Используя теорему
1 о дифференцировании сложной функции
и формулы 2 и 10 таблицы производных
имеем:
.
Используя теорему
1 о дифференцировании сложной функции
и формулы 2 и 10 таблицы производных
имеем:
![]() .
.
Ответ.
![]() .
.
в)
![]() .
.
Решение. Обозначим
![]() ,
тогда
,
тогда
![]() .
Используя теорему 1 о дифференцировании
сложной функции одной переменной и
формулу 5 таблицы производных, имеем:
.
Используя теорему 1 о дифференцировании
сложной функции одной переменной и
формулу 5 таблицы производных, имеем:
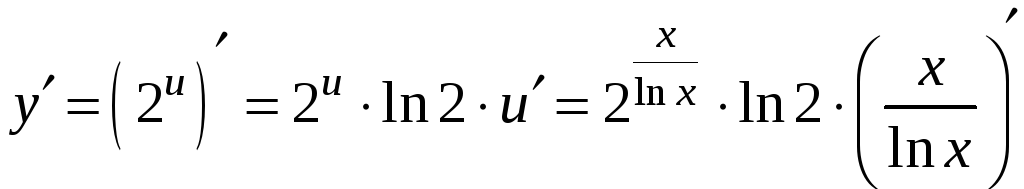 .
По правилу 6 находим
.
По правилу 6 находим
 ,
тогда
,
тогда
 .
.
Ответ.
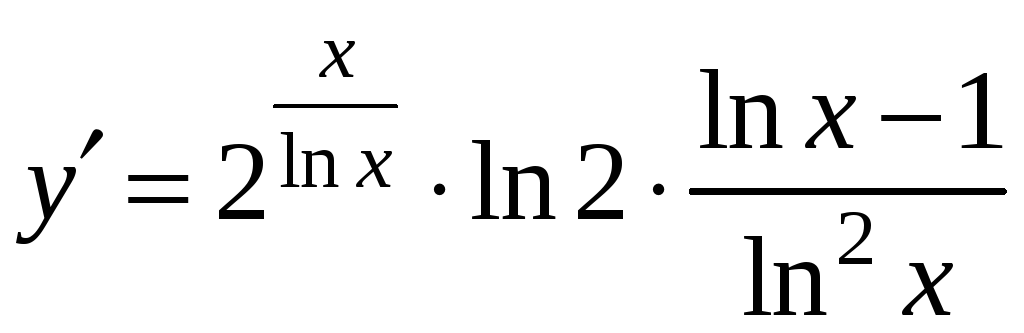 .
.
Пример 3.
Составить уравнения касательной и
нормали к графику функции
![]() в точке с абсциссой
в точке с абсциссой
![]() .
.
Решение.
Если
![]() ,
то
,
то
![]() ,
а
,
а
![]() и
и
![]() .
По формулам (4.2.) и (4.3) уравнение касательной
примет вид
.
По формулам (4.2.) и (4.3) уравнение касательной
примет вид
![]() ,
,
![]() ,
,
![]() ,
а уравнение нормали – соответственно
,
а уравнение нормали – соответственно
![]() ,
,
![]() ,
,
![]() .
.
Ответ. Уравнение
касательной
![]() ,
,
уравнение нормали
![]() .
.
Пример 4.
Найти угол между линиями
![]() и
и
![]() .
.
Решение. Угол между линиями ‑ это угол между касательными к этим линиям, проведенными к каждой из них в точке их пересечения.
Найдем точки
пересечения заданных линий:
![]() ,
,
![]() .
Теперь найдем угловые коэффициенты
касательных к этим линиям в каждой
точке пересечения:
.
Теперь найдем угловые коэффициенты
касательных к этим линиям в каждой
точке пересечения:
 ,
,
 ,
,
при
![]()
![]() ;
;
![]() ,
,
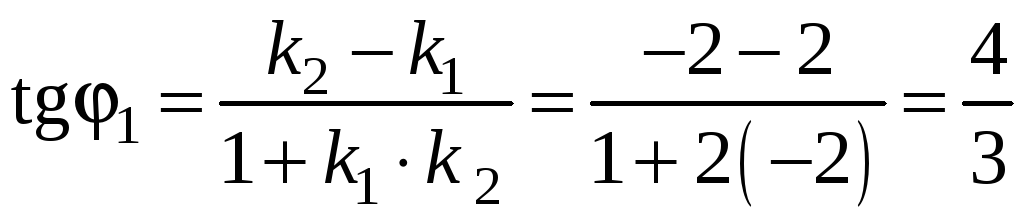 ;
;
![]() ;
;
при
![]()
![]() ;
;
![]() ,
,
![]() ;
;
 .
.
Ответ.
![]() ,
,
 .
.
Определение 2.
Частной
производной функции двух переменных
![]() в точке
в точке
![]() по данной независимой переменной
называется предел отношения приращения
функции в точке
по данной независимой переменной
называется предел отношения приращения
функции в точке
![]() к соответствующему приращению независимой
переменной, при стремлении последнего
к нулю. Обозначается
к соответствующему приращению независимой
переменной, при стремлении последнего
к нулю. Обозначается
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
![]() ;
;
 . (4.4)
. (4.4)
Аналогично для
функции
![]() ‑ независимых переменных
‑ независимых переменных
![]() :
:
 .
.
Из определения частных производных следует, что частная производная находится в предположении, что изменяется только одна независимая переменная, а остальные остаются постоянными.
Теорема 2.
Если
![]() ‑ дифференцируемая функция и
‑ дифференцируемая функция и
![]() ,
,
![]() ‑ дифференцируемые функции независимых
переменных
‑ дифференцируемые функции независимых
переменных
![]() и
и
![]() ,
то производные сложной функции
,
то производные сложной функции
![]() по каждой независимой переменной
по каждой независимой переменной
![]() и
и
![]() вычисляются по формулам:
вычисляются по формулам:
![]() ,
,
 . (4.5)
. (4.5)
Теорема 3.
Если
![]() дифференцируемая функция и
дифференцируемая функция и
![]() ,
,
![]() дифференцируемые функции независимой
переменной
дифференцируемые функции независимой
переменной
![]() ,
то производная сложной функции
,
то производная сложной функции
![]() вычисляется
по формуле
вычисляется
по формуле
 . (4.6)
. (4.6)
Следствие. Если
![]() дифференцируемая функция и
дифференцируемая функция и
![]() ‑ дифференцируемая функция независимой
переменной
‑ дифференцируемая функция независимой
переменной
![]() ,
то производная сложной функции
,
то производная сложной функции
![]() вычисляется по формуле
вычисляется по формуле
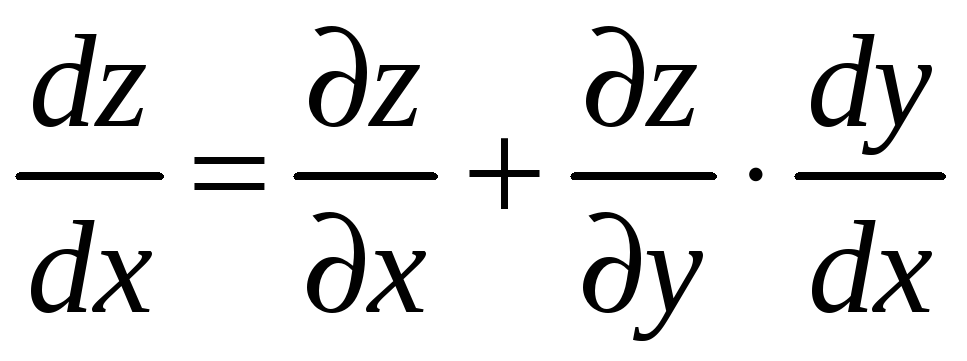 . (4.7)
. (4.7)




