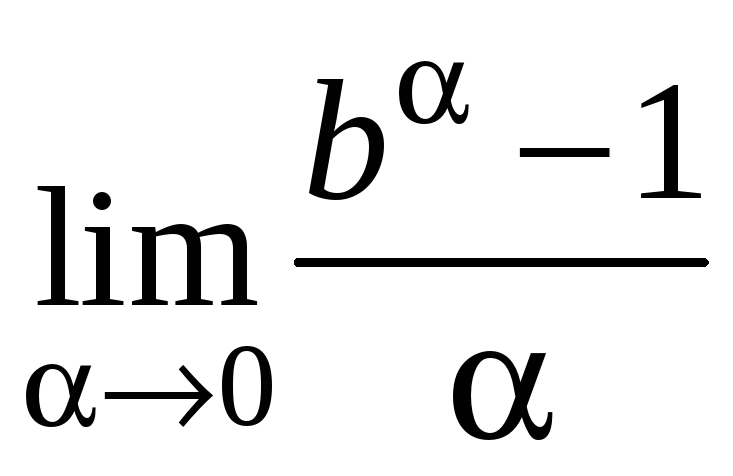- •Дифференциальное исчисление
- •Содержание
- •Введение
- •Задачи для самостоятельного решения
- •Свойства бесконечно малых и бесконечно больших функций
- •Теоремы о пределах (правила предельного перехода)
- •Замечательные пределы. Сравнение бесконечно малых величин
- •Задачи для самостоятельного решения
- •Свойства эквивалентных бесконечно малых функций
- •Важнейшие эквивалентности
- •Задачи для самостоятельного решения
- •3. Практическое занятие по теме: Непрерывность функции. Точки разрыва и их классификация
- •Задачи для самостоятельного решения
- •4. Практическое занятие по теме: вычисление производной функции одной переменной. Таблица производных. Нахождение частных производных. Производная сложной функции
- •Правила дифференцирования результатов арифметических действий над функциями
- •Геометрический смысл производной функции одной переменной
- •Геометрический смысл частных производных функции двух переменных
- •Задачи для самостоятельного решения
- •5. Практическое занятие по теме: производная неявной функции однОй и нескольких переменных. Производная функции, заданной параметрически. Логарифмическое дифференцирование
- •Производная неявно заданной функции.
- •Производная функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Задачи для самостоятельного решения
- •6. Практическое занятие по теме: Дифференциал функции одной и нескольких переменных, применение дифференциалов в приближенных вычислениях. Производные и дифференциалы высших порядков
- •Основные свойства дифференциала
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •7. Практическое занятие по теме: Правило Лопиталя
- •1.Неопределенность
- •2.Неопределенность .
- •3.Неопределенности , , .
- •Задачи для самостоятельного решения
- •8. Практическое занятие по теме: Общая схема исследования функции и построение графика
- •Алгоритм исследования функции
- •Задачи для самостоятельного решения
- •Библиографический список
Свойства эквивалентных бесконечно малых функций
![]() Предел отношения
двух бесконечно малых функций не
изменится, если каждую или одну из них
заменить эквивалентной ей бесконечно
малой:
Предел отношения
двух бесконечно малых функций не
изменится, если каждую или одну из них
заменить эквивалентной ей бесконечно
малой:
 ,
где
,
где
![]() ,
,
![]() .
.
![]() Разность двух
эквивалентных бесконечно малых функций
есть бесконечно малая более высокого
порядка, чем каждая из них.
Разность двух
эквивалентных бесконечно малых функций
есть бесконечно малая более высокого
порядка, чем каждая из них.
![]() Сумма конечного
числа бесконечно малых функций разных
порядков эквивалентна слагаемому
низшего порядка.
Сумма конечного
числа бесконечно малых функций разных
порядков эквивалентна слагаемому
низшего порядка.
Для раскрытия
неопределенностей вида
![]() часто бывает полезным применять принцип
замены бесконечно малых эквивалентными
и другие свойства эквивалентных
бесконечно малых функций.
часто бывает полезным применять принцип
замены бесконечно малых эквивалентными
и другие свойства эквивалентных
бесконечно малых функций.
Важнейшие эквивалентности
при
![]()
|
1.
|
6.
|
|
2.
|
7.
|
|
3.
|
8.
|
|
4.
|
9.
|
|
5.
|
10.
в
частности,
|
Пример 9.
Сравнить бесконечно малые
![]() и
и
![]() (
(![]() ).
).
Решение. Найдем
 .
Используя важнейшие эквивалентности,
при
.
Используя важнейшие эквивалентности,
при
![]() имеем
имеем
![]() ,
,
![]() .
.
Поэтому
 .
Значит
.
Значит
![]() бесконечно малая более высокого порядка
малости.
бесконечно малая более высокого порядка
малости.
Пример 10.
Сравнить бесконечно малые
![]() и
и
![]() (
(![]() ).
).
Решение. Найдем
 .
Значит
.
Значит
![]() и
и
![]() одного порядка малости, более того, они
эквивалентны, т.е
одного порядка малости, более того, они
эквивалентны, т.е
![]() .
.
Пример 11.
Определить порядок относительно
![]() функции
функции
![]() бесконечно
малой при
бесконечно
малой при
![]() .
.
а)
 .
.
Решение. Требуется
найти число
![]() такое, чтобы
такое, чтобы
 .
Имеем
.
Имеем
 .
.
При
![]()
![]() ,
что не подходит,
,
что не подходит,
при
![]()
![]() ,
т.е.
,
т.е.
при
![]()
 .
.
Итак,
![]() и
и
 ,
при
,
при
![]() .
.
б)
![]() .
.
Решение. Требуется
найти число
![]() такое, чтобы
такое, чтобы
 .
.
Используя важнейшие
эквивалентности, при
![]() имеем
имеем
 .
.
Поэтому
 ,
а
,
а

Т.е. при
![]()
 .
Итак,
.
Итак,
![]() и функция
и функция
![]() ‑ бесконечно малая третьего порядка
малости относительно бесконечно малой
‑ бесконечно малая третьего порядка
малости относительно бесконечно малой
![]() при
при
![]() .
.
Пример 12. С помощью замены эквивалентных найти пределы.
а)
 .
.
Решение. Используя
важнейшие эквивалентности, при
![]() имеем
имеем
![]() ,
,
![]() .
.
Поэтому
 .
.
Ответ.
 .
.
б)
![]() .
.
Решение. Перейдем
к новой переменной
![]() ,
тогда
,
тогда
![]() и
при
и
при
![]() ,
,
![]() .
Получаем
.
Получаем
 .
Преобразуем выражение, стоящее в
числителе:
.
Преобразуем выражение, стоящее в
числителе:
 .
.
Используя важнейшие
эквивалентности, имеем при
![]()
 .
.
Поэтому
 .
.
Ответ.
![]() .
.
в)
 .
.
Решение. Преобразуем выражение, стоящее в числителе:
![]() .
.
Тогда
 .
.
Используя важнейшие
эквивалентности, имеем при
![]()
 ,
,
![]() ,
,
![]() .
.
Поэтому
 .
.
Ответ.
 .
.
г)
 .
.
Решение. Преобразуем выражение, стоящее в скобках:
 .
.
При
![]()
![]() ,
тогда, используя важнейшие эквивалентности,
имеем при
,
тогда, используя важнейшие эквивалентности,
имеем при
![]()
 .
.
Поэтому
 .
.
Ответ.
 .
.
Задачи для самостоятельного решения
2.27. Убедиться, что
при
![]()
![]() и
и
![]() одного порядка малости. Будут ли они
эквивалентными?
одного порядка малости. Будут ли они
эквивалентными?
2.28. Сравнить
бесконечно малые
![]() и
и
![]() (
(![]() ).
).
2.29. Сравнить
бесконечно малые
![]() и
и
![]() (
(![]() ).
).
2.30. Определить
порядок относительно
![]() функции, бесконечно малой при
функции, бесконечно малой при
![]() :
1)
:
1)![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() .
.
С помощью замены эквивалентных найти пределы.
2.31.

2.32.

2.33.

2.34.
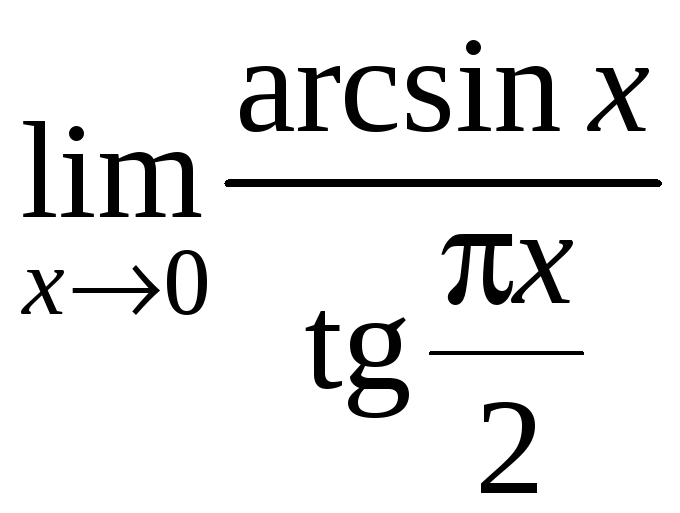
2.35.
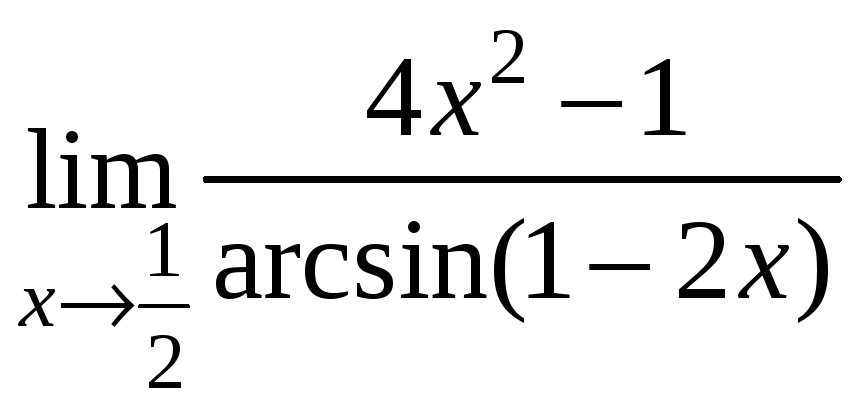
2.36.

2.37.

2.38.
![]()
2.39.
![]()
2.40.

2.41.

2.42.

2.43.
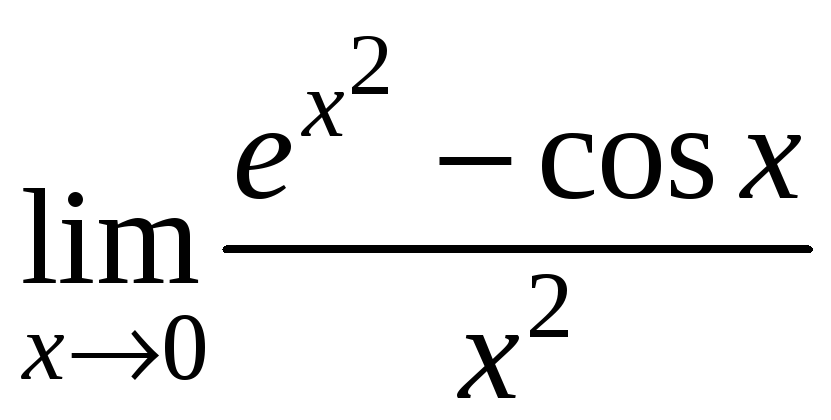
2.44.

2.45.