Замечательные пределы. Сравнение бесконечно малых величин
Первый замечательный предел
. (2.1)
Второй замечательный предел
, (2.2)
. (2.3)
Число
называется неперовым
числом,
.
Следствия замечательных пределов
, (2.4)
, (2.5)
, (2.6)
, (2.7)
, (2.8)
где
,
при
.
Пример 1. Найти
предел
.
Решение. Перейдем
к новой переменной
,
тогда
.
Теперь при
,
получаем
,
т.к. по формуле (2.4)
.
Ответ.
.
Пример 2.
Найти предел
.
Решение. Умножим
и разделим выражение, стоящее под знаком
предела на
:
.
Тогда
.
По формуле (2.5)
,
.
Тогда
.
Ответ.
.
Пример 3.
Найти предел
.
Решение.
,
тогда
т.к. по формуле
(2.1)
,
по формуле (2.5)
и
.
Ответ.
.
Пример 4.
Найти предел
Решение. Перейдем
к новой переменной
.
Тогда
,
,
и при
,
поэтому получаем
.
Так как
,
то
по формуле (2.1),
а
,
тогда
Ответ.
.
Пример 5.
Найти предел
.
Решение.
При
в данном пределе имеем неопределенность
.
Тогда по формуле
(2.7)
.
Ответ.
.
Пример 6.
Найти предел
.
Решение.
,
т.к.
(см.
п.1).
.
Таким образом, в
данном пределе имеем неопределенность
.
Преобразуем выражение, стоящее в
скобках:
.
Тогда
,
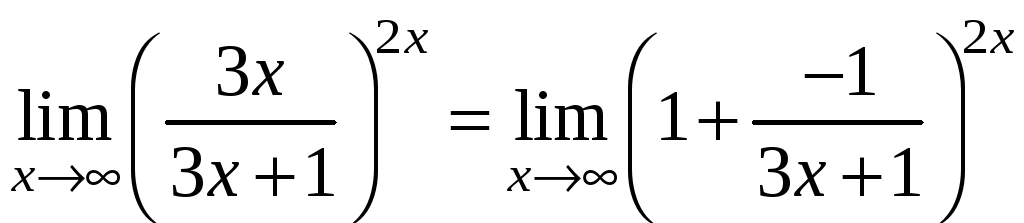где
,
при
.
Воспользуемся формулой (2.8):
.
Здесь
,
т.к.
(см. п.1).
Ответ.
.
Пример 7.
Найти предел
.
Решение.
,
,
т.к. при
‑ бесконечно малая функция, а значит
‑ бесконечно большая (см. п.1).
Поэтому
в данном пределе имеем неопределенность
.
Перейдем к новой переменной
.
Тогда
:
.
При
.
Получаем:
,
где
,
а
при
.
Воспользуемся формулой (2.8):
.
Ответ.
.
Пример 8.
Найти предел
.
Решение.
Преобразуем
выражения, стоящие в скобках и в
показателе степени:
,
.
Тогда
,
где
и
при
.
Воспользуемся формулой (2.8):
Ответ.
.
Задачи для самостоятельного решения
Найти пределы.
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
2.11.
2.12.
2.13.
2.14.
2.15.
2.16. .
2.17.
2.18.
2.19.
2.20.
2.21.
2.22.
2.23.
2.24.
2.25.
2.26.
При приближении к предельной точке, общей для нескольких бесконечно малых функций, скорость их стремления к нулю бывает различной. Сравнение таких бесконечно малых функций привело к понятию порядка малости.
Если
,
то
– бесконечно малая
–го
порядка малости относительно
.
Чем выше порядок малости, тем быстрее переменная стремится к нулю.
Чтобы сравнить две бесконечно малые функции надо найти предел их отношения.
Пусть
и
есть бесконечно малые функции при
,
т. е.
и
.
Если
Отметим, что таковы
же правила сравнения бесконечно малых
функций при
.
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые функции.
Бесконечно малые
функции
и
называются эквивалентными
при
,
если
;
это обозначается так:
.